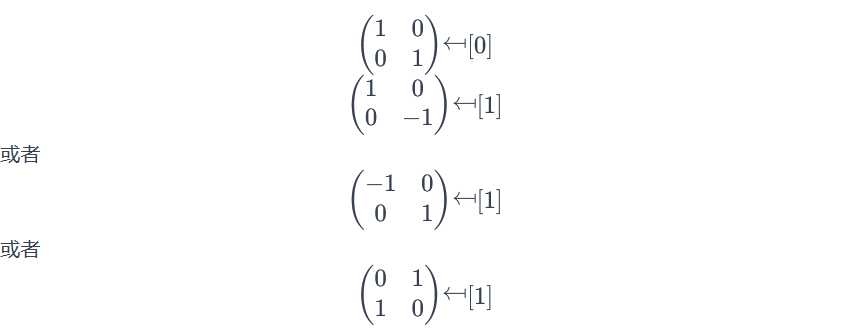半直积

在上述例子中，显然无法将 $\mathbb{Z}/n\mathbb{Z}$ 视为 $\mathbb{Z}$ 的子群。

因此我们有了一个新的想法。我们希望能够在自然地认出半直积，并且希望能够产生例子！让我们分析一下。

如前所述，在分裂短正合序列中让我们将 $R$ 与 $j(R)$ 识别。那么，$R$ 的每一个元素都通过共轭在 $H$ 本身上定义了一个作用：$h\mapsto rhr^{-1}$。由于 $L$ 是正规子群，$rLr^{-1}=L$，因此这在 $L$ 上定义了一个通过 $C_{r}: l\mapsto rlr^{-1}$ 的作用。

此外，这从 $L$ 到其自身是一个群同构。我们可以证明，这定义了一个从 $R$ 到 $\mathrm{Aut}(L)$ 的群同态，给定 $r\mapsto C_{r}$。换句话说，证明 $C_{r}\circ C_{r^{\prime}}=C_{rr^{\prime}}$ 是等价的，因为对于 $h\in R$，我们有$$(C_{r}\circ C_{r^{\prime}})(h)=C_{r}(C_{r^{\prime}}(h))=C_{r}(r^{\prime}hr^{\prime -1})=r(r^{\prime}hr^{\prime -1})r^{-1}.$$利用群运算的结合律，这可以简化为$$(C_{r}\circ C_{r^{\prime}})(h)=(rr^{\prime})h(rr^{\prime})^{-1}=C_{rr^{\prime}}(h).$$这个新的映射 $R\to \mathrm{Aut}(L)$ 被称为 $R$ 在 $L$ 上的共轭作用(conjugation action)。因此，任何分裂都会产生一个从 $R$ 到 $\mathrm{Aut}(L)$ 的群同态。(这里的 $\mathrm{Aut}(L)$ 指的是群的自同构群，而不是集合的自同构群。)

问题：确定两个群 $R$ 和 $L$。自然的问题是：任何从 $R\to\mathrm{Aut}(L)$ 的群同态是否会产生一个分裂正合序列？

另一个观察是，给定一个分裂，$R$ 和 $L$ 都变成了 $H$ 的子群。此外，它们的交集只包含 $1_{H}$——毕竟，如果非单位元 $l\in L\cap R$，那么映射 $R\to H\to R$ 就不可能是单射（$l$ 会在 $R$ 的像中，从而在 $H\to L$ 的核中）。最后，由于 $L$ 作用的轨道覆盖了整个 $H$，我们得到 $H=\bigcup\limits_{r\in R}Lr$。即 $H=LR$。

定义 设 $L$，$R$ 为 $H$ 的子群。我们定义$$LR={g~\text{使得}~g=lr~\text{对于某些}~l\in L, r\in R}.$$

为了证明在短完全序列 $L\to H\to R$ 分裂时 $H=LR$，我们需要以下引理。

引理 设 $L\to H\xrightarrow{\psi} R$ 为一个短正合序列。设 $q: H\to H/L$ 为商同态，发送 $h\mapsto Lh$。则存在一个同构 $z: H/L\to R$ 使得 $z\circ q=\psi$。（即存在 $z$ 使得如下图

是交换的。）证明：我们已知短正合序列 $L \to H \xrightarrow{\psi} R$，其中 $\psi: H \to R$ 是满射，其核为 $L$。我们想证明存在同构 $z: H/L \to R$ 使得 $z \circ q = \psi$，其中 $q: H \to H/L$ 是商映射。由于 $\psi$ 是满射且 $\ker(\psi) = L$，根据第一同构定理，我们知道：$$H / L \cong R.$$定义一个从 $H/L \to R$ 的映射 $z$：$$z(Lh) = \psi(h).$$这是良定义的，因为如果 $Lh_1 = Lh_2$，那么 $h_1 h_2^{-1} \in L = \ker(\psi)$，所以 $\psi(h_1) = \psi(h_2)$。$z$ 是一个同构，因为：- $z$ 是同态，因为 $\psi$ 是同态。- $z$ 是满射，因为 $\psi$ 是满射。- $z$ 是单射，因为 $z$ 的核正是 $L$，意味着唯一被映射到 $R$ 中单位元的是 $L$。对于所有 $h \in H$，$(z \circ q)(h) = z(Lh) = \psi(h)$，所以 $z \circ q = \psi$。因此，$z$ 是使得图表交换的所需同构。根据第一同构定理，存在一个同构 $z: H/L \to R$ 使得 $z \circ q = \psi$，证明了引理。

$$~\tag*{$\square$}$$

一旦我们有了这个引理，我们可以证明以下推论：

推论 如果 $j: R\to H$ 是 $L\to H\to R$ 的一个分裂，则$$H=\bigcup\limits_{r\in R} Lj(r).$$

证明：根据分裂的定义，我们有 $\psi\circ j=\mathrm{id}_{R}$。另一方面，根据引理，我们知道 $\psi=z\circ q$，所以我们有

$$z\circ q\circ j=\mathrm{id}_{R}。$$

由于 $z$ 是一个群同构，其逆映射是一个同态，我们有同态的等式

$$q\circ j=z^{-1}。$$

现在我们解释映射 $q\circ j$。同态 $q$ 将 $h$ 映射到 $Lh$。因此复合映射 $q\circ j$ 将 $r$ 发送到商集 $Lj(r)\in H/L$。而 $z^{-1}$ 是到 $H/L$ 的双射，所以对于 $H/L$ 中的任何商集 $Lh$，我们有一个唯一的 $r\in R$，使得 $Lh=Lj(r)$。因为

$$\bigcup\limits_{H/L} Lh=H,$$

这就证明了

$$\bigcup\limits_{r\in R} Lj(r)=H.$$

$$~\tag*{$\square$}$$

在上面的注释中，我们使用 $j$ 将 $r\in R$ 与它在 $H$ 中的像进行了识别，因此我们将其写作

$$\bigcup\limits_{r\in R}Lr=H.$$

问题：确定 $L, R\subset H$。如果 $L\cap R={1}$，$L\subset H$ 是正规子群且 $LR=H$，那么 $H$ 是否是 $L$ 和 $R$ 的半直积？

我们问的问题真是好问题，因为答案是肯定的！

定理* 确定一个正规子群 $L\subset H$，并设 $R\cong H/L$。以下条件等价：

(1) 一个同态 $j: R\to H$ 将短正合序列 $L\to H\to R$ 分裂。

(2) 一个到子群 $R^{\prime}\subset H$ 的同构 $R\to R^{\prime}$，使得 $R^{\prime}\cap L={1}$ 且映射 $L\times R^{\prime}\to H$ 是满射。

(3) 一个群同态 $\phi: R\to\mathrm{Aut}(L)$。

在这些解释中，我们最喜欢的是最后一个，因为它没有参考群 $H$——一旦我们构造了一个群同态 $\phi: R\to \mathrm{Aut}(L)$，就可以构造一个短正合序列 $L\to H\to R$。

问题：在 $R$ 和 $L$ 的术语中，$H$ 上的群运算是什么？

命题 任何同态$$\begin{aligned}\phi: R&\to \mathrm{Aut}(L),\\r&\mapsto \phi_{r}.\end{aligned}$$定义了一个群 $H$ 和一个分裂的短正合序列

则(1) 以下定义了集合 $H=L\times R$ 上的群结构：

$$\begin{aligned} H\times H&\to H\\ (l_{1},r_{1})\cdot(l_{2},r_{2})&:=(l_{1}\cdot\phi_{r_{1}}(l_{2}),r_{1}r_{2}).\end{aligned}$$

右边等式的右边几乎是 $L\times R$ 的群运算，但在我们将 $l_{1}$ 与 $l_{2}$ 相乘之前，我们将 $l_{2}$“扭曲”为 $L$ 的另一个元素——即 $r_{1}$ 在同态 $\phi:R\to \mathrm{Aut}(L)$ 下的值 $\phi_{r_{1}}(l_{2})$。此外，

(2) 集合 ${(l,1)}$ 是一个正规子群，同构于 $L$，

(3) 集合 ${(1,r)}$ 是一个子群，同构于 $R$。

证明：结合律：$$\begin{aligned}(l_{1},r_{1})\cdot((l_{2},r_{2})\cdot(l_{3},r_{3}))&=(l_{1},r_{1})\cdot(l_{2}\cdot\phi_{r_{2}}(l_{3}),r_{2}r_{3})\\&=(l_{1}\cdot\phi_{r_{1}}(l_{2}\cdot\phi_{r_{2}}(l_{3})),r_{1}(r_{2}r_{3}))\\&=(l_{1}\cdot\phi_{r_{1}}(l_{2})\cdot\phi_{r_{1}}(\phi_{r_{2}}(l_{3})),r_{1}(r_{2}r_{3}))\\&=(l_{1}\cdot\phi_{r_{1}}(l_{2})\cdot\phi_{r_{1}r_{2}}(l_{3}),(r_{1}r_{2})r_{3})\\&=(l_{1}\cdot\phi_{r_{1}}(l_{2}),r_{1}r_{2})\cdot(l_{3},r_{3})\\&=((l_{1},r_{1})\cdot(l_{2},r_{2}))\cdot(l_{3},r_{3})\end{aligned}$$第三个等式是因为 $\phi_{r_{1}}$ 是同态。第四个等式是因为 $\phi:R\to \mathrm{Aut}(L)$ 是同态。

单位元：

$$\begin{aligned}(1_{L},1_{R})\cdot (l,r)&=(1_{L}\cdot \phi_{1_{R}}(l), 1_{R}\cdot r)\\&=(1_{L}\cdot l, 1_{R}\cdot r)\\&=(l,r)\end{aligned}$$第二个等式是因为 $\phi$ 是同态，所以 $\phi_{1}=1$。

逆元：

命题 $(l,r)^{-1}=(\phi_{r^{-1}}(l^{-1}),r^{-1})$。

证明：$$\begin{aligned}(l,r)\cdot(\phi_{r^{-1}}(l^{-1}),r^{-1})&=(l\cdot\phi_{r}(\phi_{r^{-1}}(l^{-1})),rr^{-1})\&=(l\cdot\phi_{rr^{-1}}(l^{-1}),rr^{-1})\\&=(l\cdot l^{-1},rr^{-1})\\&=(1_{L},1_{R})\end{aligned}$$

第二个等式是因为 $\phi:R\to \mathrm{Aut}(L)$ 是同态，所以 $\phi_{r}\circ\phi_{r^{\prime}}=\phi_{rr^{\prime}}$。第三个等式是因为 $\phi$ 是群同态，所以 $\phi_{1}=\mathrm{id}_{L}$。

$$\begin{aligned}(\phi_{r^{-1}}(l^{-1}),r^{-1})\cdot(l,r)&=(\phi_{r^{-1}}(l^{-1})\cdot\phi_{r^{-1}}(l),r^{-1}r)\\&=(\phi_{r^{-1}}(l^{-1}l),r^{-1}r)\\&=(\phi_{r^{-1}}(1_{L}),1_{R})\\&=(1_{L},1_{R})\end{aligned}$$

第二个等式是因为 $\phi_{r^{-1}}: L\to L$ 是群同态。最后一个等式是因为 $\phi_{r^{-1}}$ 是群同态，所以 $\phi_{r^{-1}}=1$。

$$~\tag*{$\square$}$$

因此，它确实定义了一个群。

$$~\tag*{$\square$}$$

定义 我们用符号$$L\rtimes_{\phi} R$$表示这个群。当 $\phi$ 是隐含的时，我们写作$$L\rtimes R，$$并称 $L\rtimes R$ 是 $L$ 和 $R$ 的半直积（semi-direct product）。

注 我们使用“一个”是因为不同的 $\phi$ 可能会产生不同的群。虽然“和”通常是对顺序无动于衷的连词，但 $L$ 和 $R$ 在这里扮演着截然不同的角色！

注 为什么用 $\rtimes$？通常，当 $N$ 是 $G$ 的正规子群时，我们写作 $N\triangleleft G$。$\rtimes$ 是 $\triangleleft$（正规子群）和 $\times$（乘积）的混血产物。任何

都引出一个映射$$R\to\mathrm{Aut}(L)。$$如何引出？通过共轭，因为$$\begin{aligned}L\subset H&~\text{是正规子群},\\C_{h}: L&\to L\\l&\mapsto hlh^{-1}\end{aligned}$$是 $L$ 上的一个群自同构。

通过基本与作业相同的论证，我们得到了一个同态$$\begin{aligned}H&\to\mathrm{Aut}(L)\\h&\mapsto C_{h}\end{aligned}$$复合映射

就是同态 $\phi$。

问题：$R$ 在 $L\subset L\rtimes R$ 上如何作用？

命题 $(1_{L},r)\cdot(l,1_{R})\cdot(1_{L},r^{-1})=(\phi_{r}(l),1_{R})$。换句话说，在 $L\rtimes R$ 中，由 $r$ 的共轭恢复 $\phi_{r}$。

证明：$$\begin{aligned}(1_{L},r)\cdot(l,1_{R})\cdot(1_{L},r^{-1})&=(1_{L}\cdot\phi_{r}(l),r\cdot 1_{R})\cdot (1_{L},r^{-1})\&=(\phi_{r}(l)\cdot \phi(1_{L}), rr^{-1})\&=(\phi_{r}(l\cdot 1_{L}),1_{R})\&=(\phi_{r}(l),1_{R})\end{aligned}$$$$~\tag*{$\square$}$$

我们现在有足够的要素来证明定理 (*)。

核心思想是：

• 如果 $L\subset H$ 是正规子群，那么 $H\curvearrowright L$ 通过共轭作用。

• 给定一个分裂

  
  

那么 $R$ 也有共轭作用$$R\xrightarrow{\phi}\mathrm{Aut}(L)。$$

• $L\rtimes R$ 是一个群，其中 $R$ 在 $L$ 上的共轭作用与 $\phi$ 一致。

现在让我们证明 $H\cong L\rtimes R$！

要看到为什么 $L\rtimes R\cong H$，我们需要一个引理。

引理 对于所有 $h\in H$，存在且唯一的 $l\in L$ 和 $r\in R$，使得 $h=l\cdot j(r)$。

证明：我们知道图

是交换的。（即 $z\circ q=\psi$。）

给定一个分裂 $H\xleftarrow{j} R$，我们看到$$z\circ q\circ j=\psi\circ j=\mathrm{id}_{R}$$由于 $z$ 是一个同构，它有一个逆映射 $z^{-1}$：$$q\circ j=z^{-1}.$$$z^{-1}$ 也是一个群同构。

$z^{-1}$ 是一个双射意味着对于所有 $h\in H$，存在且唯一的 $r$，使得 $q\circ j(r)=[h]\in H/L$。

$\Rightarrow$ 存在且唯一的 $r\in R$，使得 $j(r)\in Lh=[h]$。

$\Rightarrow$ 存在且唯一的 $r\in R$，使得 $[j(r)]=[h]$。

$\Rightarrow$ 存在且唯一的 $r\in R$，使得 $h=l\cdot j(r)$，对于某个 $l\in L$。

当然，给定 $h$ 和 $j(r)$，$l$ 是唯一确定的：$$l=h\cdot j(r)^{-1}$$

因此确实，对于所有 $h\in H$，存在且唯一的 $l,r$，使得 $h=l\cdot j(r)$。$$~\tag*{$\square$}$$

现在我们可以证明：

定理 设 为一个分裂的短正合序列，$\phi: R\to \mathrm{Aut}(L)$ 为引发的作用。则$$H\cong L\rtimes_{\phi} R.$$

证明：考虑映射$$\begin{aligned}L\rtimes_{\phi} R&\xrightarrow{\alpha}H\\(l,r)&\mapsto l\cdot j(r)\end{aligned}$$则$$(l_{1}\cdot\phi_{r_{1}}(l_{2}),r_{1}r_{2})\mapsto l_{1}\phi_{r_{1}}(l_{2})j(r_{1})j(r_{2})。$$但根据定义，$$\phi_{r_{1}}(l_{2})=j(r_{1})l_{2}j(r_{1})^{-1}。$$因此$$\begin{aligned}\alpha((l_{1},r_{1})\cdot (l_{2},r_{2}))&=\alpha((l_{1}\phi_{r_{1}}(l_{2}),r_{1}r_{2}))\\&=l_{1}\phi_{r_{1}}(l_{2})j(r_{1})j(r_{2})\\&=l_{1}j(r_{1})l_{2}j(r_{1})^{-1}j(r_{1})j(r_{2})\\&=l_{1}j(r_{1})l_{2}j(r_{2})\\&=\alpha((l_{1},r_{1}))\cdot\alpha((l_{1},r_{2}))\end{aligned}$$所以 $\alpha$ 是一个同态。

根据引理 11.8，对于所有 $h\in H$，存在且唯一的 $l\in L$ 和 $r\in R$，使得$$h=l\cdot j(r)。$$因此 $\alpha$ 是一个双射。$$~\tag*{$\square$}$$

这足以表明分裂的短正合序列与半直积是同样的数据量：

• 给定
  

我们通过共轭得到 $\phi: R\to\mathrm{Aut}(L)$。

• 根据定理，$H\xleftarrow{\alpha}L\rtimes R$ 是一个同构。

• 所以我们有一个满射 $L\rtimes R\xrightarrow{\alpha}H\xrightarrow{\psi}R$。

• 由于 $\alpha$ 是同构，因此$$\begin{aligned}\ker(\psi\circ\alpha)&=\alpha^{-1}(\ker\psi)\&=\alpha^{-1}(L)\&={(l,1_{R})}\subset L\rtimes R\end{aligned}$$根据引理 11.8。

• 因此我们有一个短完全序列$$\begin{aligned}L&\to L\rtimes R\xrightarrow{\psi\circ\alpha}R\\l&\mapsto(l,1_{R})\end{aligned}$$具有分裂

情况可以总结为以下图是交换的：

（即你可以绘制的任何子方块都是交换的。）

例 回忆 $SO_{n}(\mathbb{R})\subset O_{n}(\mathbb{R})$ 是一个指数为 $2$ 的子群。根据定义，$SO_{n}(\mathbb{R})=\ker(O_{n}(\mathbb{R})\xrightarrow{\det}\mathbb{R}^{\times})$，任何核都是一个正规子群。所以它是正规的。（或者你可以使用任何指数为二的子群都是正规的事实。）因此我们有一个短正合序列

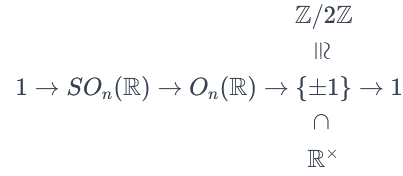
这个序列允许很多不同的分裂。为了具体化，取 $n=2$。

例如，$$O_{2}(\mathbb{R})\leftarrow\mathbb{Z}/2\mathbb{Z}:j$$