共14条回复
时间正序
- 时间正序
- 时间倒序
- 评论最多
1条评论 评论
- 1
once
11月前
2025-3-10 13:57:49
给三角形一个顶点建系,剩下两点用坐标表示然后用勾股表示中线长度做等量关系,得到方程最后解出来顶点横坐标是三角形底的1/2
建议放题目互答,水帖太多了不好找
2条评论 评论
3条评论 评论
载酒裁决(逐日时刻)
11月前
2025-3-10 15:01:57
感觉写的太简陋了
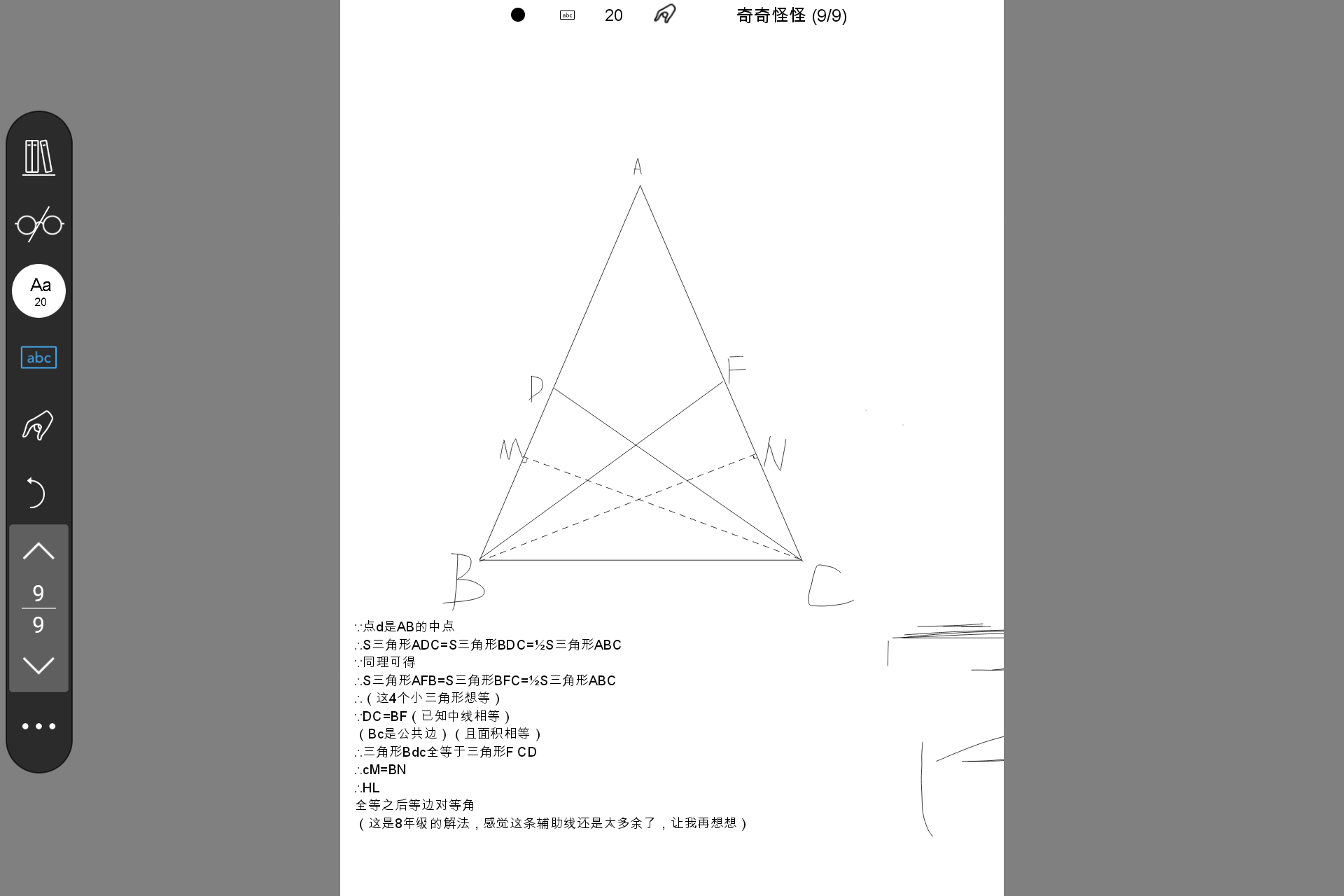
我不确定两条边和面积相等,能不能证明全等
感觉这个思路感觉像是8年级的
可能是课内的题解多了导致的
没有用到一点点高中的内容也是真的美醉了。
2条评论 评论
2条评论 评论
我比带土更爱琳
9月前
2025-5-11 15:37:21
想到了一个有意思的命题:若一个三角形两个角的平分线相等,则这个三角形是等腰三角形。自己试了,很难,谁能证明一下。
3条评论 评论

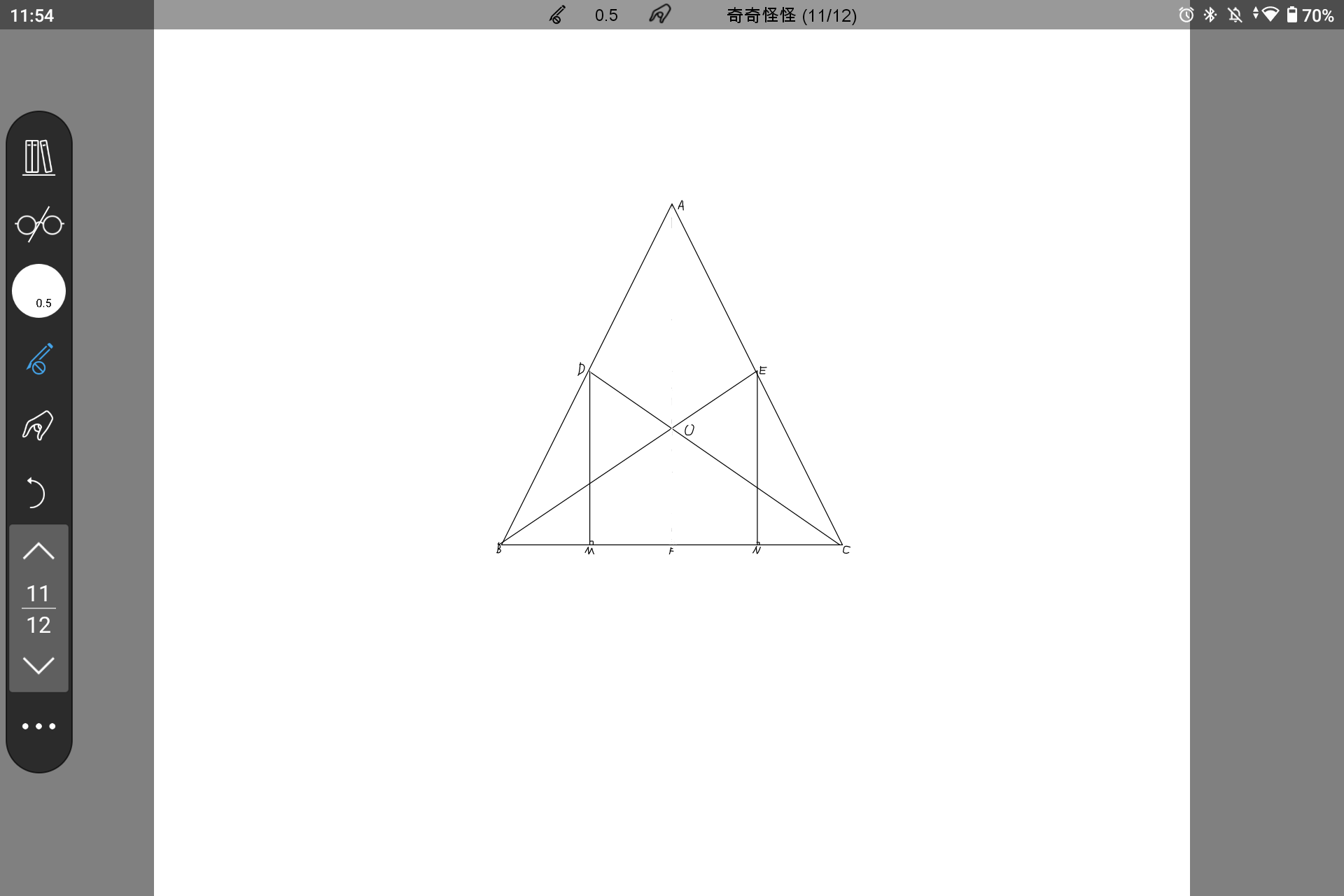
 余弦定理直接秒了
余弦定理直接秒了