物理

圆锥曲线（基础）

本帖由[论坛资料室]赞助播出

评论区有例题！！！

5.3已更抛物线

后面还有直线与圆锥曲线、极坐标中的圆锥曲线

注：只是基础！！！（本人不搞数竞）应该可以用在物理题内

～～～～～～～～～～～～～～～～～～～分界线～～～～～～～～～～～～～～～～～～

椭圆、双曲线、抛物线为三个最常见的圆锥曲线

首先为什么它们叫圆锥曲线呢？

在一个圆锥内任意取一截面得一截线

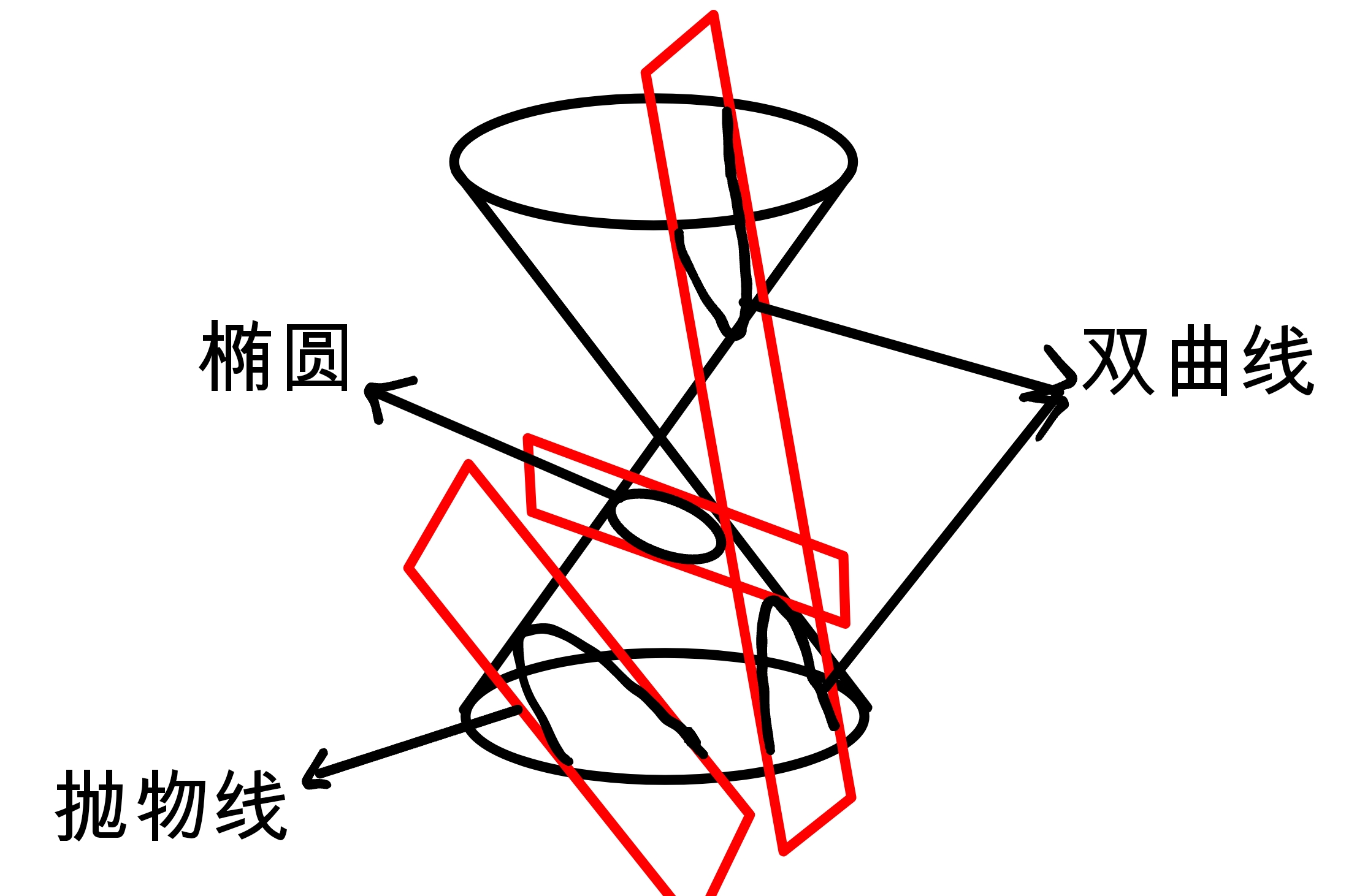
我们惊奇地发现，三种截线正好为 椭圆、双曲线、抛物线

于是赐名：圆锥曲线

$\Huge{Ⅰ.椭圆}$

$\large{1.椭圆的定义}$ 

第一定义：平面内与两定点F1,F2的距离之和等于常数2a>|F1F2|的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点，两焦点的距离2c叫做椭圆的焦距。

第二定义：动点M到定点F的距离和它到定直线l（F不在l上）的距离之比等于常数e（0<e<1）（后文将提及的偏心率e=$\frac{a}{c}$），则动点M的轨迹叫做椭圆。

$\large{2.椭圆的标准方程}$

1.$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0) 

中心在原点，焦点在x轴上

图形：

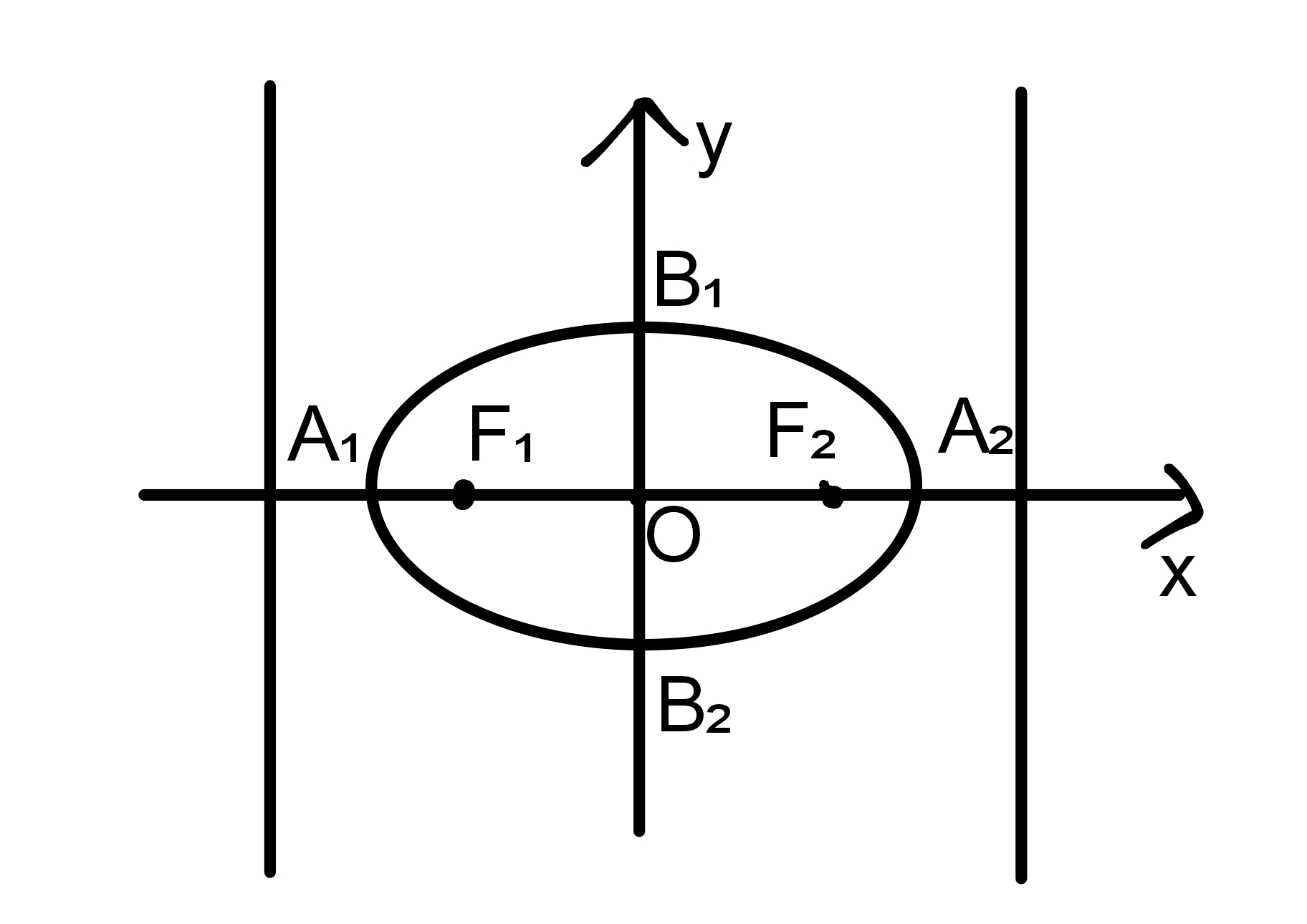
范围：ⅠxⅠ≤a，|y|≤b

顶点：A₁(-a,0),A₂(a,0),B₁(0,-b),B₂(0,b)

对称轴：x轴，y轴，长轴长2a，短轴长2b，焦点在长轴上

焦点：F₁(-c,0),F₂(c,0)$(c^2=a^2-b^2)$

焦距:|F₁F₂|=2c(c>0)

离心率：e=$\frac{c}{a}$(0<e<1)

$准线：x=±\frac{a^2}{c}$

2.$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$(a>b>0)

中心在原点，焦点在y轴上

图形：

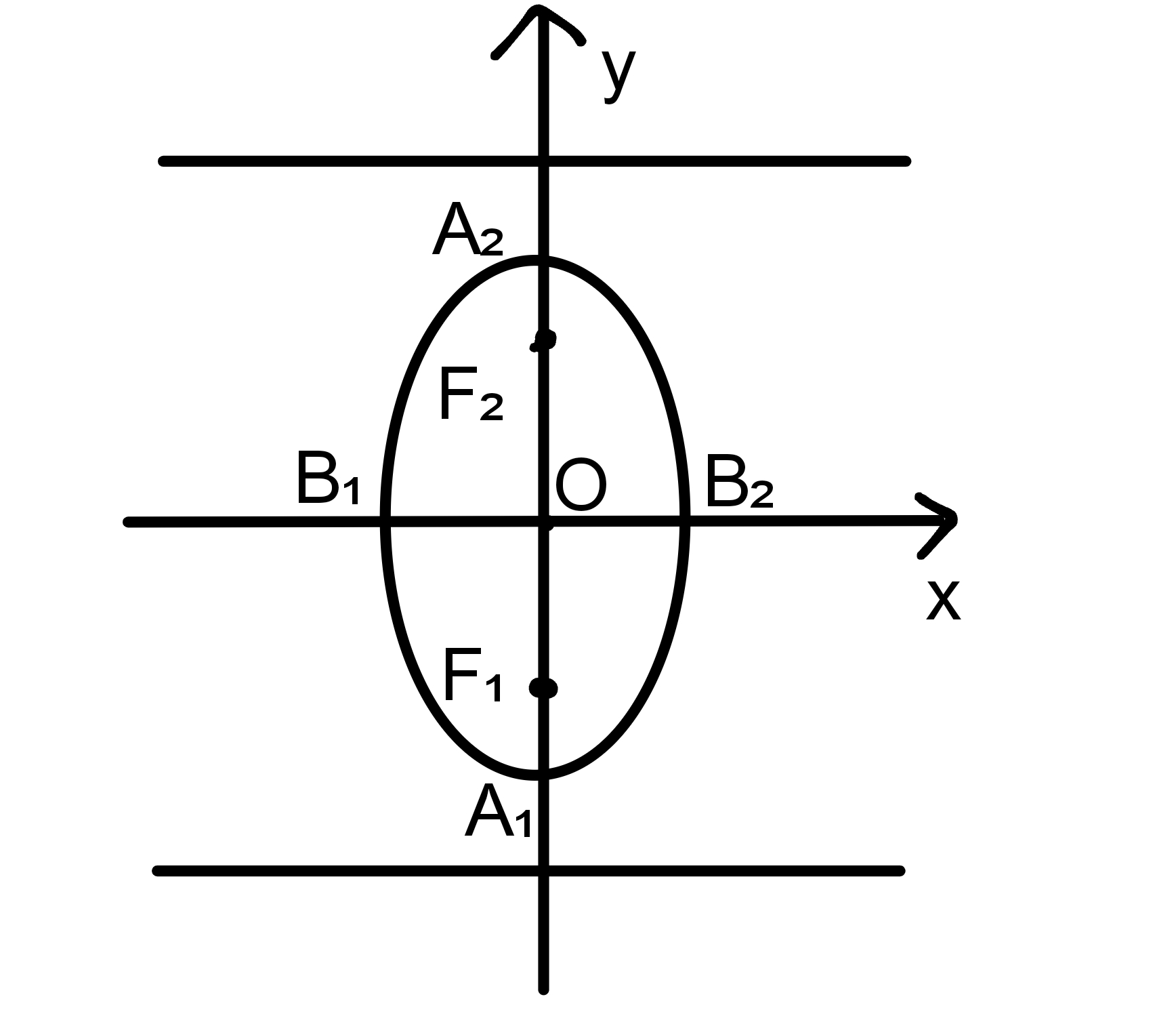
范围：ⅠxⅠ≤b，|y|≤a

顶点：A₁(0,-a),A₂(0,a),B₁(-b,0),B₂(b,0)

对称轴：x轴，y轴，长轴长2a，短轴长2b，焦点在长轴上

焦点：F₁(0,-c),F₂(0,c)$(c^2=a^2-b^2)$

焦距:|F₁F₂|=2c(c>0)

离心率：e=$\frac{c}{a}$(0<e<1)

$准线：y=±\frac{a^2}{c}$

$\large{3.焦点弦}$

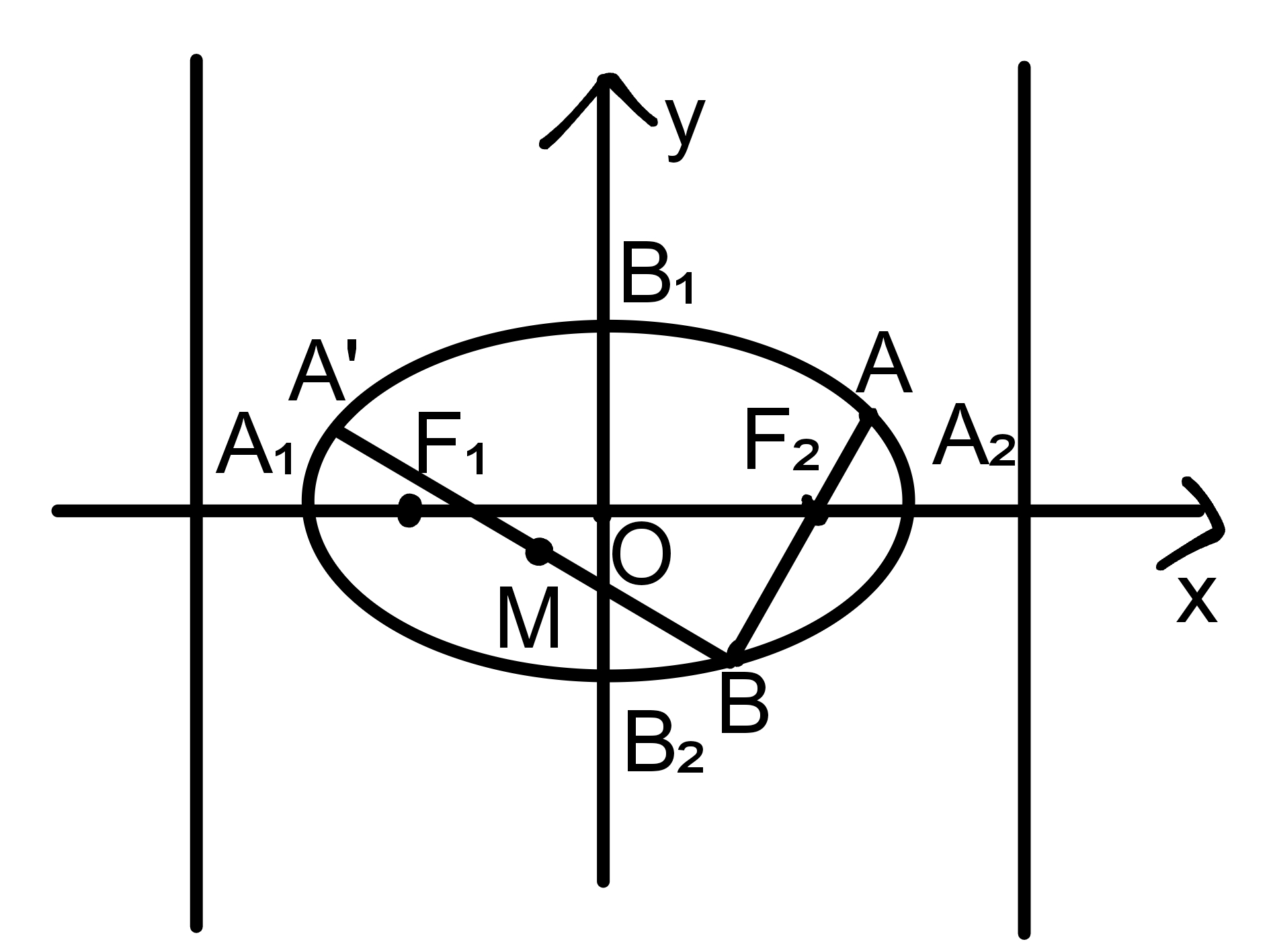
AB为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的焦点弦，A(x₁,y₁),B(x₂,y₂),弦中点$M(x_0，y_0)$

$(1)弦长：l=2a±2ex_0$

$(2)焦点弦中通径最短，长轴最长：{{l_m}_i}_n=\frac{2b^2}{a},{{l_m}_a}_x=2a$

$(3)焦半径：r_1=a+ex_0,r_2=a-ex_0$

$\large{4.中点弦}$

A'B为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的弦,A'(x₁,y₁),B(x₂,y₂),弦中点$M(x_0，y_0)$

$(1)斜率：k=-\frac{b^2x_0}{a^2y_0}$

$(2)弦A'B的斜率与弦中点M和椭圆中心O的连线的斜率之积为定值-\frac{b^2}{a^2}$

$\Huge{Ⅱ.双曲线}$

$\large{1.双曲线的定义}$ 

第一定义：平面内与两定点F1,F2的距离之差的绝对值等于常数2a<|F1F2|的点的轨迹叫做双曲线。这两个定点叫做双曲线的焦点，两焦点的距离2c叫做双曲线的焦距。

第二定义：动点M到定点F的距离和它到定直线l（F不在l上）的距离之比等于常数e（e>1），则动点M的轨迹叫做双曲线，定点F为焦点，定直线l称为准线，常数e称为离心率。

$\large{2.双曲线的标准方程}$

1.$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0) 

中心在原点，焦点在x轴上

图形：

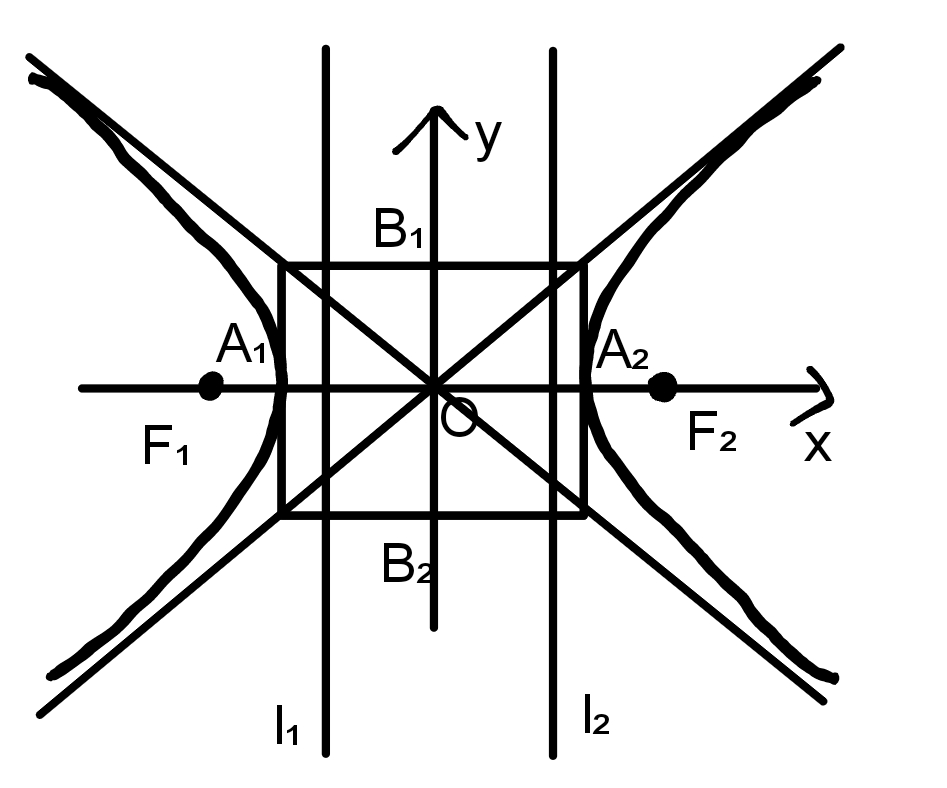
范围：ⅠxⅠ≥a

顶点：A₁(-a,0),A₂(a,0)

对称性：x轴，y轴，原点

轴：实轴长|A₁A₂|=2a，虚轴长|B₁B₂|=2b，焦点在长轴上

离心率：$e=\frac{c}{a}$(e>1)

焦点：F₁(-c,0),F₂(c,0)$(c^2=a^2+b^2)$

焦距:|F₁F₂|=2c(c>0)

$准线：x=±\frac{a^2}{c}$

$焦准距：p=\frac{b^2}{c}$

$渐进线：y=±\frac{b}{a}x$

$通径：通径长\frac{2b^2}{a}$

焦半径公式：P(x₁,y₁)在左支和右支的情况分别为：

左支：|PF₁|=-a-ex₁，|PF₂|=a-ex₁

右支：|PF₁|=a+ex₁，|PF₂|=-a+ex₁

2.$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$(a>0,b>0) 

中心在原点，焦点在y轴上

图形：

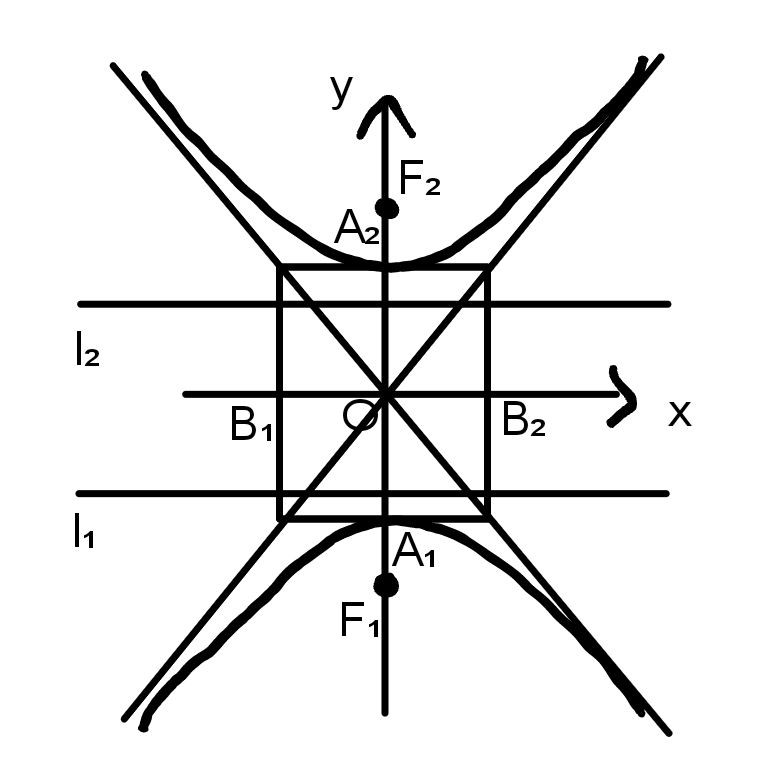
范围：ⅠyⅠ≥a

顶点：A₁(0,-a),A₂(0,a)

对称性：x轴，y轴，原点

轴：实轴长|A₁A₂|=2a，虚轴长|B₁B₂|=2b，焦点在长轴上

离心率：$e=\frac{c}{a}$(e>1)

焦点：F₁(0,-c),F₂(0,c)$(c^2=a^2+b^2)$

焦距:|F₁F₂|=2c(c>0)

$准线：y=±\frac{a^2}{c}$

$焦准距：p=\frac{b^2}{c}$

$渐进线：y=±\frac{a}{b}x$

$通径：通径长\frac{2b^2}{a}$

焦半径公式：P(x₁,y₁)在下支和上支的情况分别为：

下支：|PF₁|=-a-ey₁，|PF₂|=a-ey₁

上支：|PF₁|=a+ey₁，|PF₂|=-a+ey₁

$\large{3.焦点弦}$

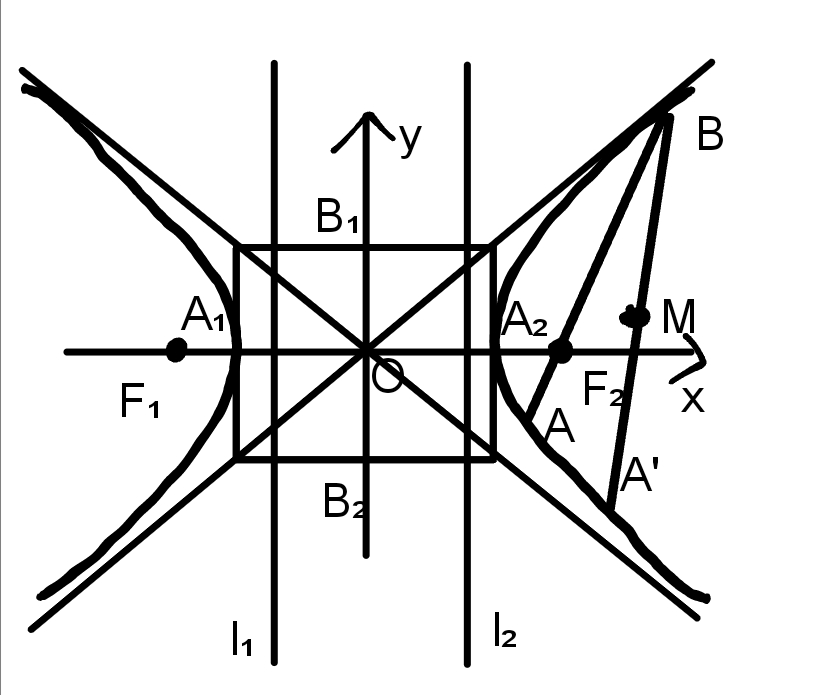
AB为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的焦点弦，A(x₁,y₁),B(x₂,y₂),弦中点$M(x_0，y_0)$

$(1)弦长：l=-2a±2ex_0$

$(2)焦点弦中通径最短，长轴最长：{{l_m}_i}_n=\frac{2b^2}{a},{{l_m}_a}_x=∞$

(3)焦半径公式：P(x₁,y₁)在左支和右支的情况分别为：

左支：r₁=-a-ex₁，r₂=a-ex₁

右支：r₁=a+ex₁，r₂=-a+ex₁

$\large{4.中点弦}$

A'B为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的弦,A'(x₁,y₁),B(x₂,y₂),弦中点$M(x_0，y_0)$

$(1)斜率：k=\frac{b^2x_0}{a^2y_0}$

$(2)弦AB的斜率与弦中点M和双曲线中心O的连线的斜率之积为定值\frac{b^2}{a^2}$

$\Huge{Ⅲ.抛物线}$

$\large{1.抛物线的定义}$

物理定义：不考虑空气摩擦，只考虑重力的情况下，将物体斜着抛出去，物体在空中划过的轨迹被称作抛物线。

数学定义：平面内与一个定点F和一条定直线l的距离相等（都为$\frac{p}{2}$）的点的轨迹叫做抛物线，点F叫做抛物线的焦点，直线l叫做抛物线的准线，定点F不在定直线l上。它与椭圆、双曲线的第二定义相仿，仅比值（离心率e）不同，当e=1时为抛物线，当0<e<1时为椭圆，当e>1时为双曲线。

$\large{2抛物线的标准方程}$

1.$y^2=2px$(p>0) 

顶点在原点，焦点在x轴上

图形：

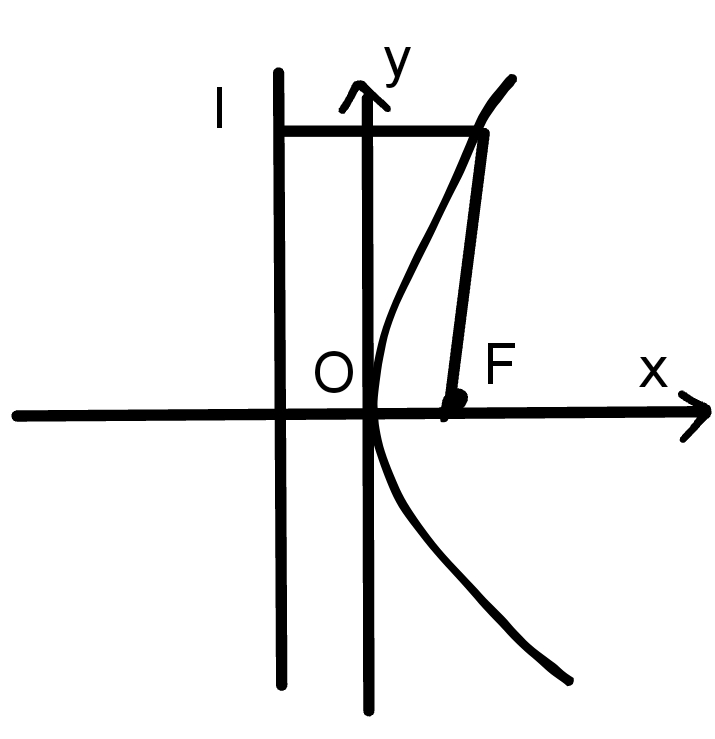
范围：x≥0，y∈R

顶点：原点O（0,0）

对称性：x轴

$焦点：F(\frac{p}{2},0)$

$准线：x=-\frac{p}{2}$

离心率：e=1

$焦半径公式：P(x_0,y_0)$为抛物线上任意一点

$|PF|=x_0+\frac{p}{2}$

2.$y^2=-2px$(p>0) 

顶点在原点，焦点在x轴上

图形：

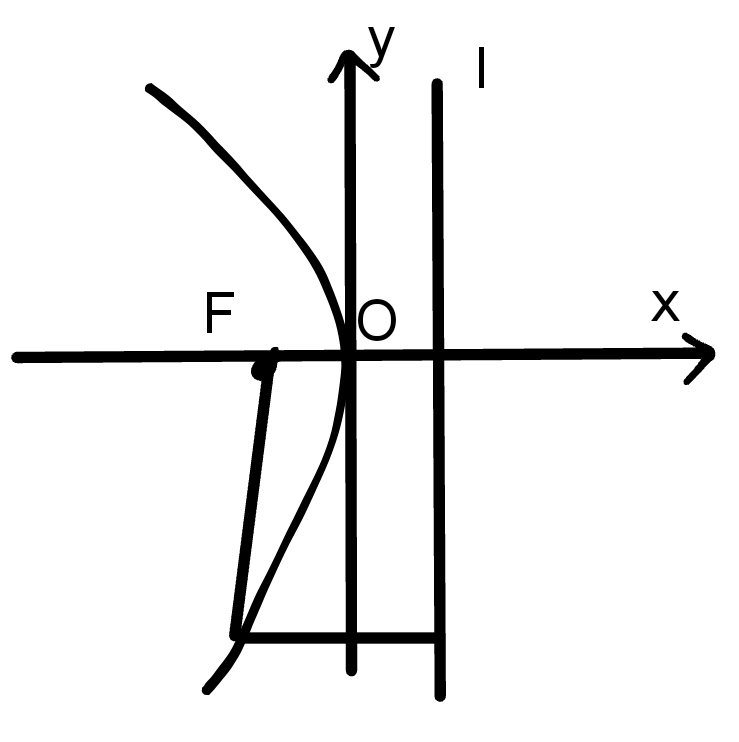
范围：x≤0，y∈R

顶点：原点O（0,0）

对称性：x轴

$焦点：F(\frac{-p}{2},0)$

$准线：x=\frac{p}{2}$

离心率：e=1

$焦半径公式：P(x_0,y_0)$为抛物线上任意一点

$|PF|=-x_0+\frac{p}{2}$

3.$x^2=2py$(p>0) 

顶点在原点，焦点在y轴上

图形：

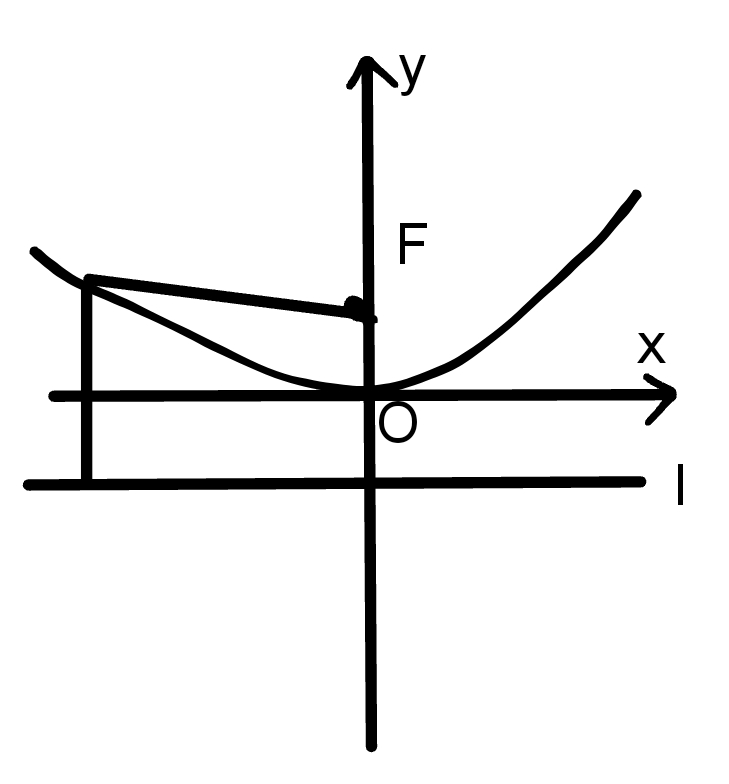
范围：y≥0，x∈R

顶点：原点O（0,0）

对称性：x轴

$焦点：F(0,\frac{p}{2})$

$准线：y=-\frac{p}{2}$

离心率：e=1

$焦半径公式：P(x_0,y_0)$为抛物线上任意一点

$|PF|=y_0+\frac{p}{2}$

4.$y^2=2px$(p>0) 

顶点在原点，焦点在y轴上

图形：

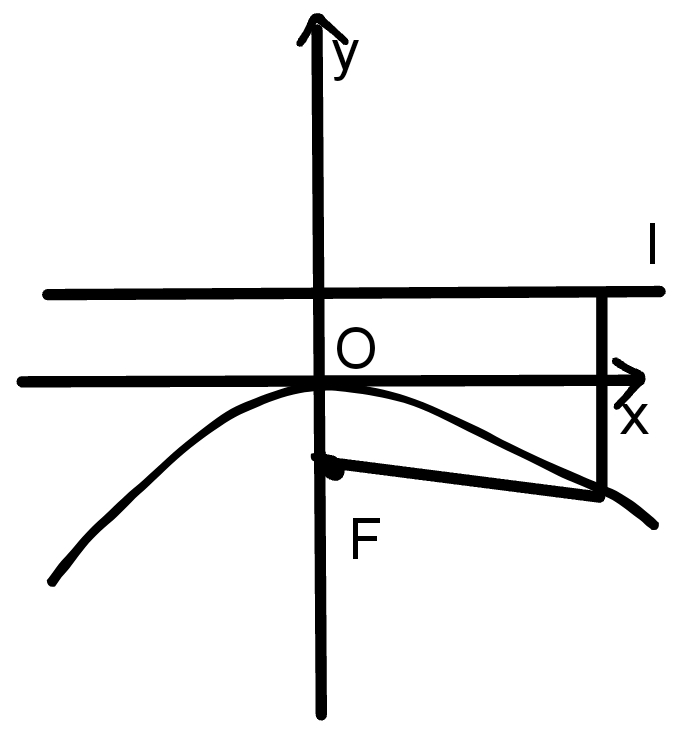
范围：y≤0，x∈R

顶点：原点O（0,0）

对称性：y轴

$焦点：F(0,-\frac{p}{2})$

$准线：y=\frac{p}{2}$

离心率：e=1

$焦半径公式：P(x_0,y_0)$为抛物线上任意一点

$|PF|=-y_0+\frac{p}{2}$

抛物线常用方法：对于抛物线$y^2=2px$(p≠0) 上的点的坐标设为$（\frac{y^2}{2p},0）$，以简化运算。

$\Huge{Ⅳ.直线与圆锥曲线的位置关系}$

$\large{1.直线与圆锥曲线的位置关系}$

$\large{2.圆锥曲线的切线方程}$

椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0) 在点$P（x_0,y_0）$处的切线方程是$\frac{xx_0}{a^2}+\frac{yy_0}{b^2}=1$。

双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0) 在点$P（x_0,y_0）$处的切线方程是$\frac{xx_0}{a^2}-\frac{yy_0}{b^2}=1$。

抛物线$y^2=2px$(p>0)在点$P（x_0,y_0）$处的切线方程是$y_0y=p(x+x_0)$。

一般二次曲线$Ax^2+Bxy+Cy^2+Dx+Ey+F=0$(A、B、C不同时为0）过它上面一点$P（x_0,y_0）$的切线方程为：$Ax_0x+Cy_0y+B\frac{x_0y+y_0x}{2}+D\frac{x+x_0}{2}+E\frac{y+y_0}{2}F=0$。

还没结束。。。。。。