数学

[代数专题]平面直角坐标系常用计算公式

[2025年7月9日已更新]

$1.两点(Point)间距离公式$

$平面直角坐标系：设A(x_1，y_1)，B(x_2，y_2)为平面直角坐标系两点，则A和B两点之间的距离$

$d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$

$空间直角坐标系：设A(x_1，y_1，z_1)，B(x_2，y_2，z_2)，则AB两点之间的距离$

$d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$

$2.中点(Midpoint)坐标公式$

$平面直角坐标系：设A(x_1，y_1)，B(x_2，y_2)，则线段AB中点的坐标为$

$(\dfrac{x_1+x_2}{2}，\dfrac{y_1+y_2}{2})$

$空间直角坐标系：设A(x_1，y_1，z_1)，B(x_2，y_2，z_2)，则线段AB中点的坐标为$

$(\dfrac{x_1+x_2}{2}，\dfrac{y_1+y_2}{2}，\dfrac{z_1+z_2}{2})$

$3.点到直线(Straight Line)距离公式$

$①一般式：点P(x_0，y_0)到直线Ax+By+C=0(A，B不同时为0)的距离$

$d=\dfrac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}$

$②斜截式：点P(x_0，y_0)到直线y=kx+b的距离$

$d=\dfrac{|kx_0-y_0+b|}{\sqrt{k^2+1}}$

$4.直线斜率(Slope)公式$

$过两点A(x_1，y_1)，B(x_2，y_2)[x_1≠x_2]的直线斜率$

$k=\dfrac{y_2-y_1}{x_2-x_1}$

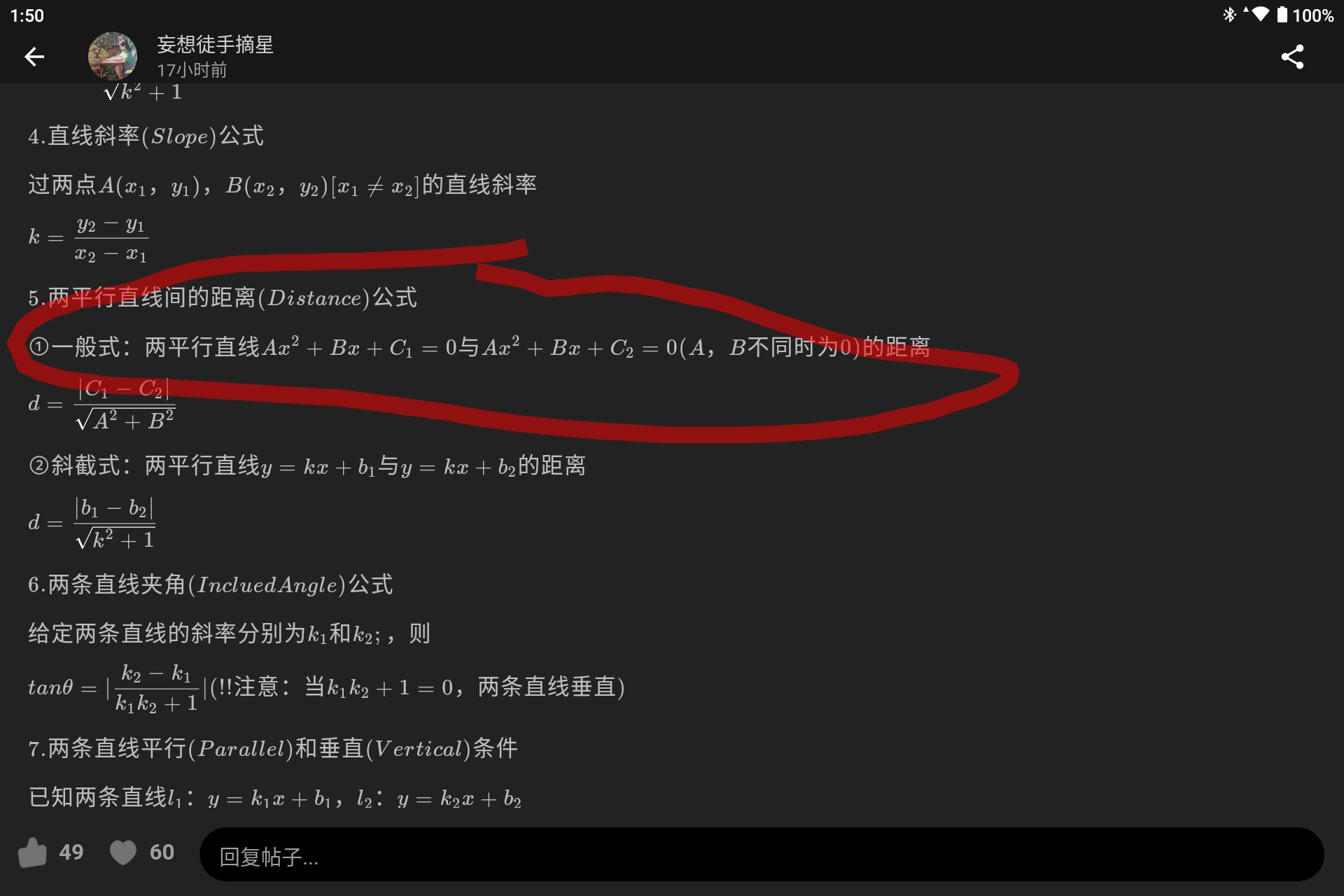
$5.两平行直线间的距离(Distance)公式$

$①一般式：两平行直线Ax+By+C_1=0与Ax+By+C_2=0(A，B不同时为0)的距离$

$d=\dfrac{|C_1-C_2|}{\sqrt{A^2+B^2}}$

$②斜截式：两平行直线y=kx+b_1与y=kx+b_2的距离$

$d=\dfrac{|b_1-b_2|}{\sqrt{k^2+1}}$

$6.两条直线夹角(Inclued Angle)公式$

$给定两条直线的斜率分别为k_{1}和k_{2};，则$

$tanθ=|\dfrac{k_{2}-k_{1}}{k_{1}k_{2}+1}|(!!注意：当k_{1}k_{2}+1=0，两条直线垂直)$

$7.两条直线平行(Parallel)和垂直(Vertical)条件$

$已知两条直线l_1：y=k_1x+b_1，l_2：y=k_2x+b_2$

$①l_1平行于l_2，则k_1=k_2；②l_1垂直于l_2，则k_1k_2=-1$

$8.两条直线交点(Intersection)公式$

$两条直线L_1：y=A_1x+B_1y+C_1=0，L_2：A_2x+B_2y+C_2=0交点(x，y)为：$

$x=\dfrac{B_1C_2-B_2C_1}{A_1B_2-A_2B_1}，$

$y=\dfrac{A_2C_1-A_1C_2}{A_1B_2-A_2B_1}(其中A_1B_2-A_2B_1≠0，即两直线不平行)$

$9.弦长公式$

$抛物线y=ax^2+bx+c(a≠0)与直线y=kx+b分别交于A，B，则AB=\sqrt{k^2+1}×|x_{A}-x_{B}|$

$10.分点公式$

$已知A(x_{1}，y_{1})，B(x_{2}，y_{2})$

$①内分点公式：点P在AB上，且分为m：n，则点P的坐标为$

$(\dfrac{mx_{2}+nx_{1}}{m+n}，\dfrac{my_{2}+ny_{1}}{m+n})$

$②外分点公式：点P在A B延长线上，且分为m：n，则点P的坐标为$

$(\dfrac{mx_{2}-nx_{1}}{m-n}，\dfrac{my_{2}-ny_{1}}{m-n})$

$11.三角形(Triangle)公式$

$设A(x_1，y_1)，B(x_2，y_2)，C(x_3，y_3)$

$⑴三角形面积(Area)公式(鞋带公式)$

$S=\dfrac{|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|}{2}$

$⑵三角形重心(Centroid)坐标公式$

$ΔABC重心G坐标为：(\dfrac{x_1+x_2+x_3}{3}，\dfrac{y_1+y_2+y_3}{3})$

$⑶三角形内心(Incenter)坐标公式$

$设BC=a，AC=b，AB=c，则ΔABC的内心I坐标为：$

$(\dfrac{ax_1+bx_2+cx_3}{a+b+c}，\dfrac{ay_1+by_2+cy_3}{a+b+c})$

$⑷三角形的旁心(Excenter)坐标公式$

$设BC=a，AC=b，AB=c，则ΔABC旁心坐标为：$

$I_A(\dfrac{-ax_1+bx_2+cx_3}{-a+b+c}，\dfrac{-ay_1+by_2+cy_3}{-a+b+c})，$

$I_B(\dfrac{ax_1-bx_2+cx_3}{a-b+c}，\dfrac{ay_1-by_2+cy_3}{a-b+c})，$

$I_C(\dfrac{ax_1+bx_2-cx_3}{a+b-c}，\dfrac{ay_1+by_1-cy_3}{a+b-c}).$(！！看看就行啦)

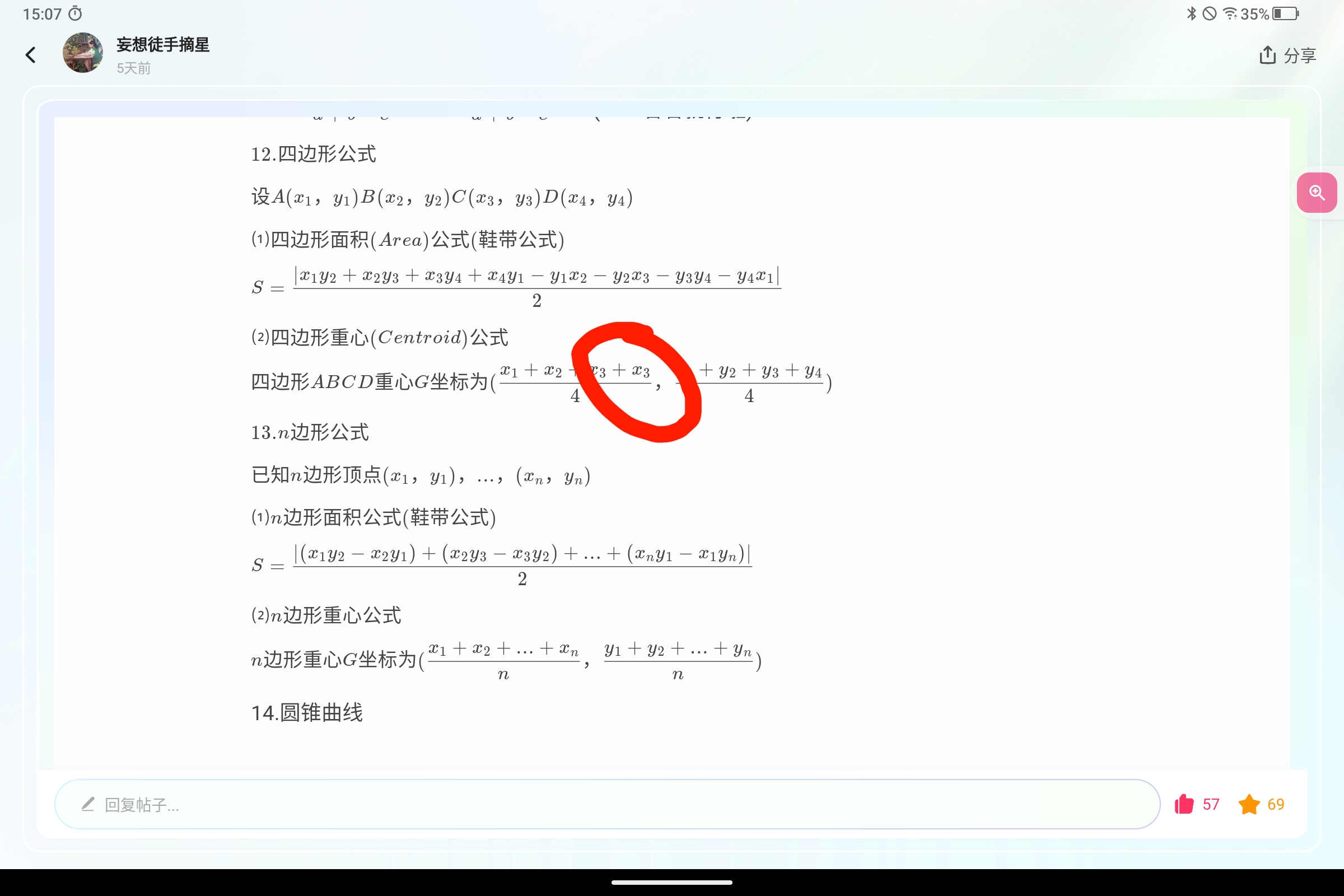
$12.四边形公式$

$设A(x_1，y_1)B(x_2，y_2)C(x_3，y_3)D(x_4，y_4)$

$⑴四边形面积(Area)公式(鞋带公式)$

$S=\dfrac{|x_1y_2+x_2y_3+x_3y_4+x_4y_1-y_1x_2-y_2x_3-y_3y_4-y_4x_1|}{2}$

$⑵四边形重心(Centroid)公式$

$四边形ABCD重心G坐标为(\dfrac{x_1+x_2+x_3+x_3}{4}，\dfrac{y_1+y_2+y_3+y_4}{4})$

$13.n边形公式$

$已知n边形顶点(x_{1}，y_{1})，...，(x_{n}，y_{n})$

$⑴n边形面积公式(鞋带公式)$

$S=\dfrac{|(x_{1}y_{2}-x_{2}y_{1})+(x_{2}y_{3}-x_{3}y_{2})+...+(x_{n}y_{1}-x_{1}y_{n})|}{2}$

$⑵n边形重心公式$

$n边形重心G坐标为(\dfrac{x_{1}+x_{2}+...+x_{n}}{n}，\dfrac{y_{1}+y_{2}+...+y_{n}}{n})$

14.圆锥曲线