数学 抽象代数——基本群
定义 设$X\subset\mathbb{R}^{n}$为一个子集,并固定$x_{0}\in X$。以$x_{0}$为基点的$X$中的一个闭路径(loop)是一个连续函数
$$[0,1]\xrightarrow{\gamma}\mathbb{R}^{n} \tag*{}$$
满足以下条件:
- 对于任意$t\in[0,1]$,有$\gamma(t)\in X$。
- $\gamma(0)=\gamma(1)=x_{0}$。
例 设$X=\mathbb{R}^{n}\setminus\{0\}$,$x_{0}=(1,0)$。
定义 给定两条曲线$\gamma_{1}$和$\gamma_{2}$,如果$\gamma_{1}$可以在不改变$\gamma(0)$和$\gamma(1)$的情况下,通过连续变形变为$\gamma_{2}$,我们称$\gamma_{1}$和$\gamma_{2}$同伦(homotopic)。即,如果存在一个连续映射
$$\begin{aligned} \Gamma: [0,1]\times[a,b]&\to X\\ (t,s)&\mapsto \Gamma(t,s) \end{aligned} \tag*{}$$
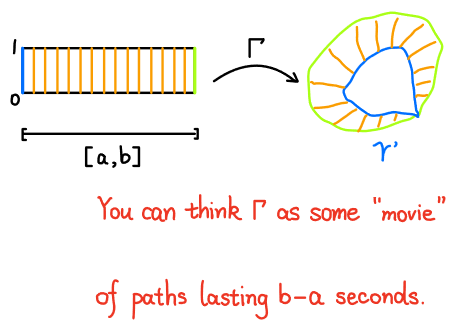
使得
- $\Gamma(t,a)=\gamma_{1}(t)$。
- $\Gamma(t,b)=\gamma_{2}(t)$。
- 对任意$s$,有$\Gamma(0,s)=\Gamma(1,s)=x_{0}$。
其中$[a,b]$是某个区间。
你可以将看作是一段持续$b-a$秒的“路径动画”。
引理 若$\gamma_{1}\sim\gamma_{2}$当且仅当$\gamma_{1}$与$\gamma_{2}$同伦,则$\sim$是一个等价关系。
简单来说:
- 任意路径可以通过“无变形”变回自身。
- 如果$\gamma_{1}$可以变形为$\gamma_{2}$,则$\gamma_{2}$也可以通过反向变形变回$\gamma_{1}$。
- 如果$\gamma_{1}$可以变形为$\gamma_{2}$,而$\gamma_{2}$又可以变形为$\gamma_{3}$,那么可以通过连续执行两次变形来将$\gamma_{1}$变形为$\gamma_{3}$。
定义 定义
$$\pi_{1}(X,x_{0})=\{\text{以}~x_{0}~\text{为基点的闭路径}\}/\sim.\tag*{}$$
称其为以$x_{0}$为基点的$X$的基本群(fundamental group)。
基本群的复合如下:
$$\begin{aligned} \pi_{1}(X,x_{0})\times\pi_{1}(X,x_{0})&\to\pi_{1}(X,x_{0})\\ ([\gamma_{b}],[\gamma_{a}])&\mapsto [\gamma_{b}][\gamma_{a}]. \end{aligned} \tag*{}$$
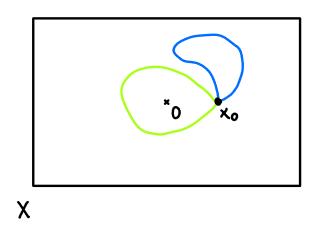
给定两条路径$\gamma_{a}$和$\gamma_{b}$,考虑路径
$$\begin{aligned} \widetilde{\gamma_{b}\circ\gamma_{a}}:[0,2]&\to X\\ t&\mapsto\begin{cases} \gamma_{a}(t)&\text{若}~t\in[0,1]\\ \gamma_{b}(t-1)&\text{若}~t\in[1,2] \end{cases} \end{aligned} \tag*{}$$
将区间$[0,2]$重缩放到$[0,1]$,得到路径
$$\begin{aligned} \gamma_{b}\circ\gamma_{a}:[0,1]&\to X\\ t&\mapsto\begin{cases} \gamma_{a}(2t)&\text{若}~t\in\left[0,\frac{1}{2}\right]\\ \gamma_{b}(2t-1)&\text{若}~t\in\left[\frac{1}{2},1\right] \end{cases} \end{aligned} \tag*{}$$
定义$[\gamma_{b}][\gamma_{a}]=[\gamma_{b}\circ\gamma_{a}]$。
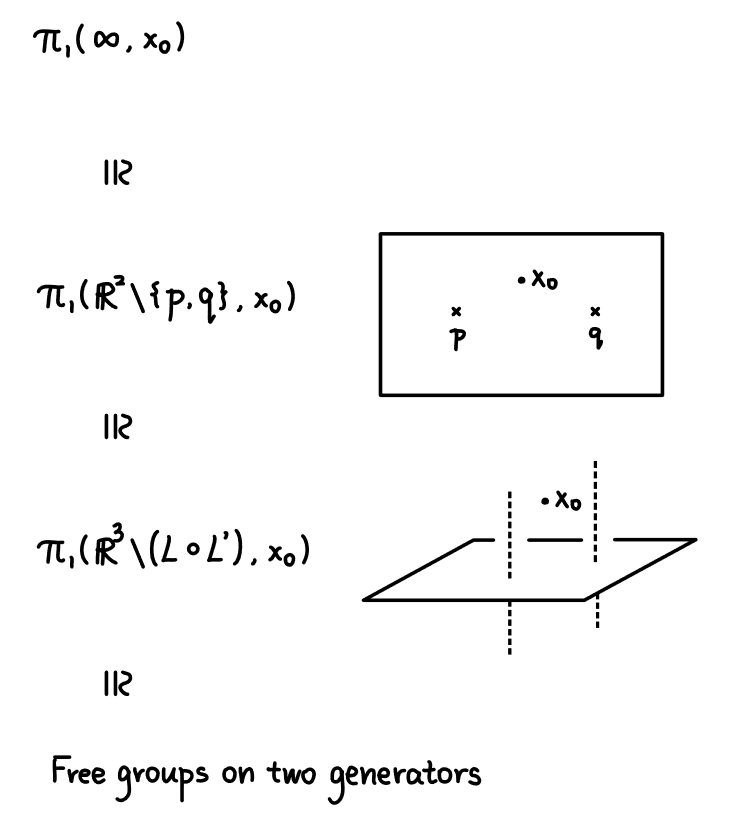
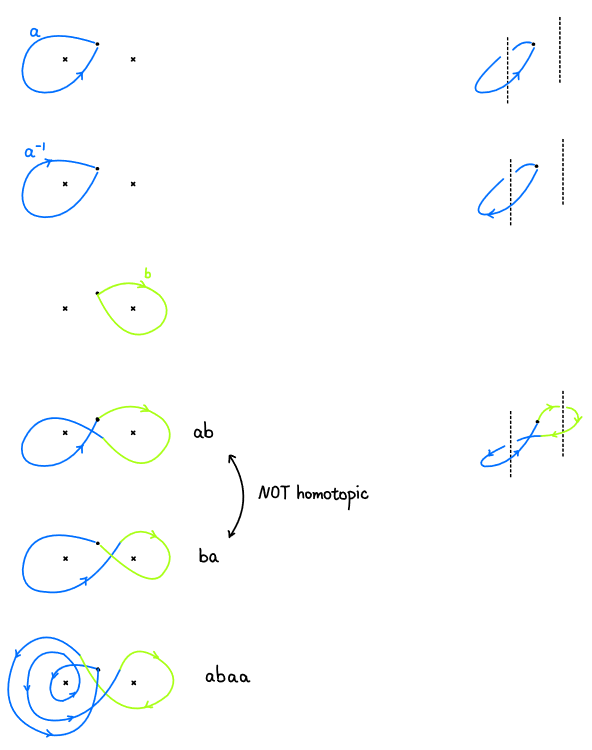
例 考虑$X=\mathbb{R}^{2}\setminus\{p,q\}$, $x_{0}$是任意点。
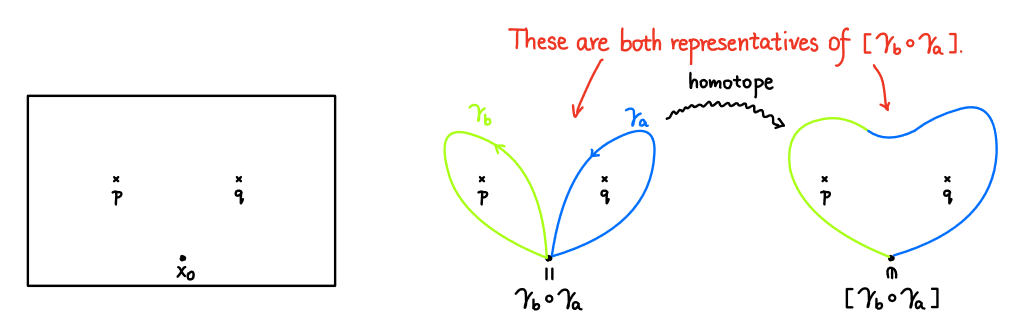
注
- 恒等闭路径$\gamma(t)=x_{0}$对任意$t$恒为单位元。
如果$\gamma$是一条闭路径,而$\gamma_{0}$是恒等路径,那么$\gamma_{0}\circ\gamma$是“快速执行$\gamma$ ,然后静止$\dfrac{1}{2}$秒”的路径。设$\Gamma$为从$\dfrac{1}{2}$秒静止时间逐渐收缩到$0$秒的同伦变换。
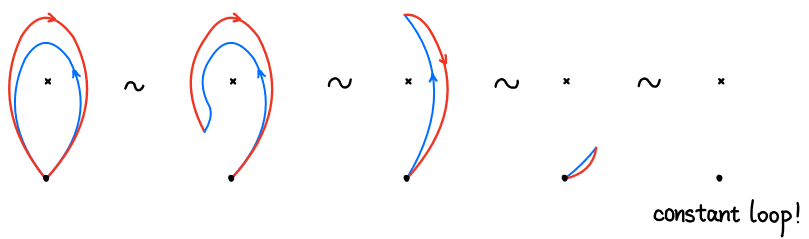
- $\gamma$的逆路径是“反向执行$\gamma$”的闭路径。
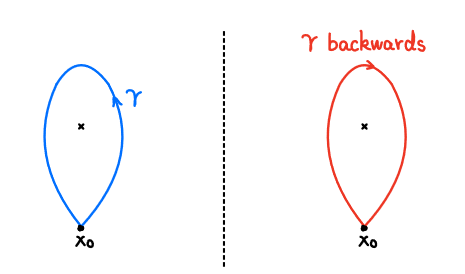
[“$\gamma$反向”$\circ \gamma$]=?
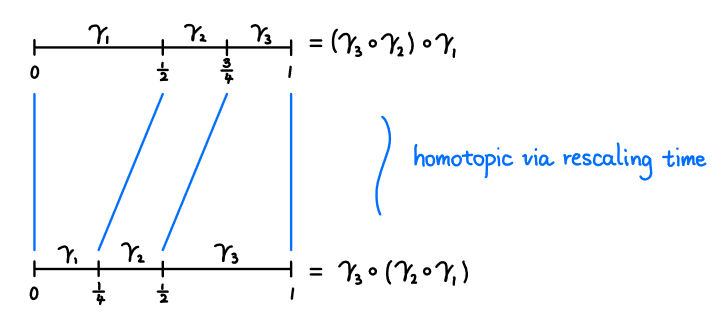
- 最终,路径复合是结合的。
例
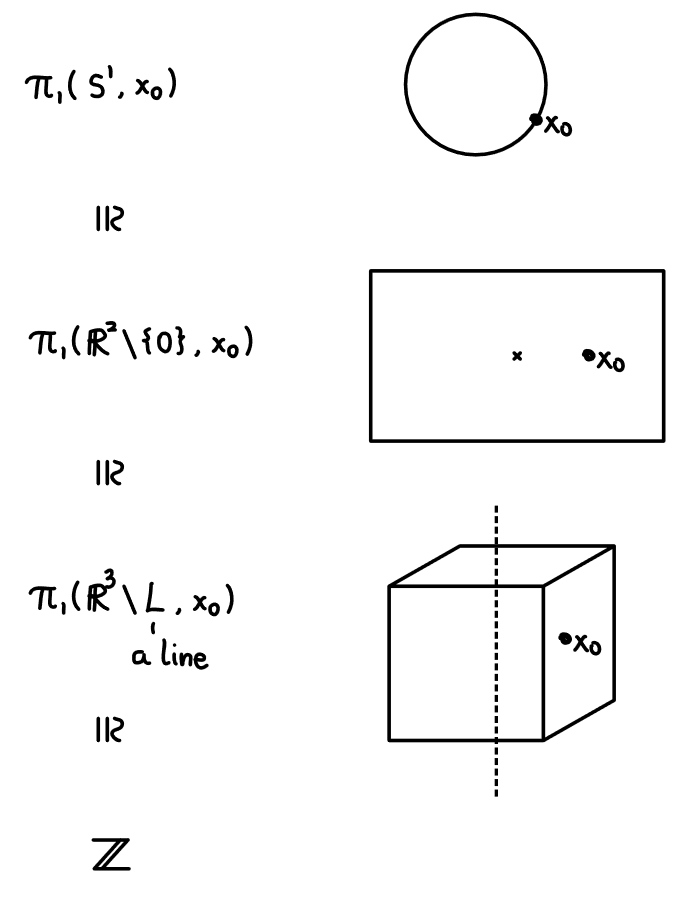
这里不证明同构,但粗略地,可以将路径$\gamma$映射到它的“绕数”。
“路径$\gamma$绕过缺口的次数是多少?”
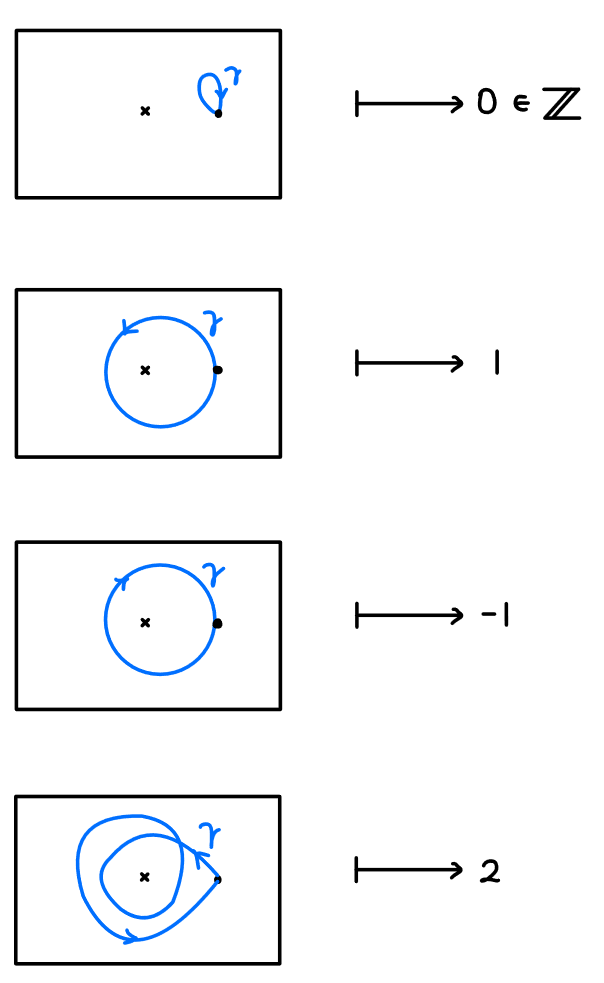
例 如果路径$\gamma$可微,可以定义为
$$\dfrac{1}{2\pi\mathrm{i}}\displaystyle\int_{\gamma}\dfrac{\mathrm{d}z}{z}.\tag*{}$$
例