数学 抽象代数——椭圆曲线
定义 设$f(x)$是一个良好的三次多项式。由$f$定义的椭圆曲线是集合
$$\mathbb{E}:=\{\mathscr{O}\} \cup\left\{(x, y) \mid y^2=f(x)\right\}$$
例 方程$y^{2}=f(x)$的解如下图所示:
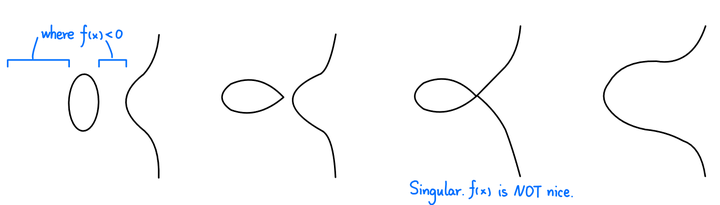
注意$(x,y)\in\mathbb{E} \Rightarrow (x,-y)\in\mathbb{E}$。
定理 每个椭圆曲线都是一个Abel群。
这令人惊讶。我们定义群操作如下:
$$ \begin{aligned} \mathbb{E}\times\mathbb{E}&\to\mathbb{E}\\ (P,Q)&\mapsto P+Q \end{aligned}\tag*{} $$
(1) 如果$P, Q=\mathscr{O}$,则设
$$\mathscr{O}+\mathscr{O}=\mathscr{O}.\tag*{}$$
(2) 如果$P=\mathscr{O}$,$Q=(x,y)\in\mathbb{E}$,则设
$$\mathscr{O}+Q=Q+\mathscr{O}=Q.\tag*{}$$
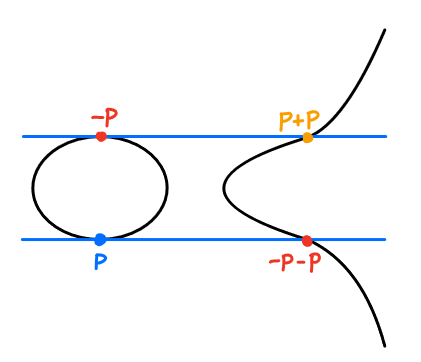
(3) 如果$P$,$Q$属于$\{(x,y)\mid y^{2}=f(x)\}$,考虑包含$P$和$Q$的唯一直线$L_{PQ}$。
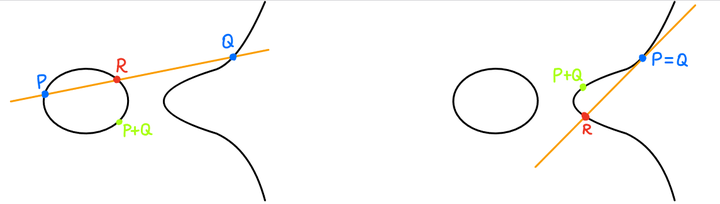
一条直线$L$与三次曲线交于三点。设$R=(x,y)$为第三个交点,则定义$P+Q:=(x,-y)$。
规则:若$L_{PQ}$是垂直线,它在$\mathbb{R}^{2}$中不再有第三个交点,我们定义第三个交点$R$为“无穷远点” $\mathscr{O}$。
(这其实是投影几何中的一种解释,在那里平行线——例如垂直线——在无穷远点相交。)
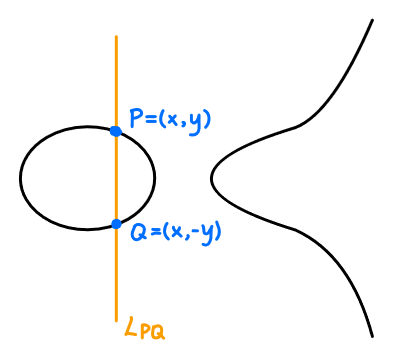
注意$L_{PQ}=L_{QP}$,所以$P+Q=Q+P$。
证明$\mathbb{E}\times\mathbb{E}\to\mathbb{E}$是结合的较为困难。
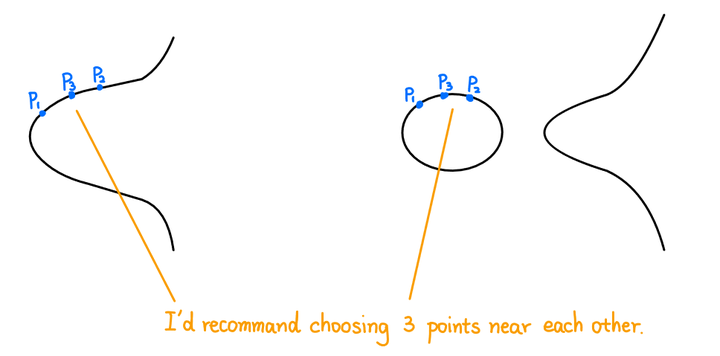
命题 $(P_{1}+P_{2})+P_{3}=P_{1}+(P_{2}+P_{3})$。
一个很棒的观察:假设$f(x)=a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0}$且$a_{i}\in\mathbb{Q}$。若$P, Q\in\mathbb{E}$为有理点(即它们的$x$和$y$坐标为有理数)。那么也是有理点!
证明:$L_{PQ}$的方程为
$$y=mx+t\tag*{}$$
$P, Q\in\mathbb{Q}^{2}\Rightarrow m, t\in\mathbb{Q}$。交点$L_{PQ}\cap\mathbb{E}$包含$R$满足方程
$$(mx+t)^{2}=a_{3}x^{3}+a_{2}x^{2}+a_{1}x+a_{0}\tag*{}$$
$\Rightarrow P, Q, R$是某个有理系数三次多项式$g(x)$的根。
$\Rightarrow$
$$(x-x_{1})(x-x_{2})(x-x_{3})=g(x)=b_{3}x^{3}+b_{2}x^{2}+b_{1}x+b_{0}\tag*{}$$
由于$x_{1}, x_{2}\in\mathbb{Q} \Rightarrow x_{3}\in\mathbb{Q}$,因为$x_{1}x_{2}x_{3}$是$g(x)$的常数项!(更好的是:因为$x_{1}+x_{2}+x_{3}=b_{2}$且$x_{1}, x_{2}, b_{2}\in\mathbb{Q}$。)
$$~\tag*{$\square$}$$
定义 若$f$是有理三次多项式(即$a_{i}\in\mathbb{Q}$),定义$\mathbb{E}(\mathbb{Q})\subset\mathbb{E}$为集合
$$(\mathbb{E}\cap(\mathbb{Q}\times\mathbb{Q}))\cup\{\mathscr{O}\}\tag*{}$$
即所有坐标为有理数的点$P$以及无穷远点$\mathscr{O}$的集合。
因此我们有一个子集
$$\mathbb{E}(\mathbb{Q})\subset\mathbb{E}\tag*{}$$
它在加法下是封闭的。
它在取逆下也是封闭的,因为
$$P=(x,y)\in\mathbb{Q}\times\mathbb{Q}\tag*{}$$
$\Rightarrow$
$$-P=(x,-y)\in\mathbb{Q}\times\mathbb{Q}\tag*{}$$
并且$\mathbb{E}(\mathbb{Q})$包含单位元$\mathscr{O}$,所以
命题 $\mathbb{E}(\mathbb{Q})\subset\mathbb{E}$是一个子群。
定义 若$G$存在一个有限集合$S$以及一个满同态
$$F(S)\to G,\tag*{}$$
则称是有限生成的(finitely generated)。
解析此定义:设$S=\{s_{1},\ldots,s_{n}\}$为有限集合,并且
$$\phi: F(S)\to G\tag*{}$$
是一个满同态。
$\phi$将每个$s_{i}$映射到某个元素
$$g_{i}=\phi(s_{i})\tag*{}$$
$\phi$是满射的,意味着$\forall g\in G$,$\exists$一个词$w$,使得
$$\phi(w)=g\tag*{}$$
即$g$可以表示为$g_{i}$和$g_{i}^{-1}$的有限乘积。
换句话说,存在一个有限集合
$$g_{1},\ldots,g_{n}\in G\tag*{}$$
使得$G$的任意元素都可以用$g_{i}$及其逆元的乘积来表示。
例 任何有限群$G$都是有限生成的。取
$$S=G\tag*{}$$
并定义映射
$$ \begin{aligned} F(S)&\to G\\ g&\mapsto g. \end{aligned}\tag*{} $$
例 任意循环群$G$都是有限生成的。如果
$$G=\langle g\rangle,\tag*{}$$
取$S=\{g\}$,
$$ \begin{aligned} F(S)&\to G\\ g&\mapsto g. \end{aligned}\tag*{} $$
例 任意有限个有限生成群的积也是有限生成的
$$G=G_{1}\times\cdots\times G_{n}.\tag*{}$$
取$G_{i}$的生成集$S_{i}$并定义$S=S_{1}\cup\cdots\cup S_{n}$。如果$\phi_{i}: F(S_{i})\to G_{i}$是满射$\forall i$ ,定义
$$ \begin{aligned} \phi: F(S)&\to G\\ a_{i}&\mapsto(1,\ldots,1,\phi_{i}(a_{i}),1,\ldots,1) \end{aligned}\tag*{} $$
关于椭圆曲线最重要的一个定理是:
定理(Mordell定理) $\mathbb{E}(\mathbb{Q})$是有限生成的。
这一结果令人惊讶——存在一些有理点$P_{1},\ldots,P_{n}\in\mathbb{E}(\mathbb{Q})$,使得任何其他有理点都可以通过这些$P_{i}$的加减法得到。
