几何学院年度特典：帕秋莉讲流形

By    不动的大图书馆——帕秋莉·诺蕾姬

一、说在前面的话

几何通常是十分直观好理解的。一条直线，一个圆，或者一个曲面，一个椭球——看得见，自然好理解。在$\text{Euclid}$空间$\mathbb{R}^n$中，我们可以和任何几何对象五五开。

但不少魔法使在深入修习数学术法时，会发现自己在非$\text{Euclid}$空间中（如球面$S^n$，环面$T^n$等）对几何的处理力不从心。

因此，数学术法大师$\text{Gauss}$，$\text{Riemann}$等人历经几个世纪的努力，引入了非$\text{Euclid}$几何界两大最重要的概念之一：流形，$\text{Manifold}$（另一个概念在近一个世纪后被提出，即概形，$\text{Scheme}$），成为了应对非$\text{Euclid}$几何的一大利器。

如果你想成为一个优秀的魔法使，掌握这些知识是必要的。那现在，博学的我——帕秋莉·诺蕾姬，就应$\text{ACG}$社（$\text{Algebra-Calculus-Geometry}$社）的几何（$\text{Geometry}$）学院之请求，给各位写一篇关于流形的科普。

一、从熟悉的世界开始

2.1  我们熟悉的几何

先来说一说为什么在$\text{Euclid}$空间$\mathbb{R}^n$中我们可以和任何几何对象五五开。在任何$\text{Euclid}$空间中，我们可以用一个实数列$(x_1,x_2,x_3,…,x_n)$来表示一个点的位置。因此，对于任何的几何对象，我们可以用一个参数方程（$\text{Parametric Equation}$）来解析它。有了这种定量的解析，我们就赢了一半，因为其曲率，挠率等性质可以轻而易举的得到。

好，我们考虑一个问题：对于$\mathbb{R}^3$中的一条曲线$L$，解析它的曲率是简单的。那么，如果$\mathbb{R}^3$中的一个球面$S^2$上的一条曲线$\mathcal{L}$，怎么解析它的曲率呢？

好像不那么简单了。

答案是：我们要站在$S^2$的视角上去分析。这就是流形上的几何了。

2.2  流形的初步认识

流形是广义上的几何对象，其局部（$\text{Local}$）相当于我们熟悉的$\text{Euclid}$空间。简单来说，对于流形上的任意一点，都存在一个包含该点的小区域，这个小区域可以通过一个连续的映射与欧几里得空间中的某个区域建立一一对应关系，并且这个映射及其逆映射都是连续的。

如果你还觉得抽象，那我们举一个例子。

以地球表面为例。在$\text{Euclid}$几何中，我们是站在地球之外的某一点进行观察，然后给出地球表面的参数方程：

$$x^{2}+y^2+z^2=\text{Const}$$

满足这个参数方程的点都在地球表面上，包括幻想乡。

但当我们站在地球上的某个地方时，我们本身就在地球上，所以无法总揽全局，会感觉自己身处一个平面。只有当我们考虑较大的范围时，才会意识到地球是一个球体。

从数学的角度来看，对于任地球表面上任意大的范围，只要不闭合，就是与$\mathbb{R}^2$存在一一对应关系的。所以，地球表面就是一个二维流形。

三、流形的标准定义与基本性质

3.1  拓扑流形

一个$n$维拓扑流形（$\text{Topological Manifold}$）$M$是一个满足以下条件的拓扑空间（$\text{Topological}$ $\text{Space}$）：

·$\text{Hausdorff}$性质：对于$M$中任意两个不同的点$p$和$q$，都存在不相交的开集$U$和$V$，使得$p\in U$，$q\in V$。这一性质保证了流形上的点具有良好的分离性。

·局部$\text{Euclid}$性质：对于$M$中的每一个点$p$，都存在一个包含$p$的开子集$U\subseteq M$以及一个同胚（$\text{Homeomorphism}$）映射$\varphi:U\rightarrow \hat{U}$，其中$\hat{U}$是$\mathbb{R}^n$中的一个开子集。同胚映射是一种连续且逆映射也连续的映射，它使得我们可以在局部将流形上的点与欧几里得空间中的点建立起一一对应的关系。这一性质非常重要。

有时候还会加入第二可数性，防止某些过大的曲面无法处理。不过这已经在讲义之外了，这里也就不再介绍了。

3.2  坐标卡与图册

前面提到的拓扑流形的定义中，二元组$(U,\varphi)$被称为一个坐标卡（$\text{Coordinate System}$），$U$是流形$M$上的开子集，$\varphi$是从$U$到$\mathbb{R}^n$中开子集$V$的同胚映射。而一个流形$M$上这样的坐标卡的集合$\{(U_i,\varphi_i)\}_{i\in I}$被称为图册（$\text{Atlas}$），如果它可以构成流形$M$的开覆盖（$\text{Open Cover}$），即

$$M=\bigcup_{i\in I}U_i$$

图册，顾名思义，直观上理解就是流形的地图册。一个坐标卡相当于一张地图，而一个图册给流形的每一个局部一张地图，即一种描述点的方法。具体而言，对于流形上的点$p$，在某一包含$p$的容许坐标卡$(U,\varphi)$下，$p$的第$\mu$个坐标（$\text{Coordinate}$）定义为

$$u^\mu(p)=(\varphi^{-1}(p))^\mu$$

这里$\mu$不是幂，而是指标。至于为什么这么写请自行查询。

上述坐标的定义适用于全体$p\in U$。由此可以诱导出$U$上的一个坐标系$(U;(u^\mu))$，称$M$上由$(U,\varphi)$诱导的一个局部坐标系（$\text{Local}$ $\text{Coordinate System}$）。这样我们就完美的把$\text{Euclid}$空间中“坐标”的概念推广到流形几何学上。

3.3  光滑流形与微分流形

如果流形$M$上的图册$\{(U_i,\varphi_i)\}_{i\in I}$满足：当$U_i\cap U_j\neq\varnothing$时，映射

$$\varphi_j\circ\varphi_i^{-1}:\varphi_i(U_i\cap U_j)\rightarrow\varphi_j(U_i\cap U_j)$$

是光滑的，那么$M$被称为一个光滑流形（$\text{Smooth Manifold}$）。光滑流形是流形分析学中研究的主要对象之一，因为光滑性使我们可以用微积分。

那么，上面这个复合映射有什么几何意义呢？

对，坐标变换。不同局部坐标系之间的坐标变换。或者可以理解为不同地图上的位置之间的转换。也就是说，光滑流形的所有局部坐标系之间的坐标变换都是光滑的。

光滑流形$M$上全体与对方相容的（即相互之间的坐标变换是$C^\infty$的）坐标卡构成的图册（也就是所谓的$C^\infty$类极大微分图册）$\mathcal{D}$称$M$的$C^\infty$类微分结构（$\text{Differential Structure}$）。配备了$C^\infty$类微分结构的流形，即二元组$(M,\mathcal{D})$称为一个$C^\infty$类微分流形（$\text{Differential Manifold}$）。

更广义的，如果在某一拓扑流形$M$上，存在图册$\mathcal{D}$满足任意$\mathcal{D}$中坐标卡之间的变换是具有直到$k$阶连续偏导的（即$C^k$类微分映射），且任意与$\mathcal{D}$中坐标卡$C^k$相容的（即相互之间的坐标变换是$C^k$的）坐标卡均在$\mathcal{D}$内，就称$\mathcal{D}$为一个$C^k$类微分结构，称二元组$(M,\mathcal{D})$为一个$C^k$类微分流形。

不较真的话，光滑流形和$C^\infty$类微分流形是一样的。

四、切空间与切向量

4.1  切向量的回顾

在$\text{Euclid}$空间中，引入切向量是直观和自然的。想象在$\text{Euclid}$空间中的一条正则参数曲线$\vec{r}(\lambda)$通过某一曲面上的点$p$，那么这条曲线在$p$点就有一个切向量：

$$\vec{v}=\frac{d\vec{r}}{d\lambda}\bigg|_p$$

$$=\left(\frac{\partial\vec{r}}{\partial x_i}\frac{dx_i}{d\lambda}\right)\bigg|_p$$

4.2  切向量在光滑流形和一般流形上的严格定义

设$M$是一个光滑流形，$p\in M$。一条光滑曲线

$$\gamma:(-\epsilon,\epsilon)\rightarrow M$$

满足$\gamma(0)=p$。定义曲线$\gamma$在$p$点的切向量为

$$\vec{v}=\frac{d\gamma(\lambda)}{d\lambda}\bigg|_{\lambda=0}$$

更一般地，在$n$维拓扑流形上，$p$的一个切向量$\vec{v}$定义为一个包含$p$的容许坐标卡$(U_i,\varphi_i)$下的一个数组$(v^1_i,v^2_i,…,v^n_i)$，并且当$(U_i,\varphi_i)$，$(U_j,\varphi_j)$是两个包含$p$的容许坐标卡时，对应数组$(v^1_i,v^2_i,…,v^n_i)$和$(v^1_j,v^2_j,…,v^n_j)$满足方程

$$v_j^\alpha = v_i^\beta \frac{\partial u_j^\alpha}{\partial u_i^\beta}\bigg|_p$$

式中使用了$\text{Einstein}$求和约定（$\text{Einstein summation convention}$），其中$\beta$是哑指标，$\alpha$是自由指标，$i,j$是普通指标，仅作标记坐标卡之用，不求和。

从张量的角度来看，所谓切向量实则是流形上的一阶张量（$\text{Tensor}$）的统称，而其“对应数组”$(v^1,v^2)$是一阶张量的逆变分量（$\text{Contra-variant}$ $\text{Component}$）组，满足逆变分量变换关系。

$p$点处全体切向量的集合构成一个向量空间，称为$M$在$p$点的切空间（$\text{Tengent Space}$），记为$T_pM$。

4.3  切空间的基

对于一个向量空间而言，“基”是必须存在的。相应的，切空间$T_pM$也存在基。

设$(U,\varphi)$是包含$p$点的一个坐标卡，则根据流形上坐标的定义，我们有

$$\varphi(p)=(u^1(p),u^2(p),\cdots,u^n(p))$$

对于$i=1,\cdots,n$，定义曲线族

$$\gamma_\mu(\lambda)=\varphi^{-1}(u^1(p),\cdots,u^\mu(p)+\lambda,\cdots,u^\mu(p))$$

那么${\gamma_1'(0),\cdots,\gamma_n'(0)}$，即这一曲线族在$p$的切向量构成$T_pM$的一组基（$\text{Basis}$），记为
$$\{\frac{\partial}{\partial u^1}\bigg|_p,\cdots,\frac{\partial}{\partial u^n}\bigg|_p\}$$

另一种更加高调，也更严格的定义是微分算子定义。流形上$p$点的切向量可以解释为微分算子

$$\hat{v}:C^\infty(U)\rightarrow \mathbb{R}$$

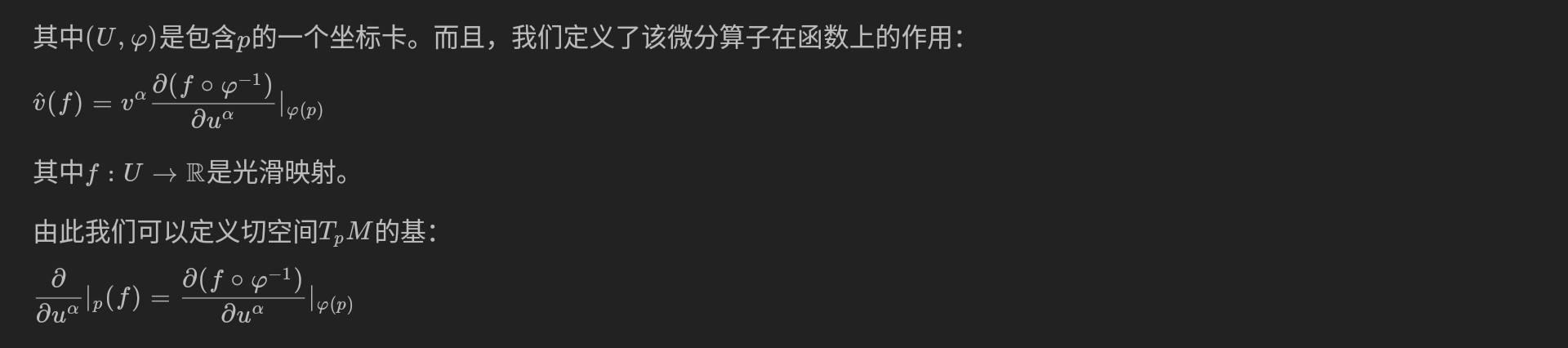
其中$(U,\varphi)$是包含$p$的一个坐标卡。而且，我们定义了该微分算子在函数上的作用：

$$\hat{v}(f)=v^\alpha\frac{\partial(f\circ \varphi^{-1})}{\partial u^\alpha}\bigg|_{\varphi(p)}$$

其中$f:U\rightarrow \mathbb{R}$是光滑映射。

由此我们可以定义切空间$T_pM$的基：

$$\frac{\partial}{\partial u^\alpha}\bigg|_p(f)=\frac{\partial(f\circ \varphi^{-1})}{\partial u^\alpha}\bigg|_{\varphi(p)}$$

等式右边为$\mathbb{R}^n$中的普通偏导数，$f$是任意在$U$内有定义的光滑函数。

$\{\frac{\partial}{\partial u^\mu}\big|_p\}$称为由$(U,\varphi)$诱导的自然基（$\text{Natural Basis}$）。

显然，$\{\frac{\partial}{\partial u^\mu}\big|_p\}$对应的数组在第$\mu$位是$1$，其余位置均为$0$。因此，$\{p;\frac{\partial}{\partial u^\mu}\big|_p\}$构成$U$上的一个标架场（$\text{Frame Field}$），称由$(U,\varphi)$诱导的自然标架场（$\text{Natural}$ $\text{Frame Field}$）。

五、余切空间与余切向量

5.1  余切向量

$p$点处的余切向量（$\text{Cotengent Vector}$）是切空间$T_pM$上的线性泛函。也就是说，余切向量是这么一个线性映射：

$$\text{Cotengent Vector}:T_pM\rightarrow \mathbb{R}$$

$p$点处所有余切向量的集合构成一个向量空间，称为$M$在$p$点的余切空间，记为$T_p^*M$。

明显地我们看到，$T_p^*M$是$T_pM$的对偶空间。

5.2  余切空间的基

在高等代数中我们都学习过，一个向量空间的对偶空间也是向量空间，也有其自身的基，称对偶基（$\text{Dual Basis}$）。同样，余切空间$T_p^*M$也有基。现在我们就尝试来找它的基。

考虑流形$M$上一个包含$p$的坐标卡$(U,\varphi)$。设$\{\frac{\partial}{\partial u^\mu}|_p\}$是$T_pM$的一组基。考虑基在坐标

$$u^\nu:U\rightarrow \mathbb{R}$$

上的作用

$$\frac{\partial}{\partial u^\mu}\bigg|_p(u^\nu)=\frac{\partial(u^\nu\circ \varphi^{-1})}{\partial u^\mu}\bigg|_{\varphi(p)}$$

其中复合映射

$$u^\nu\circ \varphi^{-1}:\mathbb{R}^n\rightarrow \mathbb{R}$$

明显只是$\mathbb{R}^n$中的普通坐标。

前面提到过，切向量作为微分算子时，等式右边只是$\mathbb{R}^n$中的普通偏导数。所以在$\mathbb{R}^n$坐标下，等式右边偏导数上下两个函数的作用实则只是取$\mathbb{R}^n$中同一点的两个坐标。那么就有

$$\frac{\partial}{\partial u^\mu}\bigg|_p(u^\nu)=\delta^\nu_\mu$$

又根据大家喜闻乐见的高数中的公式

$$du^\nu|_p\left(\frac{\partial}{\partial u^\mu}\bigg|_p\right)=\frac{\partial}{\partial u^\mu}\bigg|_p(u^\nu)$$

即得

$$du^\nu|_p\left(\frac{\partial}{\partial u^\mu}\bigg|_p\right)=\delta^\nu_\mu$$

于是乎，根据定义我们发现，$\{du^\mu|_p\}$构成$T_pM$基的一组对偶基，也就是说$\{du^\mu|_p\}$就是$T_p^*M$的基。这样我们就把它找到了。

余切向量在流形几何学中的地位非常重要，因为它涉及外微分这个重要概念。

六、微分形式

6.1  微分形式的定义

接下来的概念比较难，我们简单介绍。有兴趣的魔法使们可以自行学习。在此推荐陈维桓教授所著的《微分几何》和杜武亮教授所著《流形导论》作为参考书。

一个$k$次微分形式$\omega$是一个反对称的$k$重线性映射，它将每一个点$p\in M$处的$k$个切向量映射到实数域$\mathbb{R}$。即对于

$$X_1,\cdots,X_k\in T_pM$$

$$\omega_p(X_1,\cdots,X_k)\in\mathbb{R}$$

并且满足反对称性：

$$\omega_p(X_{\sigma(1)},\cdots,X_{\sigma(k)})=\text{sign}(\sigma)\omega_p(X_1,\cdots,X_k)$$

其中$\sigma$是${1,\cdots,k}$的一个置换。

6.2  外微分

外微分是一种将$k$次微分形式映射到$(k + 1)$次微分形式的算子，记为$d$。外微分满足一些重要的性质，例如$d^2 = 0$。即对一个微分形式进行两次外微分得到零形式。外微分在流形分析中有着广泛的应用，它与流形上的积分理论密切相关。著名的$\text{de Rham}$复形就是外微分导出的。

七、流形上的积分

7.1  定向流形

一个流形$M$被称为定向流形，如果存在一个由坐标卡$\{(U_i,\varphi_i)\}_{i\in I}$组成的图册，使得当$U_i\cap U_j\neq\varnothing$时，映射$\varphi_j\circ\varphi_i^{-1}$的$\text{Jacobi}$行列式恒大于零。定向性是积分的一个重要的前提条件，它类似于我们在欧几里得空间中对积分方向的规定。

7.2  $n$维流形上的$n$次微分形式的积分方法

设$M$是一个定向的$n$维流形，$\omega$是$M$上具有紧支集的$n$次微分形式。我们可以通过将$M$用坐标卡覆盖，并利用坐标卡将$\omega$拉回到$\mathbb{R}^n$上进行积分，然后将这些局部积分相加来定义$\omega$在$M$上的积分$\int_M\omega$。

7.3  $\text{Stokes}$定理

斯托克斯定理是流形上积分的一个重要定理，其将流形上的外微分和边界上的积分联系起来。

设$M$是一个具有边界$\partial M$的定向$n$维流形，$\omega$是$M$上的一个$(n - 1)$次微分形式，则

$$\int_Md\omega=\int_{\partial M}\omega$$

斯托克斯定理是$\text{Newton-Lebnitz}$定理在流形上的推广。

八、结语

本文仅作为科普。微分几何的学习路径有两条：

第一条，几何线，研究光滑流形，外微分，纤维丛，$\text{de Rham}$复形，范畴论， $\text{Atiyah-Singer}$指标定理等。

第二条，分析线，研究度量，$\text{Riemann}$流形，$\text{Lie}$导数，$\text{Lie}$群，曲率张量，$\text{Ricci}$流等。

本文只是几何线中最浅显的概念的一个简介。如果你感兴趣，请离开本文，买几本书，继续深入下去。

哦，对了，别忘了带你入坑的是幻想乡的魔法使帕秋莉·诺蕾姬。