质

物理

积分术法（Oλοκλήρωση Μαγεία）原典（卷四）

积分术法（Oλοκλήρωση Μαγεία）原典

自由基注：2025.5.3，我对积分术法进行了修订，修改了一些无法显示的错误内容。

零、写在正文前的话

本书是积分术法（Oλοκλήρωση Μαγεία）的原典。本原典是由活性自由基（AFR，英语全名Active Free Radical，希腊语名δραστικός ελεύθερος ρίζα）汇总历代大师在积分方面的50项研究成果而成的。原典的原文由希腊语撰写，并由ἄπειρον学派成员37（英文全名Thirty-Seven，希腊语名Τριάντα-Επτά）译成汉语。

本卷是原典的第三卷，收录了第十一，十二章，第三十到三十二种积分术法。

十一、奇异积分术法

不合群的奇点会被踢出积分域。

（三十）$\text{Cauchy}$主值积分术

1.原理：（$\text{Cauchy}$三杀）这是本典中第十二个高级术法。

$\text{Cauchy}$主值是处理奇异积分的重要概念，也是奇异积分算子理论不可绕过的一部分。对于积分

$$\int_{a}^{b}f(x)dx$$

当函数$f(x)$在区间$[a,b]$内某点$c$处存在奇点（使得函数在此点无界等情况）时，常规积分可能不存在。若$c\in(a,b)$是奇点，$\text{Cauchy}$主值

$$\text{p.v.}\int_{a}^{b}f(x)dx$$

定义为$$\lim_{\epsilon \to 0^{+}}[\int_{a}^{c - \epsilon}f(x)dx + \int_{c + \epsilon}^{b}f(x)dx]$$

其避开了奇点处直接积分的困境，为研究奇异积分处理提供了有效的途径。

2.示例：考虑积分

$$\int_{-1}^{1}\frac{1}{x}dx$$

$x = 0$是函数$f(x)=\frac{1}{x}$的奇点。按照柯西主值的计算方法，

$$\text{p.v.}\int_{-1}^{1}\frac{1}{x}dx = \lim_{\epsilon \to 0^{+}}[\int_{-1}^{-\epsilon}\frac{1}{x}dx + \int_{\epsilon}^{1}\frac{1}{x}dx]$$

计算可得

$$\lim_{\epsilon \to 0^{+}}[\ln \epsilon - \ln 1 + \ln 1 - \ln \epsilon]=0$$

（三十一）$\text{Hadamard}$有限部分积分术

1.原理：这是本典中第十三个高级术法。

本术法由解析数论和分析学大师$\text{Jacques Solomon Hadamard}$开发。

$\text{Hadamard}$有限部分积分术是处理含强奇异积分的一种重要术法，当积分

$$\int_{a}^{b}f(x)dx$$

中的被积函数$f(x)$在积分区间$[a,b]$内某点$c$处存在强奇点（即函数在该点附近的无界性更为剧烈，导致常规积分与柯西主值积分方法失效）时，$\text{Hadamard}$有限部分积分术定义为：

设$f(x)$在$[a,b]$上除$x = c\in(a,b)$外连续，且在$x = c$附近具有形如$\frac{g(x)}{(x - c)^n}$，（$n\gt1$，$g(x)$在$c$点邻域连续且$g(c)\neq0$）的强奇异性。将积分

$$\int_{a}^{b}f(x)dx$$

在奇点$c$附近进行处理（如$\text{Taylor}$展开），然后对展开式进行积分运算，舍弃掉其中发散的部分，剩余的有限部分就定义为$\text{Hadamard}$有限部分积分，记为

$$\text{f.p.}\int_{a}^{b}f(x)dx$$

这种术法通过对积分进行特殊的解析延拓处理，巧妙地将原积分分解为一个有限部分和一个发散部分，以此来处理强奇异积分问题。

2.示例：考虑积分

$$\int_{0}^{1}\frac{1}{x^{2}}dx$$

$x = 0$是函数$f(x)=\frac{1}{x^{2}}$的强奇点。按照$\text{Hadamard}$有限部分积分术，我们先对积分进行处理。设

$$I(\epsilon)=\int_{\epsilon}^{1}\frac{1}{x^{2}}dx$$

计算可得

$$I(\epsilon)=-1+\frac{1}{\epsilon}$$

在这里，$\frac{1}{\epsilon}$是随着$\epsilon\to0$ 而发散的部分，而有限部分为$-1)$，所以该积分的$\text{Hadamard}$有限部分积分的值为$-1$ ，即

$$\text{f.p.}\int_{0}^{1}\frac{1}{x^{2}}dx = -1$$

十二、实变积分估计术法

现在才是真正的数学嘛。

（三十二）$\text{Hardy-Littlewood}$极大函数积分术

1.原理：

$\text{Hardy-Littlewood}$极大函数是调和分析中的重要概念，由两位数论和分析学大师$\text{Godfrey Hardy}$和$\text{John Edensor Littlewood}$共同提出。

本典中第十四个高级术法。

设$f(x)$是$\mathbb{R}^n$上的局部可积函数，即$f\in L^1_{\text{loc}}(\mathbb{R}^n)$，$\text{Hardy-Littlewood}$极大函数$Mf(x)$定义为

其中$\mathbb{B}(x,r)$是以$x$为中心，$r$为半径的球，$|\mathbb{B}(x,r)|$表示球$\mathbb{B}(x,r)$的体积（或测度）。

定义表明，$Mf(x)$是通过对$f(x)$在以$x$为中心的不同半径的球上的积分取平均的上确界得到的。

$Mf(x)$具有许多优良性质。除基本性质（非负，齐次，单调）之外，有如下性质：

·弱$(1,1)$型性

$Mf(x)$是弱$(1,1)$型。即$Mf(x)$满足，存在常数$C$大于零使得对于任意$\lambda$大于零，$f\in L^1(\mathbb{R}^n)$，有

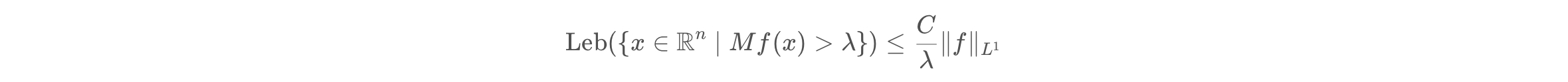
$\text{Leb}$表示$\text{Lebesgue}$测度。

这是$\text{Hardy-Littlewood}$极大函数最重要的性质没有之一。几乎所有关于$\text{Hardy-Littlewood}$极大函数的不等式都是用这条性质推导的。

这条性质可以使用$\text{Vitali}$覆盖引理证明。证明过程已经超出本典范围，有兴趣者可以自行查询。

· $L^p$有界性

对于$1<p\leq\infty$，如果$f\in L^p(\mathbb{R}^n)$则$Mf\in L^p(\mathbb{R}^n)$，且$Mf$是$L^p(\mathbb{R}^n)$到$L^p(\mathbb{R}^n)$有界的，即存在常数$C_p>0$使不等式

$$\|Mf\|_{L^p}\leq C_p\|f\|_{L^p}$$

恒成立。

这条性质也非常重要。这表明$\text{Hardy-Littlewood}$极大函数本质上是$L^p(\mathbb{R}^n)$上的有界算子

$$M: L^p(\mathbb{R}^n)\rightarrow L^p(\mathbb{R}^n)$$

该性质可以由弱$(1,1)$型不等式和$\text{Marcinkiewicz}$插值，或使用$\text{Calderón-Zygmund}$分解证明，这里一样不演示。

·下半连续性

$Mf$是下半连续的。即对于$\forall\lambda\in \mathbb{R}$，集合

是开的。

这个性质还蛮好证的，可以试着证明一下。

·卷积性

不等式

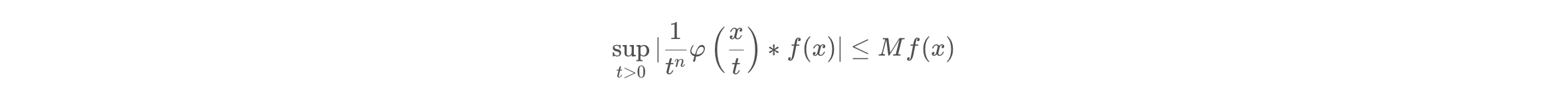
对于所有满足全局归一性

$$\int_{\mathbb{R}^n}\varphi(x)dx=1$$

的$\varphi\in L^1(\mathbb{R}^n)$成立。

这个就别管怎么证明了，不好证。

·几乎处处逐点控制性

对于$\forall f\in L^1_{\text{loc}}(\mathbb{R}^n)$，

$$|f(x)|\leq Mf(x)$$

几乎处处成立。

这就告诉我们为什么它叫“极大函数”。

这条性质是非常好证明的：

 证毕。

2.示例：试证$\text{Hardy-Littlewood-Sobolev}$不等式（$\text{HLS}$不等式）：

$$\|I_\alpha f\|_{L^q} \leq C\|f\|_{L^p}$$

其中$f\in L^p(\mathbb{R}^n)$，$\frac{1}{q} = \frac{1}{p} - \frac{\alpha}{n}$，$I_\alpha$是$\text{Risez}$位势，定义为

$$I_\alpha f(x) = \int_{\mathbb{R}^n} \frac{f(y)}{|x-y|^{n-\alpha}}dy$$

将$I_\alpha f$分解为两部分：

其中$R > 0$是一个待定的参数。

对于$|x-y| \leq R$，利用$\text{Hardy-Littlewood}$极大函数的定义：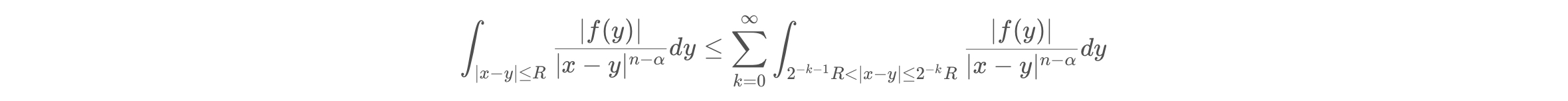

在每一层$2^{-k-1}R$小于$|x-y|$小于等于$2^{-k}R$，有

$$\frac{1}{|x-y|^{n-\alpha}} \leq \frac{1}{(2^{-k-1}R)^{n-\alpha}}$$

因此：

$$\int_{|x-y| \leq R} \frac{|f(y)|}{|x-y|^{n-\alpha}} \, dy \leq C \sum_{k=0}^\infty (2^{-k}R)^{\alpha} \cdot \frac{1}{|B_{2^{-k}R}(x)|} \int_{B_{2^{-k}R}(x)} |f(y)| \, dy$$

进一步估计为：

$$\int_{|x-y| \leq R} \frac{|f(y)|}{|x-y|^{n-\alpha}} \, dy \leq C R^\alpha Mf(x)$$

对于$|x-y|$大于$R$，利用$\text{Hölder}$不等式：

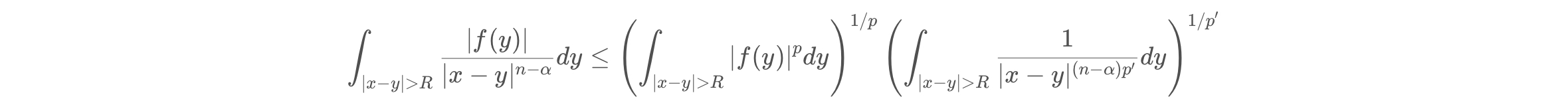
其中$p' = \frac{p}{p-1}$是$p$的共轭指数。计算第二个积分：

$$\int_{|x-y| > R} \frac{1}{|x-y|^{(n-\alpha)p'}}dy = C R^{n - (n-\alpha)p'}$$

因此：

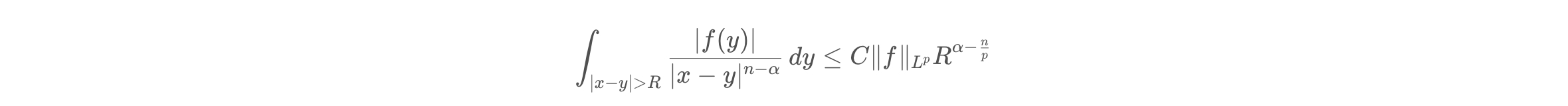
则有

$$|I_\alpha f(x)| \leq C \left( R^\alpha Mf(x) + \|f\|_{L^p} R^{\alpha - \frac{n}{p}} \right)$$

选择$R$使得两项平衡，即：

$$R^\alpha Mf(x) = \|f\|_{L^p} R^{\alpha - \frac{n}{p}}$$

解得：

$$R = \left( \frac{\|f\|_{L^p}}{Mf(x)} \right)^{\frac{p}{n}}$$

代入后得到：
$$|I_\alpha f(x)| \leq C \left( Mf(x) \right)^{1 - \frac{\alpha p}{n}} \|f\|_{L^p}^{\frac{\alpha p}{n}}$$

根据定$\frac{1}{q} = \frac{1}{p} - \frac{\alpha}{n}$，有：

$$\|I_\alpha f\|_{L^q} \leq C \|f\|_{L^p}$$

证毕。

十三、结语

本典到这里就结束了。但我希望读者对积分的研究到这里不会结束。我们仍然有很多问题没有解决，比如，正切函数和正割函数是否存在万能代换术？奇异积分是否存在不剔除奇点的解决方式？甚至读者可以深入分析学，解决诸如非光滑核奇异积分，加权积分估计等深奥难题。我们的旅行才刚到起点。

最后，感谢你的阅读。

谢谢。

（卷四完）