- 时间正序
- 时间倒序
- 评论最多
- 1
第三题明显Taylor啊,应该可以用e的定义式展开吧》》![]() (如果证必要性的可以用话两边求导都一样来证)(证一遍泰勒应该也可以)还有我一个物竞生考我数学有点过分了啊!!~~
(如果证必要性的可以用话两边求导都一样来证)(证一遍泰勒应该也可以)还有我一个物竞生考我数学有点过分了啊!!~~
1.若$\lim\limits_{n\to \infty}a_{n}=a$,则$\lim\limits_{n\to\infty}\dfrac{a_{1}+a_{2}+\cdots+a_{n}}{n}=a$.
证明:$\lim\limits_{n\to\infty}a_{n}=a$ $\Leftrightarrow$ $\forall \varepsilon>0$,$\exists N\in\mathbb{N}_{+}$,当$n>N$时
$$|a_{n}-a|<\varepsilon.$$
令$S_{n}=\sum\limits_{i=1}^{n}a_{i}$,则我们可以将求和分成两部分
$$\dfrac{S_{n}}{n}=\dfrac{1}{n}\sum\limits_{i=1}^{n}a_{i}=\dfrac{1}{n}\sum\limits_{i=1}^{N}a_{i}+\dfrac{1}{n}\sum\limits_{i=N+1}^{n}a_{i}$$
其中,第一部分$\dfrac{1}{n}\sum\limits_{i=1}^{N}a_{i}$是一个常数(因为$N$是有限值),对其取极限$n\to\infty$有
$$\lim\limits_{n\to\infty}\dfrac{1}{n}\sum\limits_{i=1}^{N}a_{i}=\lim\limits_{n\to\infty}\dfrac{C}{n}=0\tag{1}$$
对于第二部分,我们有
$$\begin{aligned}\dfrac{1}{n}\sum\limits_{i=N+1}^{n}a_{i}&=\dfrac{1}{n}\sum\limits_{i=N+1}^{n}[a+(a_{i}-a)]\\&=\dfrac{1}{n}\sum\limits_{i=N+1}^{n}a+\dfrac{1}{n}\sum\limits_{i=N+1}^{n}(a_{i}-a)\\&=\dfrac{n-N}{n}a+\dfrac{1}{n}\sum\limits_{i=N+1}^{n}(a_{i}-a)\end{aligned}$$
对其取极限得
$$\begin{aligned}\lim\limits_{n\to\infty}\dfrac{1}{n}\sum\limits_{i=N+1}^{n}a_{i}&=\lim\limits_{n\to\infty}\dfrac{n-N}{n}a+\lim\limits_{n\to\infty}\dfrac{1}{n}\sum\limits_{i=N+1}^{n}(a_{i}-a)\\&=a+\lim\limits_{n\to\infty}\dfrac{n-N}{n}\varepsilon\\&=a+0\\&=a\end{aligned}\tag{2}$$
(1)+(2)两边分别相加即得到结论
$$\lim\limits_{n\to\infty}\dfrac{S_{n}}{n}=0+a=a$$
$$~\tag*{$\square$}$$
2. 取$0<\varepsilon<\varepsilon_{0}$和一个紧区间$I=[t_{0},R]$。已知$S: I\to [0,+\infty)$是一个非负不减函数且满足$S(t_{0})=0$和
$$S(T)\leqslant\varepsilon_{0}(S(T)+\varepsilon)^{4}+\varepsilon_{0}^{4}(S(T)+\varepsilon)+\varepsilon_{0}(S(T)+\varepsilon)^{5},\qquad \forall T\in I$$
若$\varepsilon_{0}$可选定任意小,证明:对任意$T\in I$,$S(T)\leqslant \varepsilon$成立。
先来略微说一下证明思路。若想证明对所有$T\in I$都有$S(T)\leqslant\varepsilon$,常见的做法是反证法:假设存在某个时刻$T\in I$使得$S(T)>\varepsilon$。由于$S$是从$0$开始的单调不减函数,那么令
$$T^{*} = \inf\{\,t \in [t_{0}, R]\mid S(t)\geqslant \varepsilon\}.$$
因为$S$单调不减且初值$S(t_{0})=0$,我们可以断言在$T^{*}$处函数首次“触及”或“超过”$\varepsilon$,并有(在适当的连续性条件下)
$$S(T^{*}) = \varepsilon.$$
在$t=T^{*}$带入给定的不等式,争取得到与$\varepsilon\leqslant\cdots$矛盾,从而推出假设不可能成立。
证明:使用反证法证明。假设结论不成立,则必存在$T_{1}\in I$使得
$$S(T_{1}) > \varepsilon.$$
由于$S$单调不减且$S(t_{0})=0$,定义
$$T^{*} = \inf\{\,t \in [t_{0}, R]\mid S(t)\geqslant \varepsilon\}.$$
可得
$$S(T^{*}) = \varepsilon\quad \bigl(\text{在首次触及处连续时}\bigr).$$
根据题设,不等式
$$S(T)\leqslant \varepsilon_{0}\bigl(S(T)+\varepsilon\bigr)^{4}\;+\;\varepsilon_{0}^{4}\bigl(S(T)+\varepsilon\bigr)\;+\;\varepsilon_{0}\bigl(S(T)+\varepsilon\bigr)^{5}$$
对所有$T\in [t_{0}, R]$成立,故对$T^{*}$亦成立。此时由于
$$S(T^{*}) = \varepsilon,\quad S(T^{*}) + \varepsilon = 2\varepsilon,$$
得到
$$\varepsilon\;=\;S(T^{*})\;\leqslant\;\varepsilon_{0}\,(2\varepsilon)^{4}\;+\;\varepsilon_{0}^{4}\,(2\varepsilon)\;+\;\varepsilon_{0}\,(2\varepsilon)^{5}.$$
即
$$\varepsilon\;\leqslant\;\varepsilon_{0}\,16\,\varepsilon^{4}\;+\;\varepsilon_{0}^{4}\,\bigl(2\varepsilon\bigr)\;+\;\varepsilon_{0}\,32\,\varepsilon^{5}.$$
观察上式右边,可将其视为对$\varepsilon_{0}$的多项式(并带有系数均为$\varepsilon$的幂)。当$\varepsilon_{0}$充分小时,右边显然可以被压到比$\varepsilon$更小的数值上。
换言之,我们可以令$\varepsilon_{0}$满足
$$\varepsilon_{0}\,16\,\varepsilon^{4}\;+\;\varepsilon_{0}^{4}\,\bigl(2\varepsilon\bigr)\;+\;\varepsilon_{0}\,32\,\varepsilon^{5}\;<\;\varepsilon.$$
则得到
$$\varepsilon \;\leqslant\; \text{(右边)} \;<\; \varepsilon,$$
这与$\varepsilon \leqslant \dots < \varepsilon$明显矛盾。
综上,假设“存在$T$使$S(T)>\varepsilon$”必然导出矛盾,因此只能有
$$\forall\,T \in [t_{0},R], \quad S(T)\;\leqslant\;\varepsilon.$$
$$~\tag*{$\square$}$$$
3. 令$P_{n}(x)=1+x+\dfrac{x^{2}}{2!}+\cdots+\dfrac{x^{n}}{n!}$,证明:$\lim\limits_{n\to\infty}P_{n}(x)=\mathrm{e}^{x}$。
这题主要问题不在Taylor展开上,主要在于对于余项极限的估计。
证明:已知
$$P_{n}(x)=\sum\limits_{k=0}^{n}\dfrac{x^{k}}{k!}$$
而$\mathrm{e}^{x}$的幂级数展开为
$$\mathrm{e}^{x}=\sum\limits_{k=0}^{\infty}\dfrac{x^{k}}{k!}$$
两者相差为
$$\mathrm{e}^{x}-P_{n}(x)=\sum\limits_{k=n+1}^{\infty}\dfrac{x^{k}}{k!}\tag{$\star$}$$
使用绝对值估计
$$\left|\sum\limits_{k=n+1}^{\infty}\dfrac{x^{k}}{k!}\right|\leqslant \dfrac{|x|^{n+1}}{(n+1)!}\left(1+\dfrac{|x|}{n+2}+\dfrac{|x|^{2}}{(n+2)(n+3)}+\cdots\right)$$
当$n\to\infty$时,$\dfrac{x^{n+1}}{(n+1)!}\to 0$,故
$$\lim\limits_{n\to\infty}\sum\limits_{k=n+1}^{\infty}\dfrac{x^{k}}{k!}=0$$
因此对($\star$)两边取极限$n\to\infty$
$$\lim_{n\to\infty}[\mathrm{e}^{x}-P_{n}(x)]=0$$
即
$$\lim_{n\to\infty}P_{n}(x)=\mathrm{e}^{x}$$
黄色那页,第一个,用绝对值不等式放缩然后极限运算法
第二个,用单调性,放缩和极限的思想做,设ST然后用S非负不增结合epsilon可以任意小,然后反证推出来
你这样想:
贪心的本质就是取局部最优解
例:
有一个平面直角坐标系
上面有一些格点
你从原点出发,只能沿x=k或y=k移动(k为整数)
要求每个点都要走到至少一遍,求最短路程
你可以自己琢磨琢磨
回头告诉我你的策略
这是一道莫队的前置题目


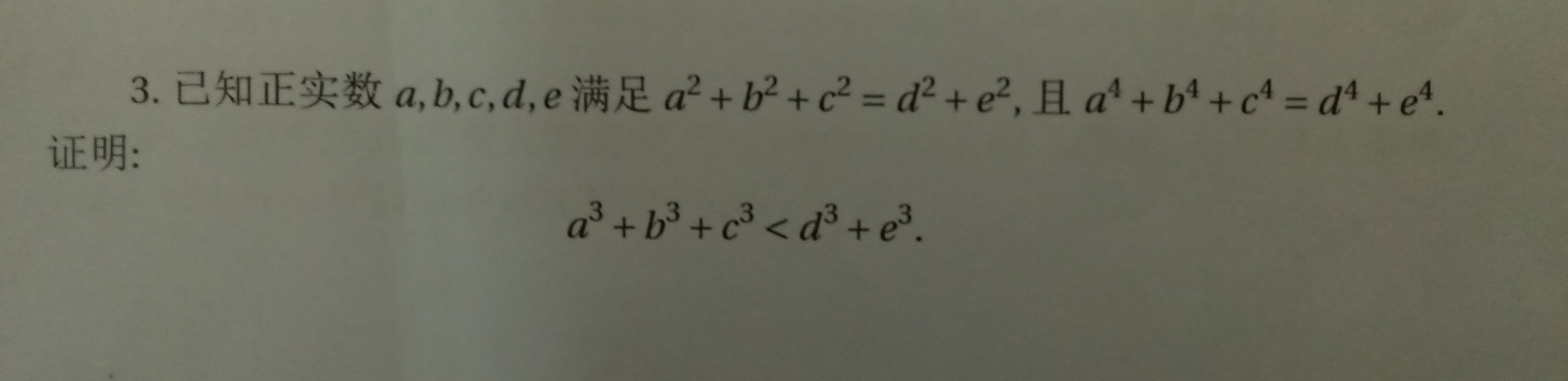



 先给你把思路放这,我先上课了
先给你把思路放这,我先上课了