物理 中国剩余定理
今天听了徐老师的课,突发奇想,同时为了减少论坛水量,决定自己来更一篇
中国剩余定理的定义:假设$m_1,m_2, ...,m_n$是两两互质的正整数,给定同余方程组:
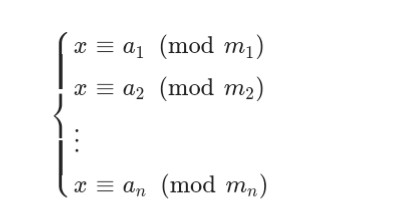 ($LaTeX$还是太麻烦了)
($LaTeX$还是太麻烦了)
中国剩余定理说明当这个同余方程组有解时,可以解得如下的模$m_1 \cdot m_2 \cdot \ldots \cdot m_n$下的唯一解。
人话,中国剩余定理决定了这个同余方程组的存在性,并给解一个构造手段,所以在讨论这种问题时就不再需要解同余方程组,而是借助中国剩余定理证明某个满足一组同余性质的整数存在性。
因此我们可以判定在模不互素时上述同余方程组不一定有解。
但如果在有解的情况下,方程组可以转化为一个互素模的方程组.
在此我总结出3+3个性质
1.在同余方程组中,若不同方程的模两两互素则方程组一定有解;反之,模两两不互素时方程组可能无解
2.在同余方程组中,
共2条回复
时间正序

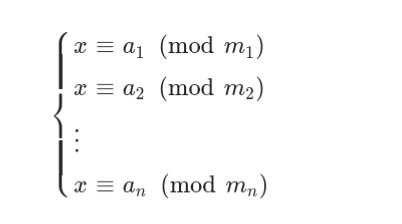 请问如何调校?
请问如何调校?