数学

【二试几何】平面几何定理专题

本帖可用于平几复习或练手

沢（zé）山定理

凸四边形$ABCD$内接于圆$\Gamma $，与边$BC$相交的一个圆与$\Gamma $相切，且分别与$BD$，$AC$切于点$P$、$Q$，则$Q$，则$ \triangle ABC$的内心与$ \triangle DBC$的内心均在直线$PQ$上

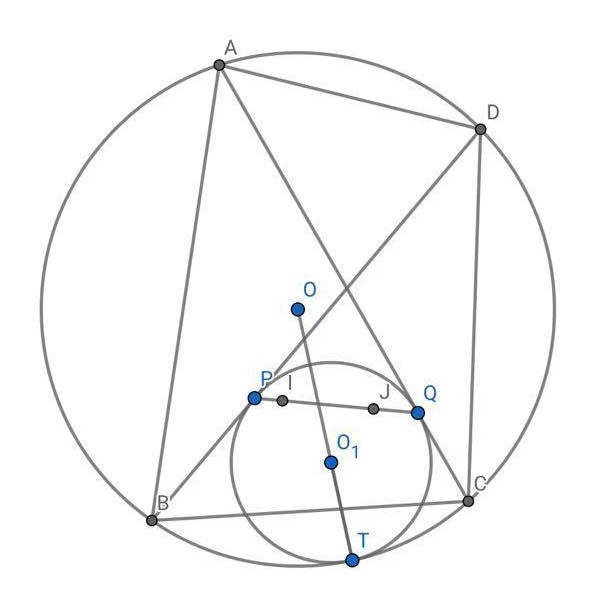
证明：位似倒角即可

牛顿定理

圆外切四边形对角线交点和以切点为顶点的四边形的对角线交点重合

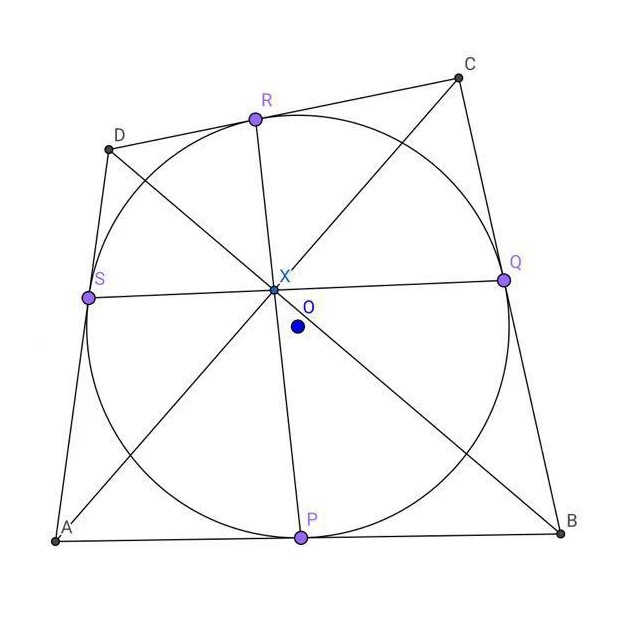
证明：同一法算比例易证

2.19更新

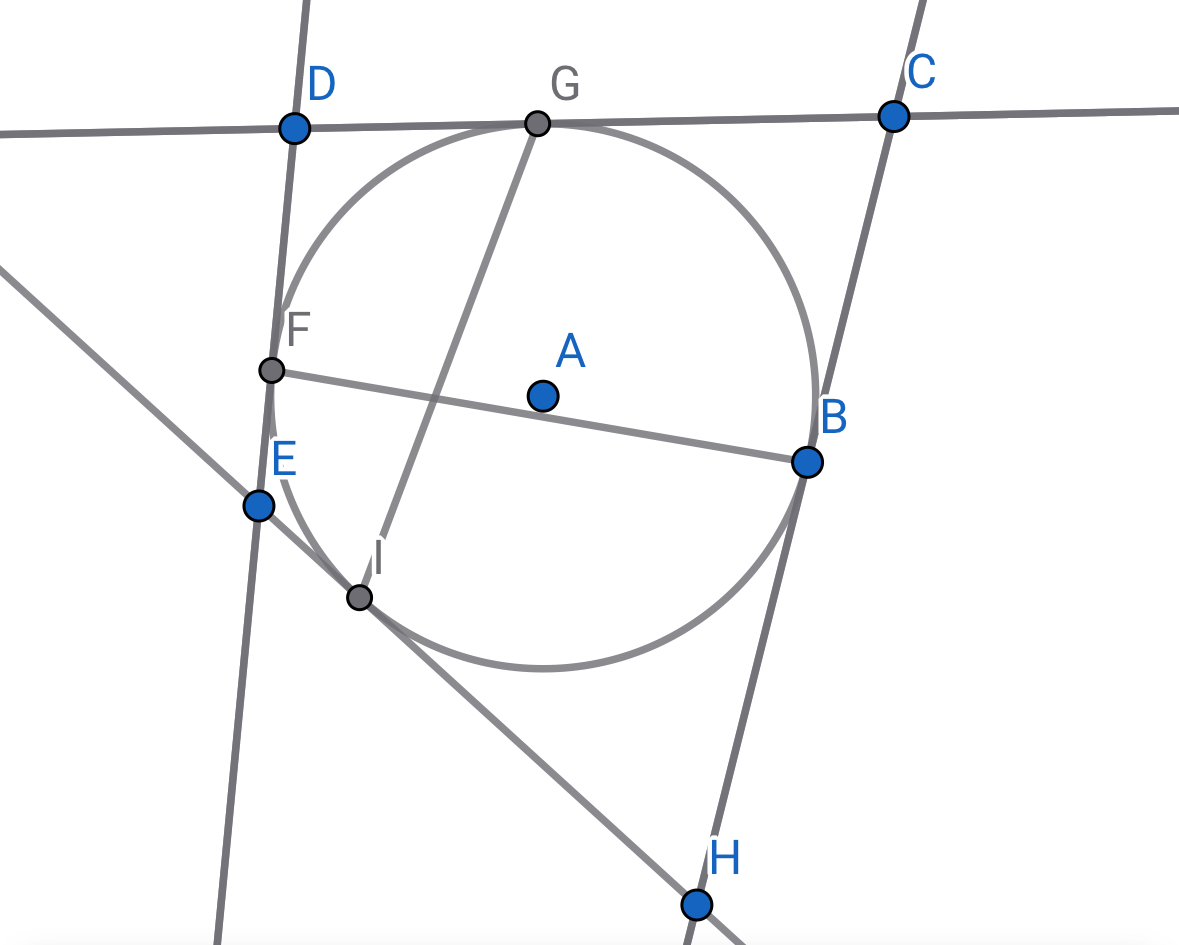
布列安桑定理

若一个六边形的六条边与一个圆相切，则它的三条相对定点连线共点

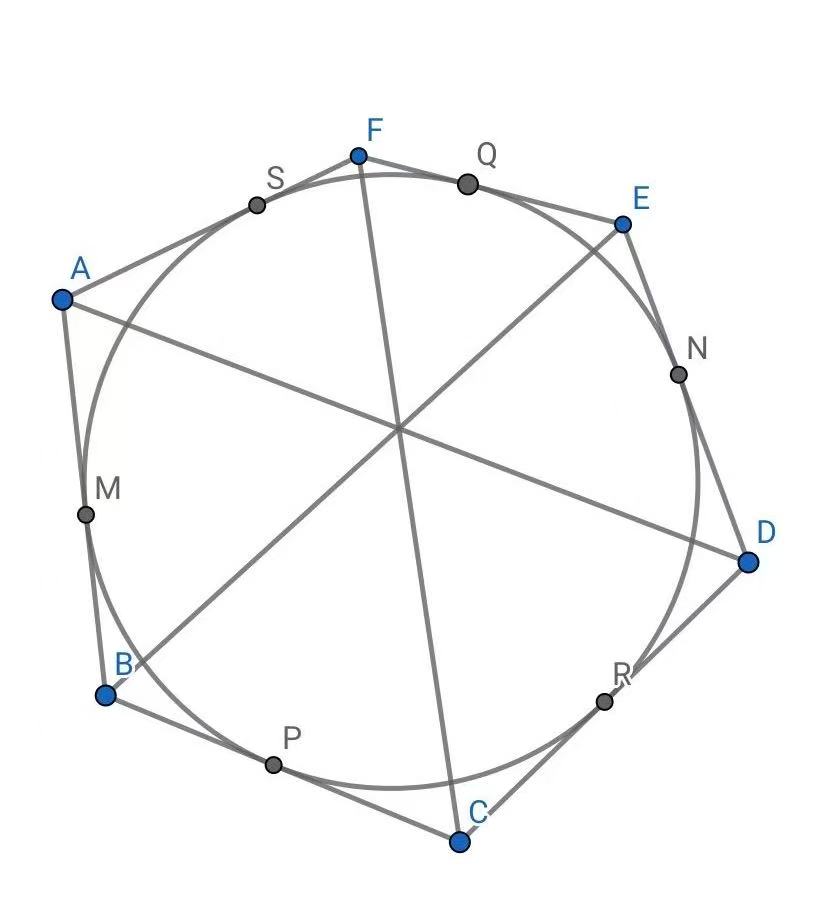
证明：如下图所示连接辅助线

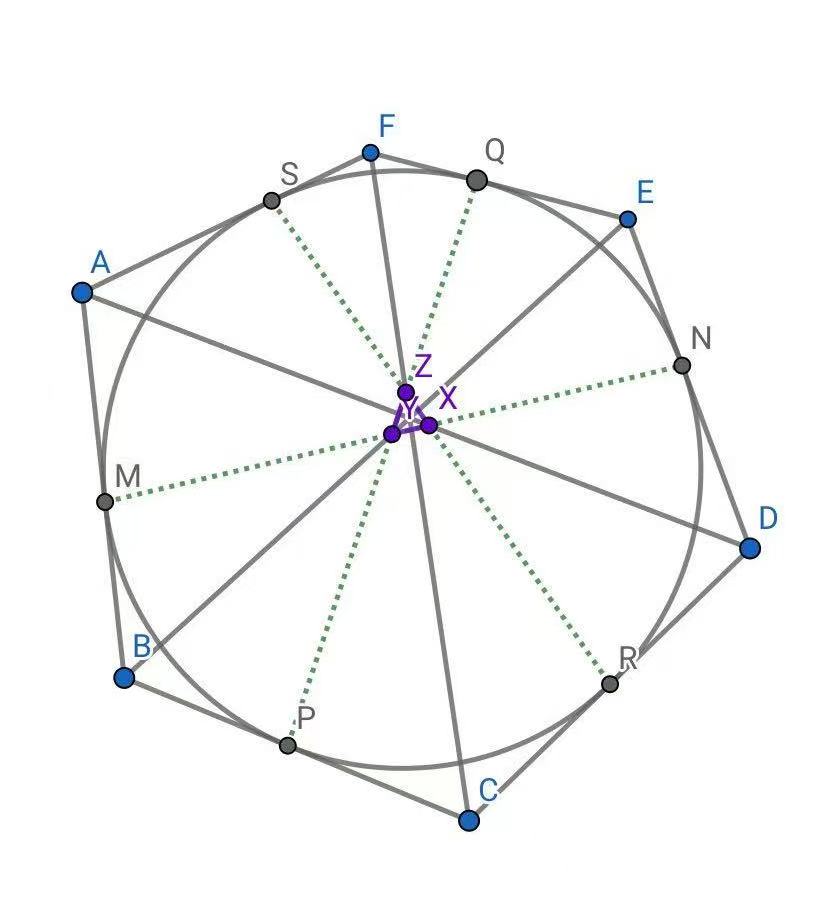
由牛顿定理，有$AD$、$RS$、$MN$共点，记为$X$

同理，$BE$、$MN$、$PQ$共点于$Y$，$CF$、$PQ$、$RS$共点于$Z$

若$X$、$Y$、$Z$中任意两点重合，则$X$、$Y$、$Z$重合，且$AD$、$BE$、$CF$共点于该重合点

若$X$、$Y$、$Z$构成三角形

则$AD$、$BE$、$CF$共点

$\Leftrightarrow \frac{\sin ∠AXS}{\sin ∠AXM}=1$         注：这里在$\triangle XYZ$中使用了角元$Ceva$定理

$\Leftrightarrow \frac{AS\sin ∠ASX}{AX}{\div}\frac{AM\sin ∠AMX }{AX}=1$

$\Leftrightarrow \frac{\sin ∠ASX}{\sin ∠AMX}=1$

由弦切角定理知成立，证毕

3.1更新

布洛卡（$Brocard$）点

已知三角形$ABC$，$P$是内部一点，若$∠PAB=∠PBC=∠PCA=\alpha$，则$P$为布洛卡点，$\alpha$为布洛卡角

有且仅有一点$P'$满足$∠P'BA=∠P'CB=∠P'AC$，则$P'$也是三角形的布洛卡点

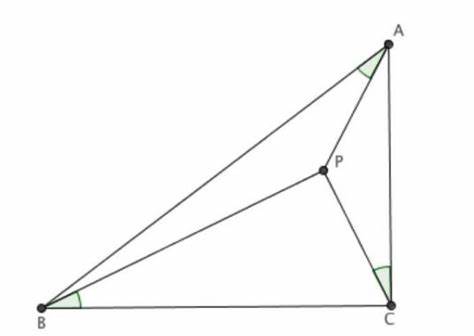
对布洛卡角$\alpha$，有以下结论

$\cot \alpha =\cot A + \cot B + \cot C = \frac{a^2+b^2+c^2}{4S} $

$\frac{1}{\sin^2 \alpha} = \frac{1}{\sin^2A}+\frac{1}{\sin^2B}+\frac{1}{\sin^2C}$

3.16更新

笛沙格定理

$ \triangle ABC$与$ \triangle A'B'C'$中，$BC$与$B'C'$，$CA$与$C'A'$，$AB$与$A'B'$的交点分别为$X$、$Y$、$Z$.若$AA'$、$BB'$、$CC'$共点于$O$，则$X$、$Y$、$Z$共线；反之，若$X$、$Y$、$Z$共线，则$AA'$、$BB'$、$CC'$共点于$O$或互相平行.

证明：

进行射影变换，将 $AB\bigcap XY$ 与 $BC\bigcap YZ$ 映射至无穷远点.

则两个条件均等价于 $ \triangle ABC$ 与 $ \triangle XYZ$ 位似.    证毕.

3.31更新

托勒密定理：对于一个内接圆的四边形，四边形的对角线乘积等于两组对边乘积之和.

推广：对任意凸四边形，四边形的对角线乘积大于等于两组对边乘积之和，取等当且仅当四边形为圆内接四边形时。

（我们只证推广形式，即$AB\times CD+AD\times BC\ge AC\times BD$）

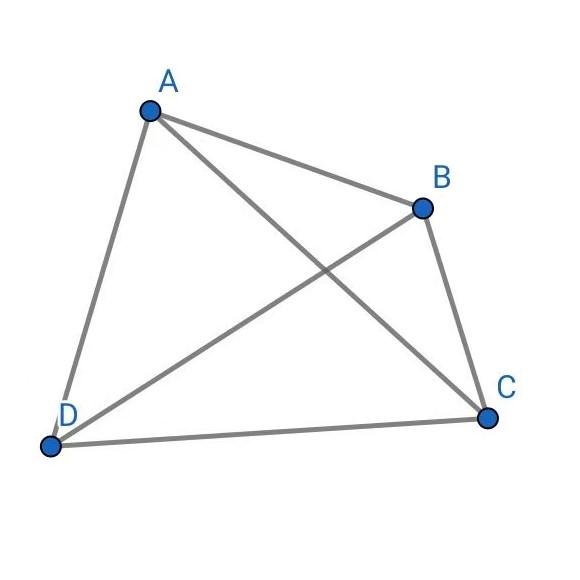
证明：以$A$为圆心，1为半径作反演变换

设$B$、$C$、$D$分别反演为$B'$ 、$C'$、$D'$

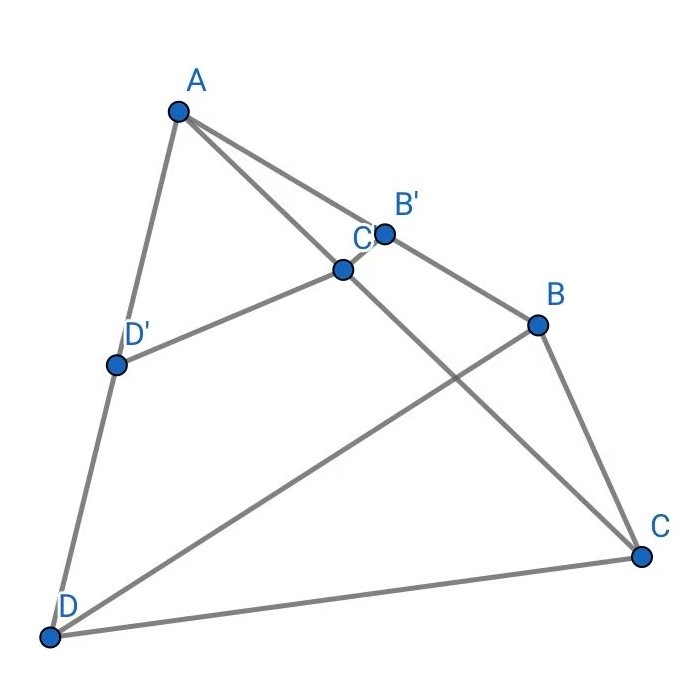
由$C'D'=\frac{1}{AD\times AC} \times CD$

   $B'C'=\frac{1}{AB\times AC} \times BC$

   $B'D'=\frac{1}{AB\times AD} \times BD$

及$C'D'+B'C'\ge B'D'$

即得$AB\times CD+AD\times BC\ge AC\times BD$

当且仅当$B'$ 、$C'$、$D'$共线，即$A$、$B$、$C$、$D$共圆时，等号成立

4.11更新

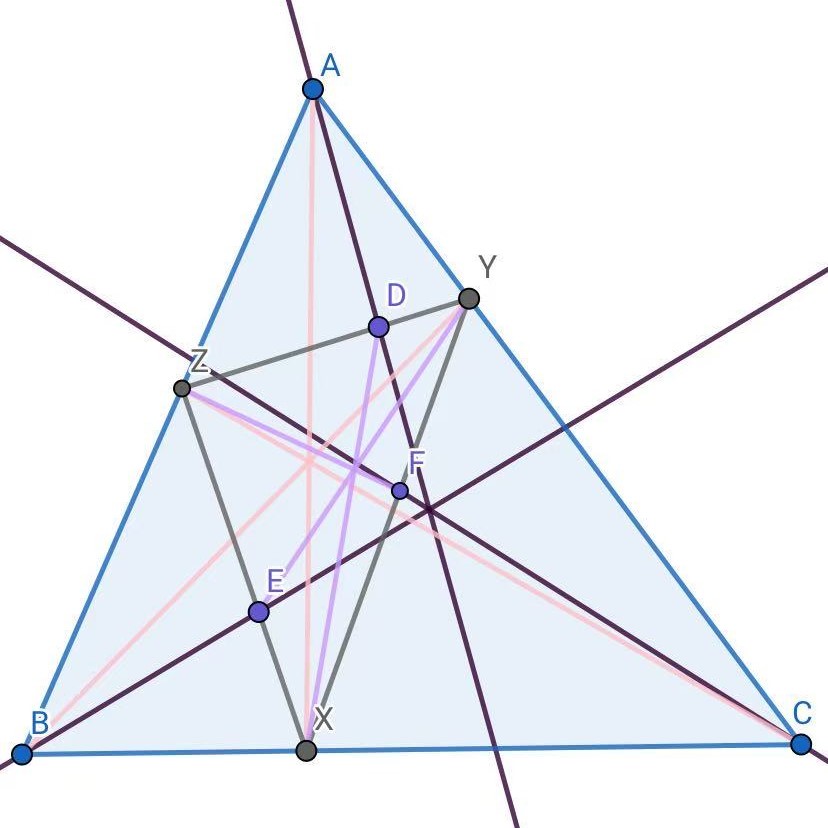
嵌套塞瓦定理

如图，设$AX$、$BY$、$CZ$共点，$XD$、$YE$、$ZF$共点，则$AD$、$BE$、$CF$共点.