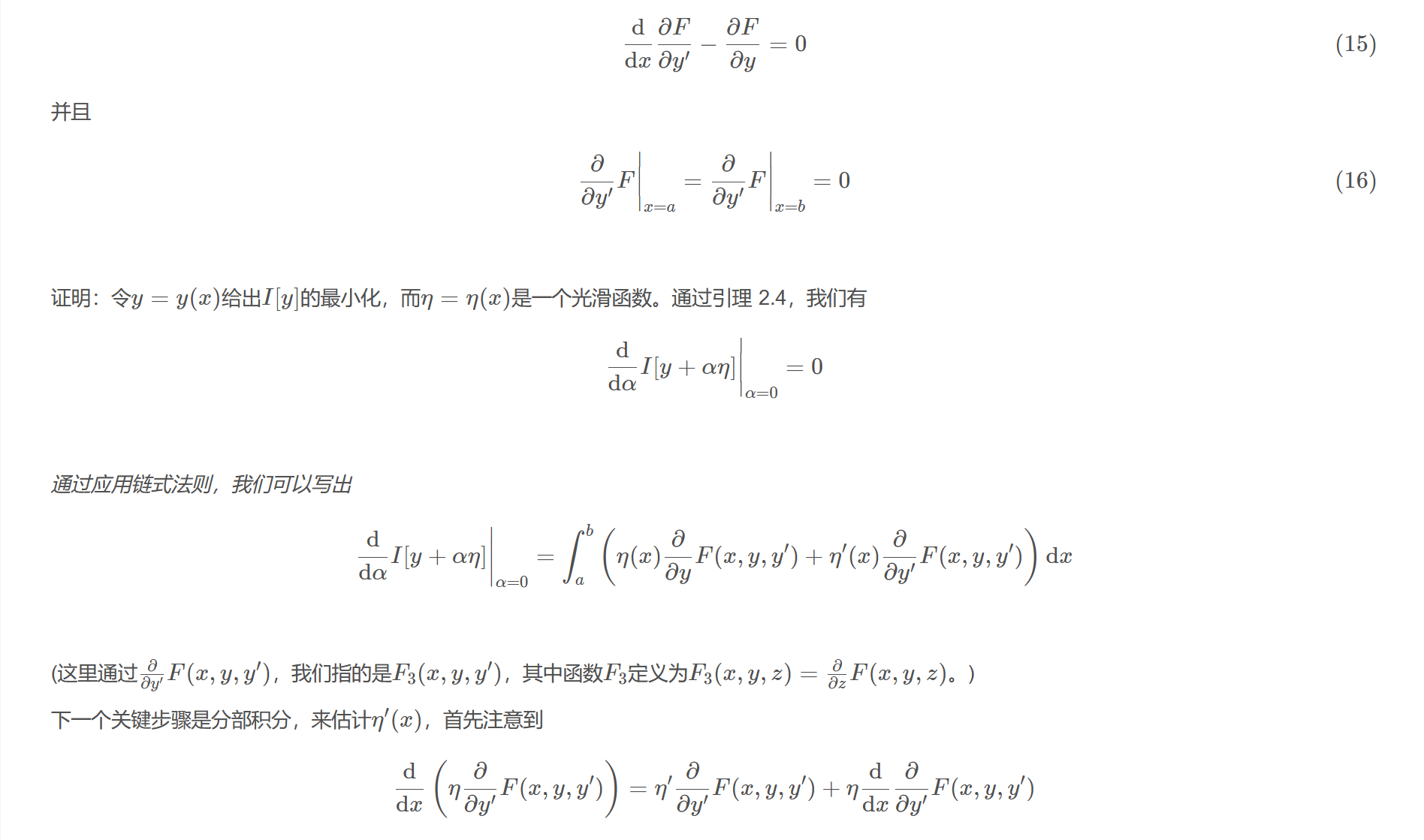§2 Euler-Lagrange方程

我们现在来一般地考虑寻找$y(x)$给出泛函$$I[y]=\int_{a}^{b}F(x,y(x),y^{\prime}(x))\mathrm{d}x\tag{8}$$稳定值。

我们在微分方程1中证明Picard定理时，有时将$F$视为$x, u, v$这三个独立变量的函数，有时则通过将$u = y(x)$和$v = y^{\prime}(x)$代入，只把它当作$x$的函数。例如，链式法则给出：$$\begin{aligned}\frac{\mathrm{d}}{\mathrm{d} x} F(x, y(x), y^{\prime}(x)) &= \frac{\partial F}{\partial x} + \frac{\partial F}{\partial y} \frac{\mathrm{d} y}{\mathrm{d} x} + \frac{\partial F}{\partial y^{\prime}} \frac{\mathrm{d}^2 y}{\mathrm{d} x^2}\\ &= \frac{\partial F}{\partial x} + y^{\prime} \frac{\partial F}{\partial y} + y^{\prime \prime} \frac{\partial F}{\partial y^{\prime}},\tag{9}\end{aligned}$$其中$\frac{\partial F}{\partial y^{\prime}}$表示$F(x, u, v)$对其第三个变量$v$的偏导数，并在$u = y(x)$和$v = y^{\prime}(x)$处取值。

从一个完整严格的观点来看，我们需要确定函数$y(x)$的确切的类使得泛函取得稳定值(可微，连续导数可微，可微到任意阶？)，且我们需要一些概念说明什么是在改变一个函数到一个‘附近’函数，通过把一个度规或至少一个拓扑“放”在函数的类上。

本文中我们假设所有的函数对于要处理的问题都是足够可微的。我们通常表述成光滑(无穷可微)函数的结果，因为现实世界中的大多数情况都是光滑的(或者可以被光滑函数任意地逼近)。为了这一点的合理性，我们将使用‘bump函数’。

引理 2.1 (bump函数) 存在一个函数$B(x)$具有下面的性质：(1) $B(x)$是无穷可微，(2) $B(x)=0$除非$x\in[0,1]$，(3) $0<B(x)\leqslant 1$如果$x\in(0,1)$。

证明：令$B(x)$是函数

$$B(x)=\left\{\begin{aligned}&0, & x\leqslant 0,\\&\exp(-x^{-1}(1-x)^{-1}), & 0<x<1,\\&0,&x\geqslant 1.\end{aligned}\right.$$

则对于所有$n$，当$x\downarrow0$或$x\uparrow 1$时$B^{(n)}(x)\to 0$(因为指数衰减占据了多项式增长的主导)，所以$f$在$0$或$1$处无穷可微，所以到处都无穷可微。很明显，$0\leqslant B(x)\leqslant 1$并且当且仅当$x\in(0,1)$时，$B(x)>0$。$$~\tag*{$\square$}$$

通过考虑$B((x-a)/(b-a))$，我们可以在任意区间$[a,b]$上定义‘bump函数’，并且通过缩放，我们可以假设它在中点取值为$1$(在它的最大处)，这在有的时候会很方便。

因此，一个函数总是可以在任何区间内变化（通过增加一个bump函数）而不影响其可微性，而且我们谈论的可微性的程度并不重要。

引理 2.2 (检验函数引理I) 令$y(x)$是$[a,b]$上一个连续函数，使得$$\int_{a}^{b}y(x)\eta(x)\mathrm{d}x=0\tag{10}$$对于任意光滑函数$\eta(x)$有$\eta(a)=\eta(b)=0$。则对于$x\in[a,b]$，$y(x)=0$。

证明：用反证法证明，假设对于一些$x_{0}\in(a,b)$，$y(x_{0})\neq 0$。不失一般性地假设$y(x_{0})>0$。则我们在某些包含$x_{0}$的区间$[c,d]$（其中$a<c<d<b$）上必须有$y(x)>0$。(因为$y(x)$是连续的。)现在在$[c,d]$上选取一个bump函数$b(x)$。通过假设$$\int_{a}^{b}y(x)b(x)\mathrm{d}x=0,$$但是因为$b(x)=0$除非$x\in[c,d]$，这意味着$$\int_{c}^{d}y(x)b(x)\mathrm{d}x=0,$$这是不可能的，因为$y(x)b(x)$是正的且在这个区间是连续的。与前提假设相矛盾，因此我们在$[a,b]$上必须有$y(x)=0$。$$~\tag*{$\square$}$$

这个定理的一个小变化如下。

引理 2.3 (检验函数引理II) 令$y(x)$是$[a,b]$上的连续函数，$c_{1},c_{2}$是常数，使得：对于任意光滑函数$\eta(x)$，有$$c_{1}\eta(a)+c_{2}\eta(b)+\int_{a}^{b}y(x)\eta(x)\mathrm{d}x=0\tag{11}$$则对于$x\in[a,b]$，有$c_{1}=c_{2}=0$和$y(x)=0$。

证明：先假设$c_{1}\neq 0$，那么不失一般性地假设$c_{1}>0$。令$\eta(x)$是区间$[a-\epsilon,a+\epsilon]$上的一个bump函数，所以$\eta(a)=1$,对于$x>a+\epsilon$,$\eta(x)=0$,并且$\eta(x)\in[0,1]$。我们看到对于$\epsilon$足够小，有$$0=c_{1}\eta(a)+c_{2}\eta(b)+\int_{a}^{b}y(x)\eta(x)\mathrm{d}x\geqslant c_{1}-\int_{0}^{a+\epsilon}|y(x)|\mathrm{d}x>0$$这出现矛盾了。因此我们必须有$c_{1}=0$。相同的讨论得出$c_{2}=0$。则通过引理 2.2，我们有$y(x)=0$，给出了结论。$$~\tag*{$\square$}$$

我们现在开始分析泛函$I[y]$的稳定值。我们可能很想尝试用某个无穷小函数$\delta(x)$来改变$I[y]$，但有无数个可能的函数，这会导致很多困难。为了避免担心这些可能性，我们转而关注某个单个一维变分系列。我们固定一个函数$\eta(x)$，并考虑$$y(x)+\alpha\eta(x)\tag{12}$$其中，$\alpha$是一个实参数。这允许我们来考虑$$I[y+\alpha\eta]=\int_{a}^{b}F(x,y+\alpha\eta,y^{\prime}+\alpha\eta^{\prime})\mathrm{d}x\tag{13}$$特别的我们有下面的引理。

引理 2.4 (最小值给出稳定值) 令$y(x)$给出$I[y]$的最小值，而$\eta(x)$是一个光滑函数。则我们有$$\left.\frac{\mathrm{d}}{\mathrm{d}\alpha}I[y+\alpha\eta]\right|_{\alpha=0}\tag{14}$$证明：这实际上只是标准的微积分极小值判据的另一种表现形式。如果$y(x)$给出$I$的最小值，则对于所有在零的邻域中的$\alpha$有$I[y+\alpha\eta]\geqslant I[y]$，所以$f(\alpha)=I[y+\alpha \eta]$在$\alpha=0$时取得最小。因此$f^{\prime}(0)=0$，这正是引理的表述。$$~\tag*{$\square$}$$

引理 2.5 (约束最小值给出稳定值) 令$y(x)$给出$I[y]$的最小值，受制于$y(a)=c_{1}$和$y(b)=c_{2}$，而$\eta(x)$是一个光滑函数且$\eta(a)=\eta(b)=0$。则我们有

$$\dfrac{\mathrm{d}}{\mathrm{d}\alpha} I[y+\alpha\eta]\bigg|_{\alpha=0}=0$$

证明：和之前的证明一样，注意到如果$\eta(a)=\eta(b)=0$，则$y+\alpha\eta$仍然满足约束$y(a)=c_{1}$和$y(b)=c_{2}$。

$$~\tag*{$\square$}$$

定理 2.6 (自然边界条件的Euler-Lagrange方程) 令$I[y]$是泛函$$I[y]:=\int_{a}^{b}F(x,y,y^{\prime})\mathrm{d}x$$对于一些光滑函数$F$。则$y(x)$给出$I$的最小化满足$$\frac{\mathrm{d}}{\mathrm{d}x}\frac{\partial F}{\partial y^{\prime}}-\frac{\partial F}{\partial y}=0\tag{15}$$并且

$$\dfrac{\partial}{\partial y^{\prime}}F\bigg|_{x=a}=\dfrac{\partial}{\partial y^{\prime}}F\bigg|_{x=b}=0\tag{16}$$

证明：令$y=y(x)$给出$I[y]$的最小化，而$\eta=\eta(x)$是一个光滑函数。通过引理 2.4，我们有

$$\dfrac{\mathrm{d}}{\mathrm{d}\alpha}I[y+\alpha\eta]\bigg|_{\alpha=0}=0$$

通过应用链式法则，我们可以写出

$$\dfrac{\mathrm{d}}{\mathrm{d}\alpha}I[y+\alpha\eta]\bigg|_{\alpha=0}=\int_{a}^{b}\left(\eta(x)\dfrac{\partial}{\partial y}F(x,y,y^{\prime})+\eta^{\prime}(x)\dfrac{\partial}{\partial y^{\prime}}F(x,y,y^{\prime})\right)\mathrm{d}x$$

(这里通过$\frac{\partial}{\partial y^{\prime}}F(x,y,y^{\prime})$，我们指的是$F_{3}(x,y,y^{\prime})$，其中函数$F_{3}$定义为$F_{3}(x,y,z)=\frac{\partial}{\partial z}F(x,y,z)$。)

下一个关键步骤是分部积分，来估计$\eta^{\prime}(x)$，首先注意到$$\frac{\mathrm{d}}{\mathrm{d}x}\left(\eta\frac{\partial}{\partial y^{\prime}}F(x,y,y^{\prime})\right)=\eta^{\prime}\frac{\partial}{\partial y^{\prime}}F(x,y,y^{\prime})+\eta\frac{\mathrm{d}}{\mathrm{d}x}\frac{\partial}{\partial y^{\prime}}F(x,y,y^{\prime})$$所以

$$\int_{a}^{b}\eta^{\prime}(x)\dfrac{\partial}{\partial y^{\prime}}F(x,y,y^{\prime})\mathrm{d}x=\left[\eta\dfrac{\partial}{\partial y^{\prime}}F(x,y,y^{\prime})\right]_{a}^{b}-\int_{a}^{b}\eta(x)\dfrac{\mathrm{d}}{\mathrm{d}x}\dfrac{\partial}{\partial y^{\prime}}F(x,y,y^{\prime})\mathrm{d}x$$

(这里$\frac{\mathrm{d}}{\mathrm{d}x}$表示全导数，作用在显式或非显式出现的$x$上($y$和$y^{\prime}$中)。)

因此

$$\frac{\mathrm{d}}{\mathrm{d}\alpha}I[y+\alpha\eta]\bigg|_{\alpha=0}=\left[\eta\dfrac{\partial F}{\partial y^{\prime}}\right]_{a}^{b}+\int_{a}^{b}\eta(x)\left(\dfrac{\partial F}{\partial y}-\frac{\mathrm{d}}{\mathrm{d}x}\frac{\partial F}{\partial y^{\prime}}\right)\mathrm{d}x$$

现在，为了$y$取得极值，方程等号左边在$\eta$的任意选取下必须消失。因此方程等号右边对于任意$\eta(x)$必须消失。但是对于引理 2.3意味着

$$\frac{\mathrm{d}}{\mathrm{d}x}\frac{\partial F}{\partial y^{\prime}}-\frac{\partial F}{\partial y}=0$$

和

$$\dfrac{\partial}{\partial y^{\prime}}F\bigg|_{x=a}=\dfrac{\partial}{\partial y^{\prime}}F\bigg|_{x=b}=0$$

如要求的一样。

$$~\tag*{$\square$}$$

定理 2.7 (固定端点边界条件Euler-Lagrange方程) 令$I[y]$是泛函$$I[y]:=\int_{a}^{b}F(x,y,y^{\prime})\mathrm{d}x$$对于一些光滑函数$F$。则$y(x)$给出$I$的最小值和$y(a)=c_{1}$与$y(b)=c_{2}$满足$$\frac{\mathrm{d}}{\mathrm{d}x}\frac{\partial F}{\partial y^{\prime}}-\frac{\partial F}{\partial y}=0\tag{17}$$证明：这与前面的证明基本相同，通过引理 2.5，我们只考虑函数$\eta$满足$\eta(a)=\eta(b)=0$。对于所有这样的函数，我们发现

$$\begin{aligned}0=\dfrac{\mathrm{d}}{\mathrm{d}\alpha}I[y+\alpha\eta]\bigg|_{\alpha=0}&=\left[\eta\dfrac{\partial F}{\partial y^{\prime}}\right]_{a}^{b}+\int_{a}^{b}\eta(x)\left(\dfrac{\partial F}{\partial y}-\dfrac{\mathrm{d}}{\mathrm{d}x}\dfrac{\partial F}{\partial y^{\prime}}\right)\mathrm{d}x\\&=\int_{a}^{b}\eta(x)\left(\dfrac{\partial F}{\partial y}-\dfrac{\mathrm{d}}{\mathrm{d}x}\dfrac{\partial F}{\partial y^{\prime}}\right)\mathrm{d}x\end{aligned}$$

(项$\left[\eta\frac{\partial F}{\partial y^{\prime}}\right]_{a}^{b}$消失，因为$\eta(a)=\eta(b)=0$。)现在根据引理 2.2，我们看到我们必须有

$$\frac{\mathrm{d}}{\mathrm{d}x}\frac{\partial F}{\partial y^{\prime}}-\frac{\partial F}{\partial y}=0$$

如要求的一样。

$$~\tag*{$\square$}$$

注意：找到极值和稳定值与找到最大值或最小值并不是一回事。它需要一些进一步的信息来确定一个极值是（局部）最大值，还是（局部）最小值，或者两者都不是。然而，最大值和最小值必须是极值。