数学

[代数专题]因式分解技巧补充——轮换式与对称式

[2025年6月5日已更新]                       备注：本人是在@棋虫因式分解帖子作出补充

你是一名刚踏入数学竞赛旅途的初中生，对竞赛中的奇异景象充满好奇和憧憬。然而事实上并没有那么简单，你遇到了第一座大山：因式分解

一天晚上，你一人在教室里刷因式分解的题型，因式分解原本是你的拿手好戏，基本都是口答，可是现如今你却在一道题中踌躇不决

$(y-z)^5+(z-x)^5+(x-y)^5$

你内心瞬间怀疑人生，这样的五次多项式怎么可能被因式分解呢？

这时教室门突然响了一下，一位身着黑布衫的女孩走进教室来，原来是全班公认的学霸——张浩宇

“我来拿点书，这么晚了还不回去啊？”她面带微笑望着你

“没有......我在想一道题”不知道为什么，你一跟女生说话就紧张

“让我看看，”张浩宇拿起题目仔细端详了一下，“如果你学过轮换式与对称式，那么这道题会很简单。你最近在学竞赛吗？”

“没有，只是了解一下，对了能跟我详细讲一讲吗？”

“当然可以！”她兴致勃勃地在草稿本上工整地写下几个式子：

$x+y$，$xy$，$x^2+y^2$，$x^3+y^3$，$x^2y+xy^2$...

“这些式子在数学中极其常见，尤其是在乘法公式中无处不在。那么，现在请你将x和y互相交换，告诉我会发生什么现象？”

你在每式下方进行交换，发现一个奇异的现象：交换后的式子竟然和原式一模一样！

   “看来你已经发现啦，没错，像上面这样的式子，在字母x和y任意互换位置时，保持不变，我们就称为x，y的对称式”

此时我内心积攒的无数问题都爆发了:“如果说有3个字母，就比如说是关于x，y，z的呢？”

“那就是x，y，z中任意两个字母互换位置，保持不变，就称为x，y，z的对称式，以下类比即可。”张浩宇云淡风轻道

“原来是这样，”我对眼前这些式子又有了新的看法，“有一说一，这和几何中的对称有着异曲同工之妙呢”

“没错！”张浩宇忽然站起身，仰望漫天繁星，“这大抵是独属于数学的美吧”

望了望张浩宇，心里似乎明白了什么...

“好啦，时间不早啦！关于轮换式以及利用他们因式分解明天再讲吧！”张浩宇回到座位上清理好自己所要的书📖，“数学是一门很有趣的学科，值得我们去深究”

你目送着她离开，望着她的背影，又多出了一丝敬意(但是她那句话我不敢苟同🤫)

转眼就到了第二天大课间。

“事不宜迟，我们现在就来聊聊轮换式吧，轮换式其实和对称式是有相似之处的，但是呢比它更加一般化,”张浩宇边说边在纸上写着，“所谓轮换，讲究的是一一对应，我们以xy+yz+xz为例，将x换为y，将y换为z，将z换成x，我们便会惊奇的发现”

“和原来完全一样”你略带惊讶地回答道

“没错，和原来一致，”张浩宇停了停笔，淡淡喝了一口水，“我们就称xy+yz+xz为x，y，z的轮换式，类似地还有xyz。他们之间有一些微妙的关系，可是这些微妙的关系并不足以支撑对称性，这也是轮换式名字由来”

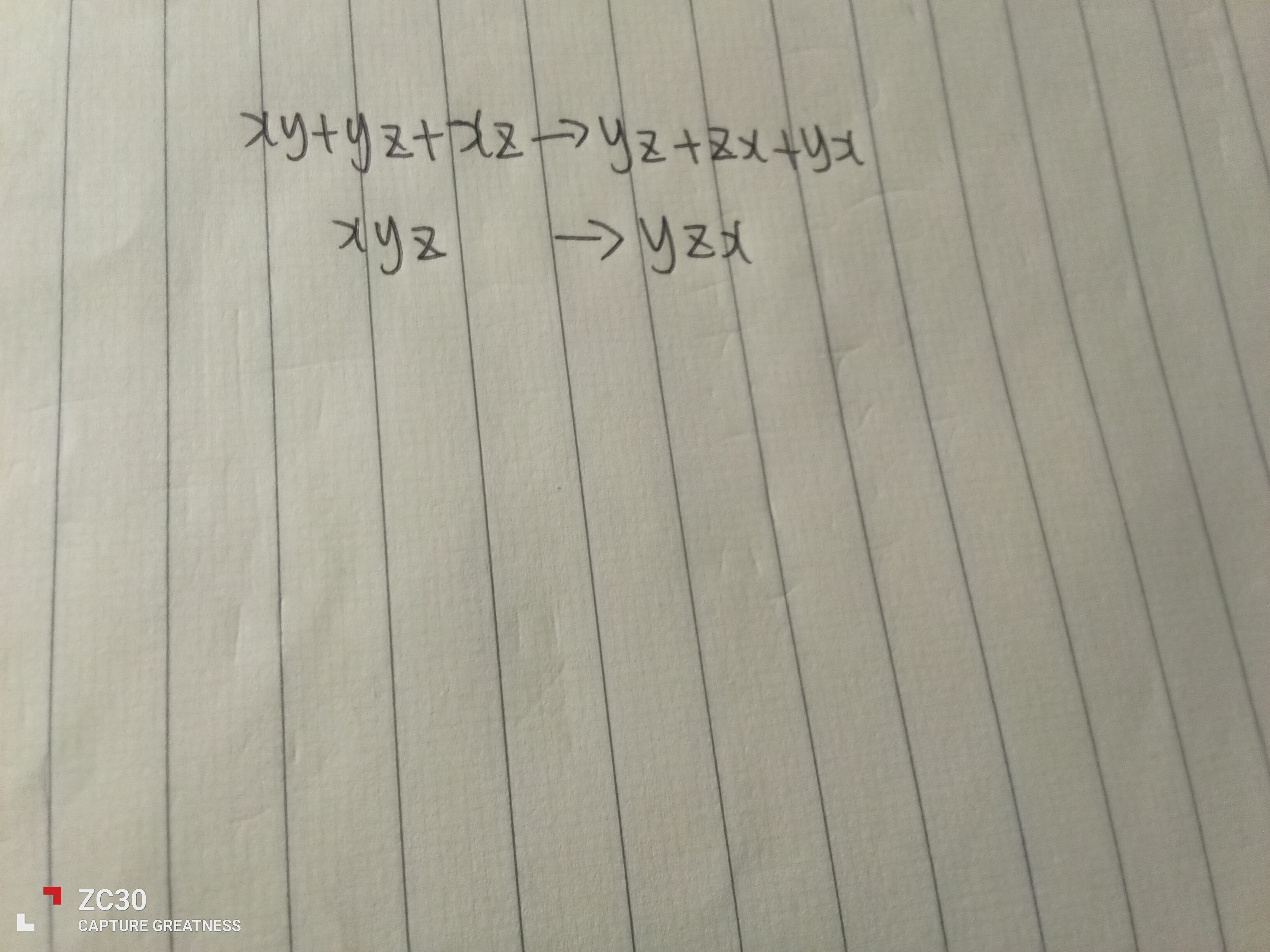
此时你瞬间恍然大悟：“那这么说，轮换式与对称式是包含关系咯！”

“不错嘛，都会自己总结了！没错,他们就是包含关系，轮换式不一定是对称式，但是对称式一定是轮换式。你可以类比 正方形，长方形，平行四边形之间的关系。例如，$x^2y+y^2z+z^2x$是轮换式，但是如果任意交换两个字母，便会与原式不等，故而不是对称式了。用韦恩图表示就是这样”

“特别地，次数低于3的轮换式也是对称式”张浩宇在草稿本上奋笔疾书📖着。

“原来如此啊，我明白啦！”你脸上洋溢着兴奋和喜悦，“讲了一大堆理论，可以开始讲如何利用他们因式分解了吗？”

“当然不能啦，要想学习如何利用他们因式分解，首先得接受我的灵魂三问。”张浩宇故作神秘道

“哪三问？快说吧我都等不及了！”你内心充溢着对知识的渴望。

“№1.你会因式定理和待定系数法吗？”   “那必然是会的，@棋虫的帖子我都看了哦。 ”

“№2.你知道基本轮换式有哪些吗？”       “em...不太知道诶，能详细写出来吗？”   “好，你看好了哦，基本上因式分解结果都是由他们组成的”

“№3.你知道轮换式之间有什么关系吗？”    “似乎也不是很清楚啊，讲一讲吧。”   “好，那就请听好了！”

“我们现已知两个关于x，y，z的轮换式$x^2yz+xy^2z+xyz^2$和$xyz$，将他们进行加减乘除运算，告诉我会发生什么？”

我埋头在草稿本上运算，猛然间惊奇的发现——他们的结果竟然均为轮换式！！

 “看来你已经发现啦！”张浩宇一本正经道，“对于轮换式之间，他们之间进行加减乘除后仍是轮换式，值得一提的是，两个轮换式之间要为整除的关系才满足这个结论。”

张浩宇丝毫没有要停下的架势：“类比推理可知，对称式也满足这个结论，即加减乘除后仍是对称式，之间也要为整除的关系。也就是说，我们将对称式或轮换式任意组合，结果必为轮换式”

“同时我们可以注意到，这个结论反之也成立，我们都知道整式乘除的逆运算为因式分解”她喝了一口水，又振振有词道，“一个轮换式或者是对称式因式分解后结果一定是几个轮换式组成，前提是他一定能被因式分解，也验证了问题2所说，至于证明，举几个例子就明白了，我也写下几个例子。对了，特别地，齐次轮换式或齐次对称式四则运算结果也为齐次轮换式或对称式。”

你不禁感叹道：“原来小小的轮换式蕴藏着这么大的规律呢！真是神奇啊！”

“是啊，数学的魅力就是如此！让你有一种又爱又恨的感觉，捉摸不透”张浩宇又一次不自觉地仰望星空。望着她，我又一次心生敬意

叮铃铃～～～，上课了，你们连忙回到了自己的座位上。

时光如白驹过隙，很快就到了放学。张浩宇主动来到了你的座位💺旁。

“剩下的内容便留给如何利用他们因式分解和例题吧”张浩宇边准备草稿纸边讲道，“你觉得拿到题目前先要干啥？”

“先写解：和原式等于啦！”你条件反射般回答道，过了半天才反应过来，“e....应该要先读题”

“没错！”张浩宇和颜悦色道，“我们首先判断原式为几次齐次轮换式或几次齐次对称式”

“这样的目的是什么呢？”你又变成“十万个为什么”。

“你后面就知道啦！”张浩宇微微一笑，买下了一个关子，“其次，我们需要利用因式定理尝试试出原式的一个或几个有理根，不过值得一提的是，这里我们利用轮换式与对称式的性质，只需要试常见的轮换式即可，有的时候，我们试出来的因式经过轮换性质也可以得出另外的因式。别怪我没有提醒你，试根过程可能会极其困难，所以请保持耐心！”

张浩宇目不窥园，讲得格外的入迷：“接着，倘若因式定理不能再用时，我们要分析原式还缺几次因式，这个时候我们所判断的原式为几次轮换式就派上用场啦！假定原式为五次齐次轮换式，我们试出来的因式乘积为三次齐次轮换式，那么其余的因式必为二次齐次轮换式。请务必注意这是齐次，如果不齐次，就更麻烦了”

“然后，我们观察到，常见两次齐次轮换式只有$xy+yz+zx$和$x^2+y^2+z^2$，介于不知道他们的系数，我们便用待定系数法将他们的系数设出来”张浩宇在草稿纸上奋笔疾书

“最后，我们将这两个系数的值求出来，便可以完成因式分解，这里我分享两个求值方法。一是对比任意一项系数求值，二是赋值法，令字母值带入，切记一定不要使因式为0”

“额外补充一点🕐，如果说原式不为轮换式，且用一般方法无法做出，这时利用化归思想，使用恒等变形或换元法将其变为轮换式即可。”

“原来如此，实践出真知，可以用一道例题来具象你的方法吗？”你听得正入迷

“行，那我就以$a^3+b^3+c^3-3abc$为例，”张浩宇讲得面不改色，“首先观察可知原式为三次齐次轮换式。”

“其次，因式定理开用，这里一定要有耐心，之后我们便可以得出当$a=-b-c$时原式为$0$，则$a+b+c$为该原式的一个因式”

“接着，待定系数法开启，因为原式为三次齐次轮换式，试出的一个因式为一次齐次轮换式，所以另一个因式为二次齐次轮换式，我们便可以设仅有的两个常见的二次齐次轮换式的系数为l和m”

“然后，无论是对比系数还是赋值法均可，将l和m的值求出来”

“最后，代入参数，便可以得出因式分解最终的结果啦！”张浩宇一笔一画将过程写了出来

“相信你再看到那一道五次齐次轮换式，心里应该有了大致的思路吧！这道题就交给评论区的大佬们给你解答啦！”张浩宇语重心长道，

“到这里轮换式与对称式的内容就结束了，不过我们对他们的探索是永无止境的，它们不仅应用在因式分解中，而且在数学学习中的方方面面都有出处，这里既是终点，同时也是起点，让我们一起怀揣着对数学的热情，在数学的学习中越走越远！”

他入木三分的演讲令你热血沸腾：“好！让我们一起在数学旅途中共同成长，谢谢您这次的讲解！时间不早啦，下次再聊”

“好，下次再聊，有问题随时问我哦！”

望着张浩宇的背影，你不禁又心生敬意......

🌠知识补充：三个重要公式(注意到那个帖子并没有这个)

$①当n为奇数时，a^n+b^n=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}b^2-...-ab^{n-2}+b^{n-1})$

$②当n为偶数时，a^n-b^n=(a+b)(a^{n-1}-a^{n-2}b+a^{n-3}b^2-...+ab^{n-2}-b^{n-1})$

$②当n为正整数时，a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^2+...+ab^{n-2}+b^{n-1})$

✨例题引路

$求证：2^{1984}+1不是质数$

$证明：2^{1984}+1=2^{64×31}+1^{31}=(2^{64}+1)(2^{64×30}-2^{64×29}+...-2^{64}+1)$

$所以2^{64}+1是2^{1984}+1的真因数，它大于1，小于2^{1984}+1$

$所以2^{1984}+1不是质数$        证毕.