- 时间正序
- 时间倒序
- 评论最多
令$u=x^{n}$, 则$\mathrm{d}u=nx^{n-1}\mathrm{dx}$, 并且当$x=0$时, $u=0$, 当$x=1$时, $u=1$. 因此原积分变为
$$S=\int_{0}^{1}\sqrt[n]{1-x^{n}}=\int_{0}^{1}\sqrt[n]{1-u}\dfrac{1}{n}u^{\frac{1}{n}-1}\mathrm{d}u=\dfrac{1}{n}\int_{0}^{1}(1-u)^{\frac{1}{n}}u^{\frac{1}{n}-1}\mathrm{d}u$$
引入Beta函数
$$B(x,y)=\int_{0}^{1}t^{x-1}(1-t)^{y-1}\mathrm{d}t$$
则
$$S=\dfrac{1}{n} B\left(\dfrac{1}{n},\dfrac{n+1}{n}\right)$$
考虑Beta函数与Gamma函数的关系
$$B(x,y)=\dfrac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}$$
和Gamma函数的性质
$$\Gamma(z+1)=z\Gamma(z)$$
有
$$\begin{aligned}S&=\dfrac{1}{n}\dfrac{\Gamma\left(\dfrac{1}{n}\right)\Gamma\left(\dfrac{n+1}{n}\right)}{\Gamma\left(\dfrac{1}{n}+\dfrac{n+1}{n}\right)}\\&=\dfrac{1}{n}\dfrac{\Gamma\left(\dfrac{1}{n}\right)\Gamma\left(1+\dfrac{1}{n}\right)}{\Gamma\left(1+\dfrac{2}{n}\right)}\\&=\dfrac{1}{n}\dfrac{\Gamma\left(\dfrac{1}{n}\right)\dfrac{1}{n}\Gamma\left(\dfrac{1}{n}\right)}{\dfrac{2}{n}\Gamma\left(\dfrac{2}{n}\right)}\\&=\dfrac{1}{2n}\dfrac{\Gamma\left(\dfrac{1}{n}\right)^{2}}{\Gamma\left(\dfrac{2}{n}\right)}\end{aligned}$$
- 1

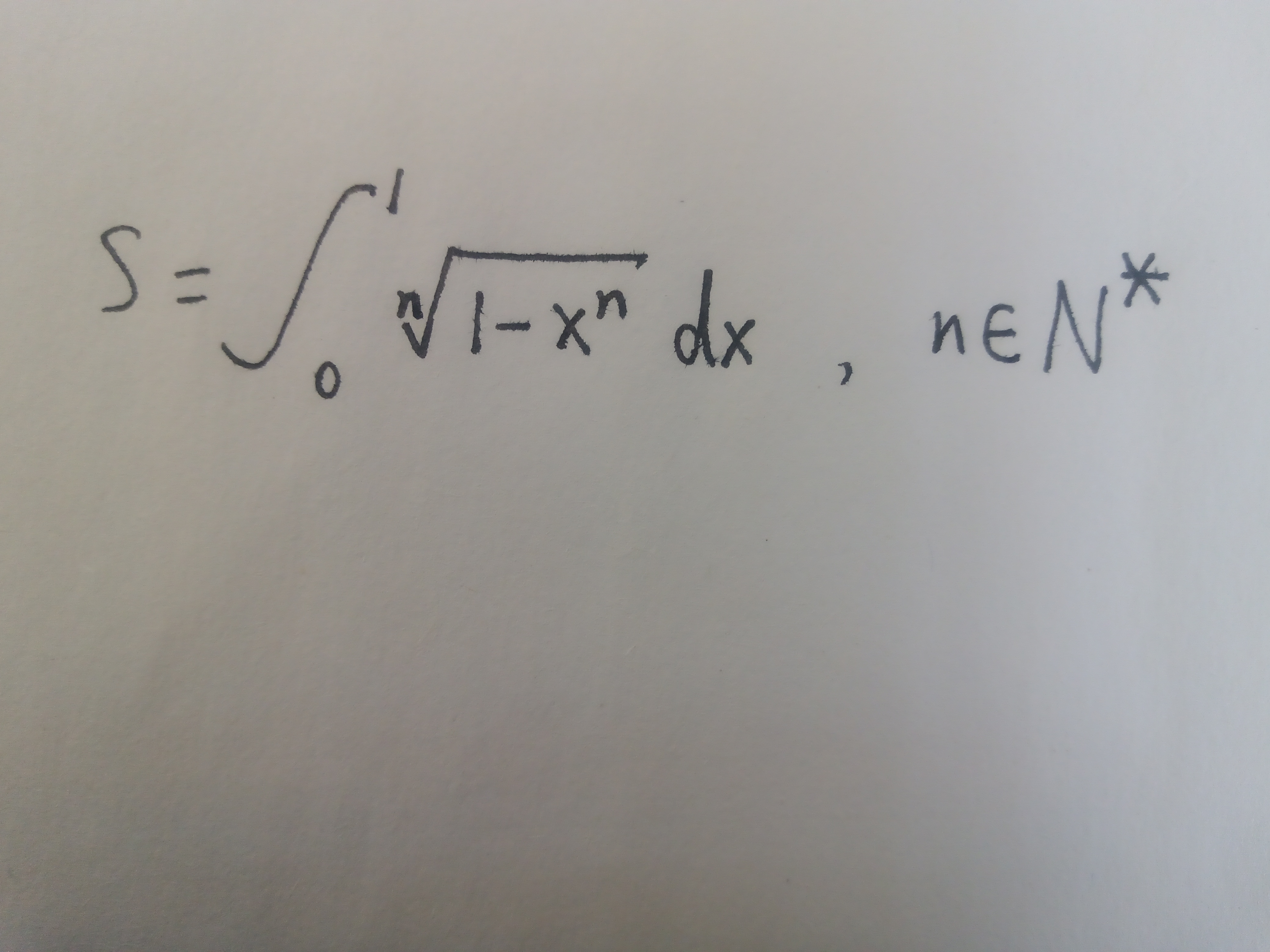 最后要把S写成关于n的函数(我不会用键盘打积分号,所以只好手写)
最后要把S写成关于n的函数(我不会用键盘打积分号,所以只好手写)