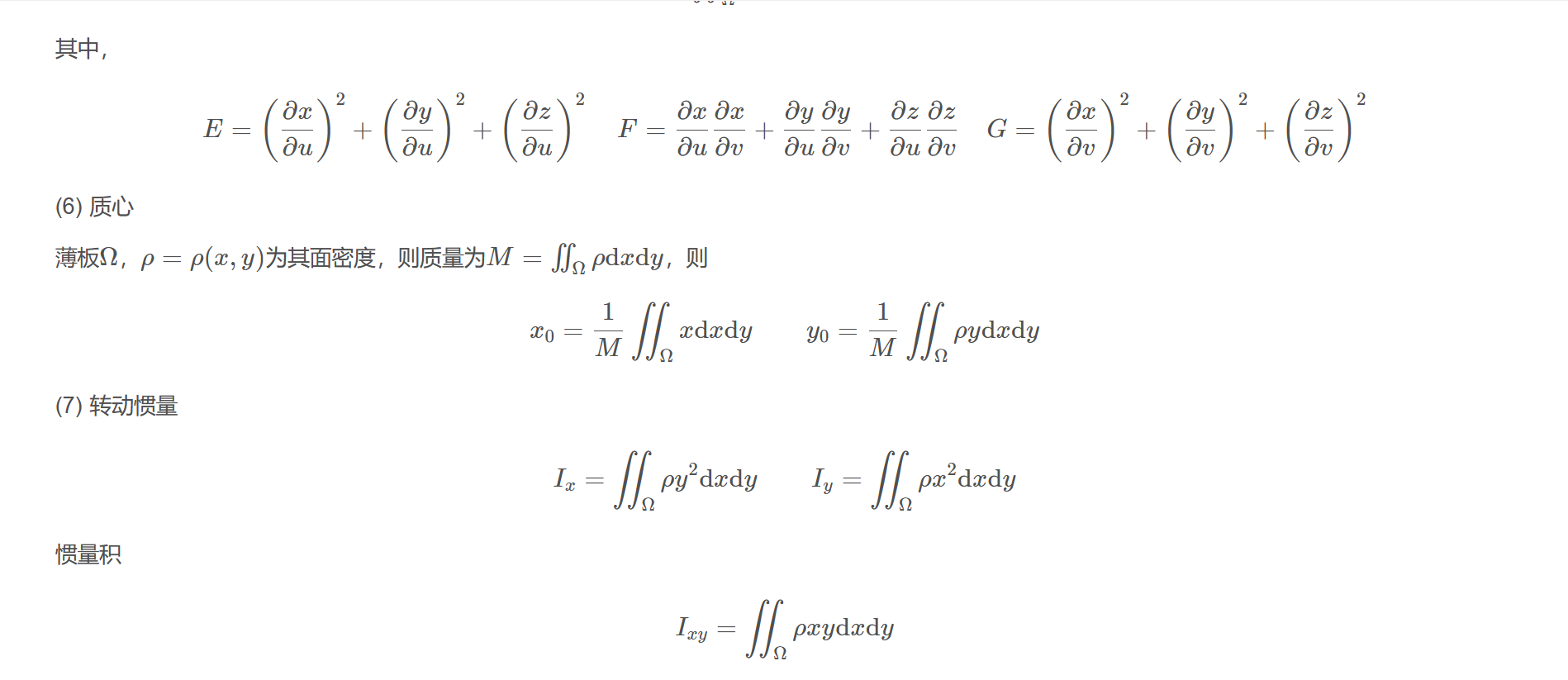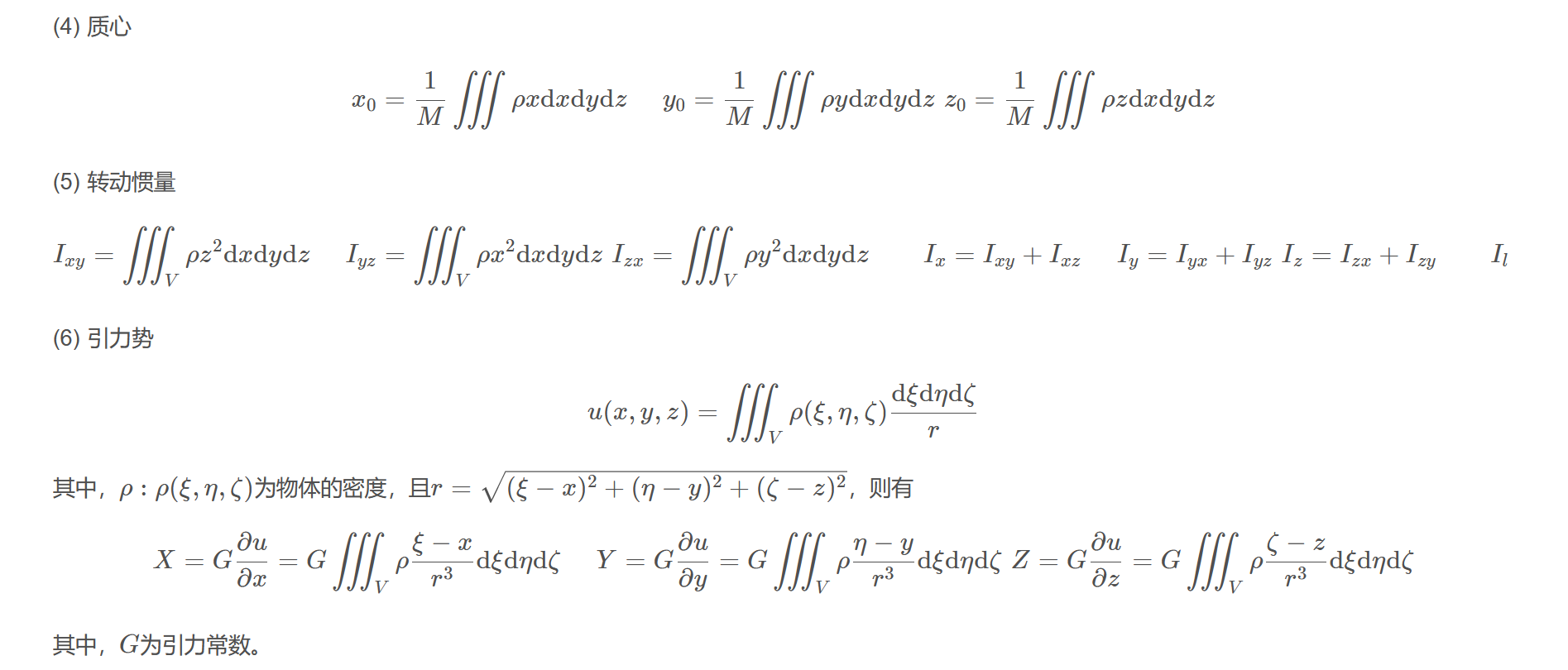二重积分

(1)$$\iint_{\Omega}f(x,y)\mathrm{d}x\mathrm{d}y=\lim\limits_{\substack{\max\left|\Delta x_{i}\right|\to 0\max\left|\Delta y_{i}\right|\to 0}}\sum_{i}\sum_{j}f(x_{i},y_{j})\Delta x_{i}\Delta y_{j},\quad\Delta x_{i}=x_{i+1}-x_{i}\quad\Delta y_{j}=y_{j+1}-y_{j},\quad (x_{i},y_{j})\in\Omega$$若区域$\Omega$由以下不等式给出：$$a\leqslant x\leqslant b\qquad y_{1}(x)\leqslant y\leqslant y_{2}(x)$$则有：$$\iint_{\Omega}f(x,y)\mathrm{d}x\mathrm{d}y=\int_{a}^{b}\mathrm{d}x\int_{y_{1}(x)}^{y_{2}(x)}f(x,y)\mathrm{d}y$$

(2) 若连续可微函数$x=x(u,v),y=y(u,v)$给出平面Oxy上的有限闭区域$\Omega$与平面Ouv上的区域$\Omega^{\prime}$之间一一映射，且$\frac{\partial(x,y)}{\partial(u,v)}$的符号在$\Omega$内保持不变(可能在零测度集上有例外)，则成立以下公式： $$\iint_{\Omega} f(x,y)\mathrm{d}x\mathrm{d}y=\iint_{\Omega^{\prime}}f\left[x(u,v),y(u,v)\right]\frac{\partial(x,y)}{\partial(u,v)}\mathrm{d}u\mathrm{d}v$$例如$$\iint_{\Omega}f(x,y)\mathrm{d}x\mathrm{d}y=\iint_{\Omega^{\prime}}f(r\cos\varphi,r\sin\varphi)r\mathrm{d}r\mathrm{d}\varphi$$

(3) 面积计算$$S=\iint_{S}\mathrm{d}x\mathrm{d}y=\iint_{S}r\mathrm{d}r\mathrm{d}\varphi$$

(4) 体积计算

设柱体顶面位于连续曲面$z=f(x,y)$，底面位于平面$z=0$，侧面垂直于底面，且底面在平面Oxy上所占区域$\Omega$是可求积的，则：柱体的体积$$V=\iint_{\Omega}f(x,y)\mathrm{d}x\mathrm{d}y$$

(5) 曲面面积的计算法

(a) 曲面由显函数给出的情况

光滑曲面$z=z(x,y)$的面积由以下积分表示$$S=\iint_{\Omega}\sqrt{1+\left(\frac{\partial z}{\partial x}\right)^{2}+\left(\frac{\partial z}{\partial y}\right)^{2}}\mathrm{d}x\mathrm{d}y$$其中，$\Omega$为该曲面在Oxy平面上的投影。

(b) 曲面由参数方程给出的情况

若曲面是由参数方程给出的$x=x(u,v),y=y(u,v),z=z(u,v)$，其中$(u,v)\in\Omega$，$\Omega$为封闭可求积的有限区域，且函数$x,y$和$z$在区域$\Omega$内连续可微，则对于曲面的面积有公式$$S=\iint_{\Omega}\sqrt{EG-F^{2}}\mathrm{d}u\mathrm{d}v$$其中，$$E=\left(\frac{\partial x}{\partial u}\right)^{2}+\left(\frac{\partial y}{\partial u}\right)^{2}+\left(\frac{\partial z}{\partial u}\right)^{2}\quad F=\frac{\partial x}{\partial u}\frac{\partial x}{\partial v}+\frac{\partial y}{\partial u}\frac{\partial y}{\partial v}+\frac{\partial z}{\partial u}\frac{\partial z}{\partial v}\quad G=\left(\frac{\partial x}{\partial v}\right)^{2}+\left(\frac{\partial y}{\partial v}\right)^{2}+\left(\frac{\partial z}{\partial v}\right)^{2}$$

(6) 质心

薄板$\Omega$，$\rho=\rho(x,y)$为其面密度，则质量为$M=\iint_{\Omega}\rho\mathrm{d}x\mathrm{d}y$，则$$x_{0}=\frac{1}{M}\iint_{\Omega}x\mathrm{d}x\mathrm{d}y\qquad y_{0}=\frac{1}{M}\iint_{\Omega}\rho y\mathrm{d}x\mathrm{d}y$$

(7) 转动惯量$$I_{x}=\iint_{\Omega}\rho y^{2}\mathrm{d}x\mathrm{d}y\qquad I_{y}=\iint_{\Omega}\rho x^{2}\mathrm{d}x\mathrm{d}y$$

惯量积$$I_{xy}=\iint_{\Omega}\rho xy\mathrm{d}x\mathrm{d}y$$

三重积分

(1) $x_{1}<x<x_{2},y_{1}(x)\leqslant y\leqslant y_{2}(x),z_{1}(x,y)\leqslant z\leqslant z_{2}(x,y)$，$f(x,y,z)$连续，$y_{1}(x),y_{2}(x),z_{1}(x,y),z_{2}(x,y)$都是连续函数，则有

$$\iiint_{V}f(x,y,z)\mathrm{d}x\mathrm{d}y\mathrm{d}z=\int_{x_{1}}^{x_{2}}\mathrm{d}x\int_{y_{1}(x)}^{y_{2}(x)}\mathrm{d}y\int_{z_{1}(x,y)}^{z_{2}(x,y)}f(x,y,z)\mathrm{d}z=\int_{x_{1}}^{x_{2}}\mathrm{d}x\iint_{S(x)}f(x,y,z)\mathrm{d}y\mathrm{d}z$$

(2) 变量代换

连续可微函数$x=x(u,v,w),y=y(u,v,w),z=z(u,v,w),\frac{\partial (x,y,z)}{\partial (u,v,w)}\neq 0$，则有

$$\iiint_{V}f(x,y,z)\mathrm{d}x\mathrm{d}y\mathrm{d}z=\iiint_{V}f\left[x(u,v,w),y(u,v,w),z(u,v,w)\right]\left|\frac{\partial (x,y,z)}{\partial (u,v,w)}\right|\mathrm{d}u\mathrm{d}v\mathrm{d}w$$

(a) 柱坐标系

$$x=r\cos\varphi\quad y=r\sin\varphi\quad z=h\quad \frac{\partial (x,y,z)}{\partial (\varphi,r,h)}=r$$

(b) 球坐标系

$$x=r\cos\varphi\cos\psi\quad y=r\sin\varphi\cos\psi\quad z=r\sin\psi\quad \frac{\partial (x,y,z)}{\partial (\varphi,\psi,r)}=r^{2}\cos\psi$$

(3) 质量

已知$\rho=\rho(x,y,z)$

$$M=\iiint_{V}\rho\mathrm{d}x\mathrm{d}y\mathrm{d}z$$

(4) 质心

$$\begin{aligned}&x_{0}=\frac{1}{M}\iiint\rho x\mathrm{d}x\mathrm{d}y\mathrm{d}z\ &y_{0}=\frac{1}{M}\iiint\rho y\mathrm{d}x\mathrm{d}y\mathrm{d}z\ &z_{0}=\frac{1}{M}\iiint\rho z\mathrm{d}x\mathrm{d}y\mathrm{d}z\end{aligned}$$

(5) 转动惯量

$$\begin{aligned}&I_{xy}=\iiint_{V}\rho z^{2}\mathrm{d}x\mathrm{d}y\mathrm{d}z\ &I_{yz}=\iiint_{V}\rho x^{2}\mathrm{d}x\mathrm{d}y\mathrm{d}z\ &I_{zx}=\iiint_{V}\rho y^{2}\mathrm{d}x\mathrm{d}y\mathrm{d}z\end{aligned}\qquad\begin{aligned}&I_{x}=I_{xy}+I_{xz}\ &I_{y}=I_{yx}+I_{yz}\ &I_{z}=I_{zx}+I_{zy} \end{aligned}\qquad \begin{aligned} &I_{l}=\iiint_{V}\rho r^{2}\mathrm{d}x\mathrm{d}y\mathrm{d}z\ &I_{0}=\iiint_{V}\rho(x^{2}+y^{2}+z^{2})\mathrm{d}x\mathrm{d}y\mathrm{d}z\ &I_{0}=I_{xy}+I_{yz}+I_{zx} \end{aligned}$$

(6) 引力势

$$u(x,y,z)=\iiint_{V}\rho(\xi,\eta,\zeta)\frac{\mathrm{d}\xi\mathrm{d}\eta\mathrm{d}\zeta}{r}$$

其中，$\rho:\rho(\xi,\eta,\zeta)$为物体的密度，且$r=\sqrt{(\xi-x)^{2}+(\eta-y)^{2}+(\zeta-z)^{2}}$，则有

$$\begin{aligned} &X=G\frac{\partial u}{\partial x}=G\iiint_{V}\rho\frac{\xi-x}{r^{3}}\mathrm{d}\xi\mathrm{d}\eta\mathrm{d}\zeta\ &Y=G\frac{\partial u}{\partial y}=G\iiint_{V}\rho\frac{\eta-y}{r^{3}}\mathrm{d}\xi\mathrm{d}\eta\mathrm{d}\zeta\ &Z=G\frac{\partial u}{\partial z}=G\iiint_{V}\rho\frac{\zeta-z}{r^{3}}\mathrm{d}\xi\mathrm{d}\eta\mathrm{d}\zeta\end{aligned}$$

其中，$G$为引力常数。

曲线积分

(1) 第一类曲线积分

若函数$f(x,y,z)$在平滑曲线$C$，$x=x(t),y=y(t),z=z(t),(t_{0}\leqslant t\leqslant T)$的各点上有定义并且连续，$\mathrm{d}s$为弧长的微分，则

$$\int_{C}f(x,y,z)\mathrm{d}s=\int_{t_{0}}^{T}f[x(t),y(t),z(t)]\sqrt{x_{t}^{\prime}+y_{t}^{\prime}+z_{t}^{\prime}}\mathrm{d}t$$

(2) 第二类曲线积分

若函数$P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)$在曲线上的各点是连续的，且曲线的方向是使参数$t$增加的方向，则

$$\int_{C}[P(x,y,z)\mathrm{d}x+Q(x,y,z)\mathrm{d}y+R(x,y,z)\mathrm{d}z]=\int_{t_{0}}^{T}[P[x(t),y(t),z(t)]x^{\prime}(t)+Q[x(t),y(t),z(t)]y^{\prime}(t)+R[x(t),y(t),z(t)]z^{\prime}(t)]\mathrm{d}t$$

(3) Green公式

设$C$为分段光滑的简单封闭围线，它围成单连通的有界区域$S$，并且当沿着围线正方向移动时，区域$S$保持在左边；此外，函数$P(x,y),Q(x,y)$及其一阶偏导数$P_{y}^{\prime}(x,y),Q_{x}^{\prime}(x,y)$在区域$S$内及其边界上皆是连续的，则成立Green公式

$$\oint_{C}\left[P(x,y)\mathrm{d}x+Q(x,y)\mathrm{d}y\right]=\iint_{S}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\mathrm{d}x\mathrm{d}y$$

若把区域$S$的边界$C$理解为一切边界之和，并且这样选取沿围线的环绕方向，使得区域$S$始终位于左边。

(4) 平面区域的面积

以分段光滑的简单围线$C$为界的图形的面积$S$等于

$$S=\oint_{C} x\mathrm{d}y-\oint_{C}y\mathrm{d}x=\frac{1}{2}\oint_{C}\left(x\mathrm{d}y-y\mathrm{d}x\right)=\frac{1}{2}\oint_{C}\left|\begin{matrix}x&y\ \mathrm{d}x&\mathrm{d}y\end{matrix}\right|$$

曲面积分

(1) 第一类曲面积分

若$S$为分片光滑的双侧曲面$x=x(u,v),y=y(u,v),z=z(u,v),((u,v)\in\Omega)$，而$f(x,y,z)$为在曲面$S$的各点上有定义并且连续函数，则

$$\iint_{S}f(x,y,z)\mathrm{d}S=\iint_{\Omega}f(x(u,v),y(u,v),z(u,v))\sqrt{EG-F^{2}}\mathrm{d}u\mathrm{d}v$$

$$E=\left(\frac{\partial x}{\partial u}\right)^{2}+\left(\frac{\partial y}{\partial u}\right)^{2}+\left(\frac{\partial z}{\partial u}\right)^{2}\quad F=\frac{\partial x}{\partial u}\frac{\partial x}{\partial v}+\frac{\partial y}{\partial u}\frac{\partial y}{\partial v}+\frac{\partial z}{\partial u}\frac{\partial z}{\partial v}\quad G=\left(\frac{\partial x}{\partial v}\right)^{2}+\left(\frac{\partial y}{\partial v}\right)^{2}+\left(\frac{\partial z}{\partial v}\right)^{2}$$

在特别情况下，若曲面的方程具有以下形式：

$$z=z(x,y)\qquad ((x,y)\in\sigma)$$

其中，$z(x,y)$为单值连续可微函数，则

$$\iint_{S}f(x,y,z)\mathrm{d}S=\iint_{\sigma}f\left[x,y,z(x,y)\right]\sqrt{1+\left(\frac{\partial z}{\partial x}\right)^{2}+\left(\frac{\partial z}{\partial y}\right)^{2}}\mathrm{d}x\mathrm{d}y$$

(2) 第二类曲面积分

若$S$为光滑的双侧面：$S^{+}$为它的正面，即由法向量$\vec{n}~[\cos\alpha,\cos\beta,\cos\gamma]$确定的一面，$P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)$为在曲面$S$上有定义而且连续的三个函数，则：

$$\iint_{S^{+}}\left(P\mathrm{d}y\mathrm{d}x+Q\mathrm{d}x\mathrm{d}z+R\mathrm{d}x\mathrm{d}y\right)=\iint_{S}\left(P\cos\alpha+Q\cos\beta+R\cos\gamma\right)\mathrm{d}S$$

若有参数方程$x=x(u,v),y=y(u,v),z=z(u,v)$，则法向量$\vec{n}$的方向余弦 由下列公式来确定

$$\begin{aligned} \cos\alpha&=\frac{A}{\pm\sqrt{A^{2}+B^{2}+C^{2}}}& \qquad\cos\beta&=\frac{B}{\pm\sqrt{A^{2}+B^{2}+C^{2}}}&\qquad\cos\gamma&=\frac{C}{\pm\sqrt{A^{2}+B^{2}+C^{2}}}\\ A&=\frac{\partial (y,z)}{\partial (u,v)}&\qquad B&=\frac{\partial (z,x)}{\partial (u,v)}&\qquad C&=\frac{\partial (x,y)}{\partial (u,v)}\qquad\end{aligned}$$

Stokes公式

若$P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)$为连续可微函数，$S$为分片光滑的有界双侧曲面，其边界$C$为分段光滑的简单封闭围线，则有Stokes公式：$$\oint_{C}\left(P\mathrm{d}x+Q\mathrm{d}y+R\mathrm{d}z\right)=\iint_{S}\left|\begin{matrix}\cos\alpha&\cos\beta&\cos\gamma\\ \frac{\partial}{\partial x}&\frac{\partial}{\partial y}&\frac{\partial}{\partial z}\\ P&Q&R \end{matrix} \right|\mathrm{d}S$$

Gauss公式

若空间区域$V$的边界$S$为分片光滑曲面，$P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)$和它们的一阶偏导数均为区域$V+S$内的连续函数，则有

$$\iint_{S}\left(P\cos\alpha+Q\cos\beta+R\cos\gamma\right)\mathrm{d}S=\iiint_{V}\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right)\mathrm{d}x\mathrm{d}y\mathrm{d}z$$

其中，$\cos\alpha,\cos\beta,\cos\gamma$为曲面$S$的外法线的方向余弦。