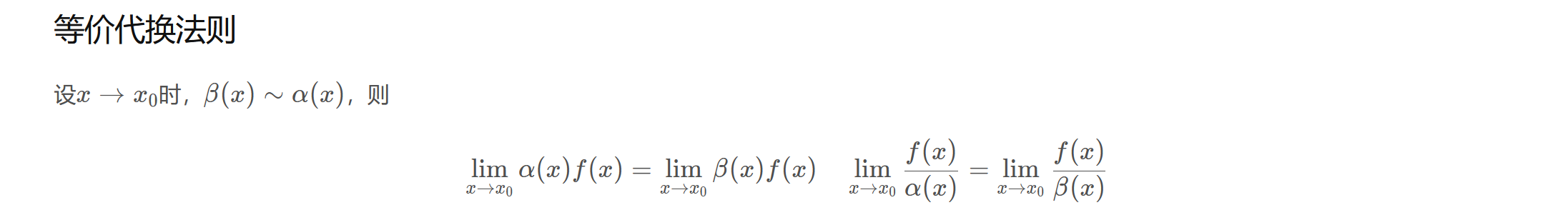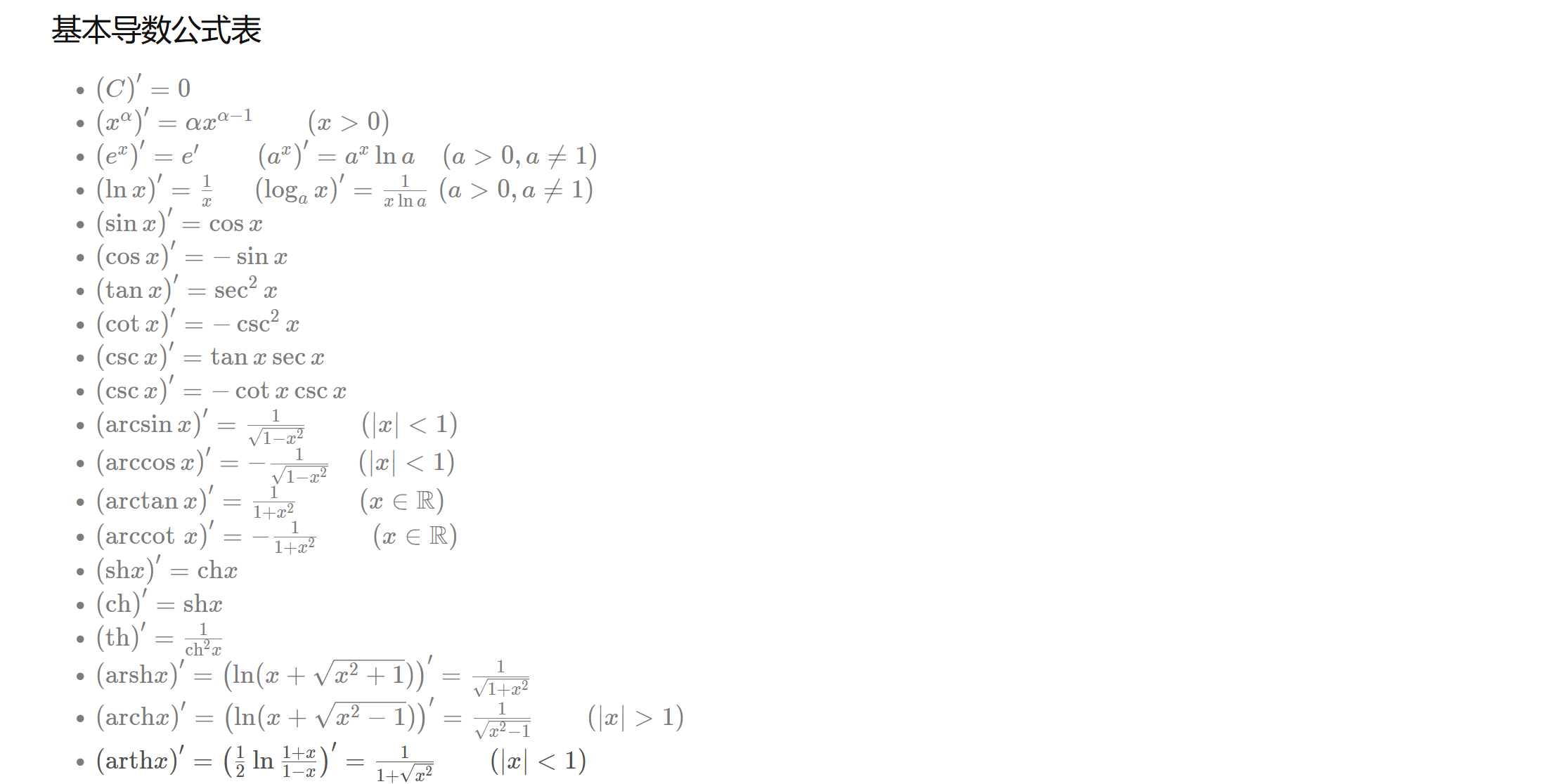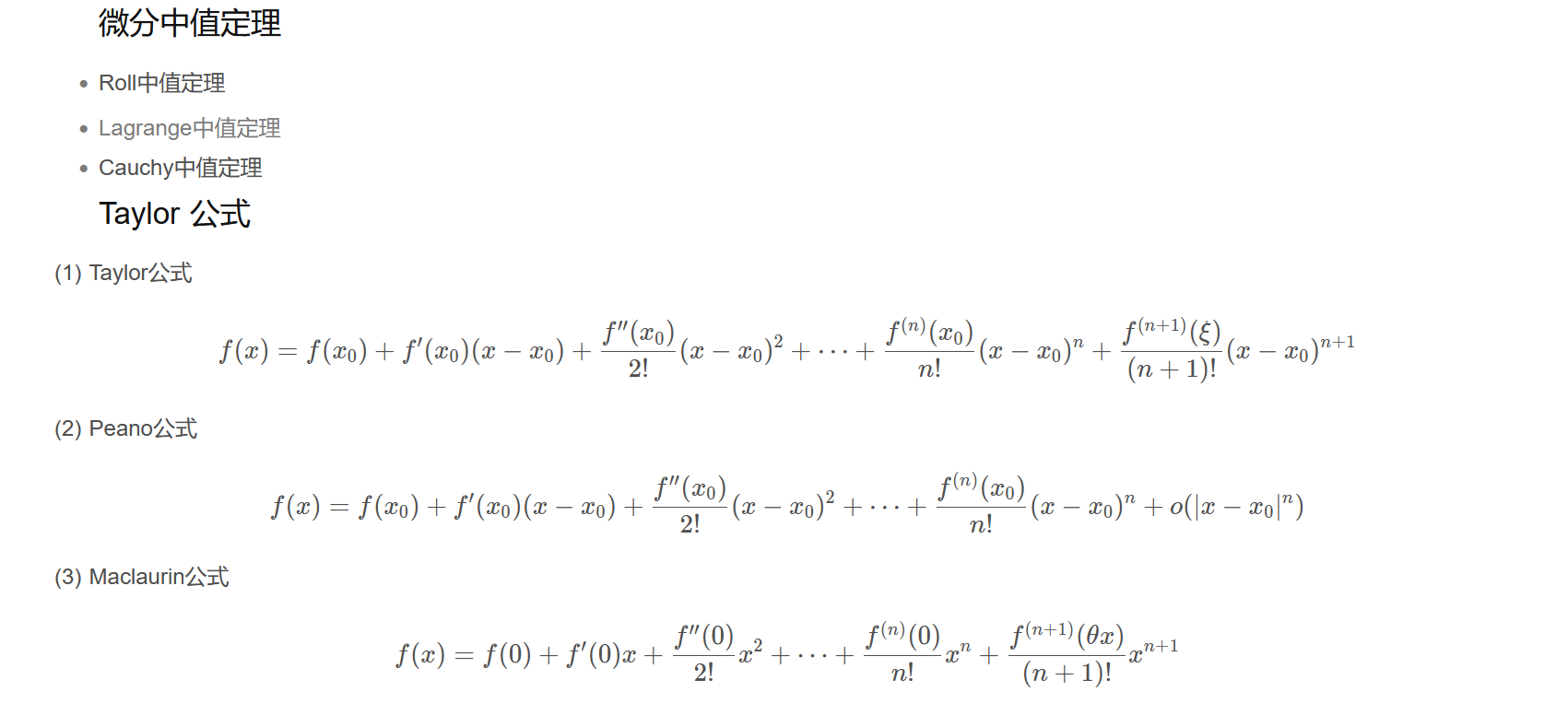常用不等式

(1) 三角不等式

$$\left|x-y\right|\leqslant\left|x-z\right|+\left|z-y\right|$$

(2) 平均不等式

设$x_{1},x_{2},\ldots,x_{n}>0$，则有

$$\frac{n}{\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}}}\leqslant\sqrt[n]{x_{1}x_{2}\cdots x_{n}}\leqslant\frac{x_{1}+x_{2}+\cdots+x_{n}}{n}$$

(3) 面积不等式

$$\cos x<\frac{\sin x}{x}<1$$

(4) 压缩不等式

$$\left|\sin x-\sin y\right|\leqslant\left|x-y\right|$$$$\left|\cos x-\cos y\right|\leqslant\left|x-y\right|$$

(5) 阶乘不等式

$$\begin{aligned}2^{n}<&n!<\left(\frac{n+1}{2}\right)^{n}\qquad (n>4) \\ n!&\geqslant n^{\frac{n}{2}}\end{aligned}$$

(6) 乘幂不等式

$$\begin{aligned}\left(1+\frac{1}{n}\right)^{n}&<3\ \left(1+\frac{1}{n}\right)^{n}&<\left(1+\frac{1}{n+1}\right)^{n+1}\ \left(1+x\right)^{n}&\geqslant 1+nx\qquad(x\geqslant 0)\ \left(1+x\right)^{n}&\geqslant\frac{n^{2}}{4}x^{2}\qquad~~(x\geqslant 0\quad n\geqslant 2)\end{aligned}$$

(7) 夹挤不等式

$$\begin{aligned}2\left(\sqrt{n+1}-\sqrt{n}\right)&<\frac{1}{\sqrt{n}}<2\left(\sqrt{n}-\sqrt{n+1}\right)\ \ln\left(1+\frac{1}{n}\right)&<~~\frac{1}{n}~<\ln\left(1+\frac{1}{n-1}\right)\end{aligned}$$

(8) Jordan不等式

设$0<x<\frac{\pi}{2}$，则

$$\frac{\pi}{2}<\frac{\sin x}{x}<1$$$$\frac{x^{2}}{\pi}<1-\cos x<\frac{x^{2}}{2}$$

(9) Jensen不等式

设$f(x)$在$(a,b)$区间内有二阶导数。若$x\in(a,b)$时，$f^{\prime\prime}(x)>0$，则$x_{1},x_{2},\ldots,x_{n}\in(a,b)$时，恒有

$$f\left(\sum_{i=1}^{n}t_{i}x_{i}\right)\leqslant\sum_{i=1}^{n}t_{i}f(x_{i})$$

且当且仅当$x_{1}=x_{2}=\cdots=x_{n}$时等号成立。其中，$t_{i}>0~(i=1,2,\ldots,n)$且$\sum\limits_{i=1}^{n}t_{i}=1$。

(9) 下凸函数不等式

设$f(x)$是$(a,b)$区间内的下凸函数，若$a<x<y<z<b$，则有

(a) 面积不等式

$$\left|\begin{matrix}x&f(x)&1\\ y&f(y)&1\\ z&f(z)&1\end{matrix}\right|\geqslant 0$$

(b) 差商不等式

$$\frac{f(y)-f(x)}{y-x}\leqslant\frac{f(z)-f(x)}{z-x}\leqslant\frac{f(z)-f(y)}{z-y}$$

(c) 斜率不等式$$f_{-}^{\prime}(x)\leqslant f_{+}^{\prime}(x)$$

(d) 斜率——差商不等式

$$f_{+}^{\prime}(x)\leqslant\frac{f(y)-f(x)}{y-x}\leqslant f_{-}^{\prime}(y)$$

(11) Cauchy不等式

设$a_{i}>0,b_{i}>0,(i=1,2,\ldots,n)$，则

$$\sum_{i=1}^{n}a_{i}b_{i}\leqslant\left(\sum_{i=1}^{n}a_{i}^{p}\right)^{\frac{1}{p}}\left(\sum_{i=1}^{n}b_{i}^{q}\right)^{\frac{1}{q}}$$

其中，$p>0,q>0,\frac{1}{p}+\frac{1}{q}=1$。

(12) Yong不等式

设$A\geqslant0,B\geqslant0,p>0,q>0$且$\frac{1}{p}+\frac{1}{q}=1$，则

$$AB\leqslant \frac{1}{p}A^{p}+\frac{1}{q}B^{q}$$

(13) Hölder不等式

设$p>0,q>0,\frac{1}{p}+\frac{1}{q}=1$，若$f(x),g(x)$在$[a,b]$上可积，则

$$\int_{a}^{b}\left|f(x)g(x)\right|\mathrm{d}x\leqslant\left(\int_{a}^{b}\left|f(x)\right|^{p}\mathrm{d}x\right)^{\frac{1}{p}}\left(\int_{a}^{b}\left|g(x)\right|^{q}\mathrm{d}x\right)^{\frac{1}{q}}$$

(14) Minkowski不等式

设$p>1$，若$f(x),g(x)$在$[a,b]$上可积，则

$$\left(\int_{a}^{b}\left|f(x)+g(x)\right|^{p}\mathrm{d}x\right)^{\frac{1}{p}}\leqslant\left(\int_{a}^{b}\left|f(x)\right|^{p}\mathrm{d}x\right)^{\frac{1}{p}}+\left(\int_{a}^{b}\left|g(x)\right|^{p}\mathrm{d}x\right)^{\frac{1}{p}}$$

(15) Gronwall不等式

设$a,b>0$，$f(x)$在$[0,+\infty)$上非负连续，若$x\geqslant 0$时，$f(x\leqslant a+b\int_{0}^{x}f(t)\mathrm{d}t)$，则$x\geqslant 0$时，必有$f(x)\leqslant a e^{bx}$。

(16) Abel不等式

(a) (有限形式) 设$a_{0}\geqslant a_{1}\geqslant \cdots \geqslant a_{n}\geqslant 0$，则

$$m a_{0}\leqslant a_{0}b_{0}+a_{1}b_{1}+\cdots+a_{n}b_{n}\leqslant M a_{0}$$

(b) (积分形式) 设$f(x)$是$[a,b]$上的非负减函数，$g(x)$是$[a,b]$上的可积函数，则

$$m f(a)\leqslant\int_{a}^{b}f(x)g(x)\mathrm{d}x\leqslant M f(a)$$

等价公式

设$x\to x_{0}$，$\omega(x)\to,\neq 0$，则$x\to x_{0}$时，必有

• $\sin\omega(x)\sim\omega(x)$
• $\omega(x)-\sin\omega(x)\sim\frac{1}{6}\omega^{3}(x)$
• $\ln\left(1+\omega(x)\right)\sim\omega(x)$
• $\omega(x)-\ln(1+\omega(x))\sim\frac{1}{2}\omega^{2}(x)$
• $e^{\omega(x)}-1\sim\omega(x)$
• $e^{\omega(x)}-1-\omega(x)\sim\frac{1}{2}\omega^{2}(x)$
• $1-\cos\omega(x)\sim\frac{1}{2}\omega^{2}(x)$
• $\left(1+\omega(x)\right)^{\alpha}-1\sim\alpha\omega(x)\qquad(\alpha\neq 0)$
• $\arcsin\omega(x)-\omega(x)\sim\frac{1}{6}\omega^{3}(x)$
• $\frac{\pi}{2}-\arccos\omega(x)-\omega(x)\sim\frac{1}{6}\omega^{3}(x)$
• $\tan\omega(x)-\omega(x)\sim\frac{1}{3}\omega^{3}(x)$
• $\omega(x)-\arctan\omega(x)\sim\frac{1}{3}\omega^{3}(x)$
• $\tan\omega(x)\sim\omega(x)$

等价代换法则

设$x\to x_{0}$时，$\beta(x)\sim \alpha(x)$，则$$\lim\limits_{x\to x_{0}}\alpha(x)f(x)=\lim\limits_{x\to x_{0}}\beta(x)f(x)\quad\lim\limits_{x\to x_{0}}\frac{f(x)}{\alpha(x)}=\lim\limits_{x\to x_{0}}\frac{f(x)}{\beta(x)}$$

基本导数公式表

• $\left(C\right)^{\prime}=0$
• $\left(x^{\alpha}\right)^{\prime}=\alpha x^{\alpha-1}\qquad (x>0)$
• $\left(e^{x}\right)^{\prime}=e^{\prime}\qquad \left(a^{x}\right)^{\prime}=a^{x}\ln a\quad(a>0,a\neq 1)$
• $\left(\ln x\right)^{\prime}=\frac{1}{x}~\quad\left(\log_{a}x\right)^{\prime}=\frac{1}{x\ln a}~(a>0, a\neq 1)$
• $\left(\sin x\right)^{\prime}=\cos x$
• $\left(\cos x\right)^{\prime}=-\sin x$
• $\left(\tan x\right)^{\prime}=\sec^{2}x$
• $\left(\cot x\right)^{\prime}=-\csc^{2}x$
• $\left(\csc x\right)^{\prime}=\tan x\sec x$
• $\left(\csc x\right)^{\prime}=-\cot x\csc x$
• $\left(\arcsin x\right)^{\prime}=\frac{1}{\sqrt{1-x^{2}}}\qquad (|x|<1)$
• $\left(\arccos x\right)^{\prime}=-\frac{1}{\sqrt{1-x^{2}}}\quad (|x|<1)$
• $\left(\arctan x\right)^{\prime}=\frac{1}{1+x^{2}}~\qquad(x\in\mathbb{R})$
• $\left(\mathrm{arccot}~ x\right)^{\prime}=-\frac{1}{1+x^{2}}\qquad(x\in\mathbb{R})$
• $\left(\mathrm{sh}x\right)^{\prime}=\mathrm{ch}x$
• $\left(\mathrm{ch}\right)^{\prime}=\mathrm{sh}x$
• $\left(\mathrm{th}\right)^{\prime}=\frac{1}{\mathrm{ch}^{2}x}$
• $\left(\mathrm{arsh}x\right)^{\prime}=\left(\ln(x+\sqrt{x^{2}+1})\right)^{\prime}=\frac{1}{\sqrt{1+x^{2}}}$
• $\left(\mathrm{arch}x\right)^{\prime}=\left(\ln(x+\sqrt{x^{2}-1})\right)^{\prime}=\frac{1}{\sqrt{x^{2}-1}}\qquad(|x|>1)$

• $\left(\mathrm{arth}x\right)^{\prime}=\left(\frac{1}{2}\ln\frac{1+x}{1-x}\right)^{\prime}=\frac{1}{1+\sqrt{x^{2}}}\qquad(|x|<1)$

  导数运算法则

• $\left(u\pm v\right)^{\prime}=u^{\prime}\pm v^{\prime}$

• $\left(u\cdot v\right)^{\prime}=u^{\prime}\cdot v+u\cdot v^{\prime}$

• $\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}\cdot v-u\cdot v^{\prime}}{v^{2}}$

• $f^{\prime}(x)=\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{1}{\frac{\mathrm{d}x}{\mathrm{d}y}}=\frac{1}{\varphi^{\prime}(y)}=\frac{1}{\varphi^{\prime}(f(x))}$

• $\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y}{\mathrm{d}u}\cdot\frac{\mathrm{d}u}{\mathrm{d}x}$

  基本微分公式表

• $\mathrm{d}~C=0$

• $\mathrm{d}~x^{\alpha}=\alpha x^{\alpha-1}~\mathrm{d}x$

• $\mathrm{d}~a^{x}=a^{x}\ln a~\mathrm{d}x$

• $\mathrm{d}~e^{x}=e^{x}~\mathrm{d}x$
• $\mathrm{d}\log_{a} x=\frac{1}{x\ln a}~\mathrm{d}x$
• $\mathrm{d}\ln x=\frac{1}{x}~\mathrm{d}x$
• $\mathrm{d}\sin x=\cos x~\mathrm{d}x$
• $\mathrm{d}\cos x=-\sin x~\mathrm{d}x$
• $\mathrm{d}\tan x=\sec^{2}x~\mathrm{d}x$
• $\mathrm{d}\cot x=-\csc^{2}x~\mathrm{d}x$
• $\mathrm{d}\sec x=\sec x\tan x~\mathrm{d}x$
• $\mathrm{d}\csc x=-\csc x\cot x~\mathrm{d}x$
• $\mathrm{d}\arcsin x=\frac{1}{\sqrt{1-x^{2}}}~\mathrm{d}x$
• $\mathrm{d}\arccos x=-\frac{1}{\sqrt{1-x^{2}}}~\mathrm{d}x$
• $\mathrm{d}\arctan x=\frac{1}{1+x^{2}}~\mathrm{d}x$

• $\mathrm{d}~\mathrm{arccot}~ x=-\frac{1}{1+x^{2}}~\mathrm{d}x$

  基本积分表(C为常数)

• $\int k~\mathrm{d}x=kx+C \qquad(k$为常数)

• $\int x^{\mu}~\mathrm{d}x=\frac{1}{\mu+1}x^{\mu+1}+C~~(\mu\neq -1)$

• $\int\frac{1}{x}~\mathrm{d}x=\ln|x|+C$
• $\int e^{x}~\mathrm{d}x=e^{x}+C$
• $\int a^{x}~\mathrm{d}x=\frac{a^{x}}{\ln a}+C~~~\qquad(a>0,a\neq 1)$
• $\int \cos x~\mathrm{d}x=\sin x+C$
• $\int \sin x~\mathrm{d}x=-\cos x+C$
• $\int\frac{1}{\cos^{2}x}~\mathrm{d}x=\int\sec^{2}x~\mathrm{d}x=\tan x+C$
• $\int\frac{1}{\sin^{2}x}~\mathrm{d}x=\int\csc^{2} x~\mathrm{d}x=-\cot x+C$
• $\int\sec x\tan x~\mathrm{d}x=\sec x+C$
• $\int\csc x\cot x~\mathrm{d}x=-\csc x+C$
• $\int \mathrm{sh}x~\mathrm{d}x=\mathrm{ch}x+C$
• $\int\mathrm{ch}x~\mathrm{d}x=\mathrm{sh}x+C$
• $\int\frac{1}{1+x^{2}}~\mathrm{d}x=\arctan x+C$
• $\int\frac{1}{a^{2}+x^{2}}~\mathrm{d}x=\frac{1}{a}\arctan\frac{x}{a}+C \qquad (a>0)$
• $\int\frac{1}{1-x^{2}}~\mathrm{d}x=\frac{1}{2}\ln\left|\frac{1+x}{1-x}\right|+C$
• $\int\frac{1}{a^{2}-x^{2}}~\mathrm{d}x=\frac{1}{2a}\ln\left|\frac{a+x}{a-x}\right|+C \qquad(a>0)$
• $\int\tan x~\mathrm{d}x=-\ln\left|\cos x\right|+C$
• $\int\cot x~\mathrm{d}x=\ln\left|\sin x\right|+C$
• $\int\sec x~\mathrm{d}x=\ln\left|\sec x+\tan x\right|+C$
• $\int\csc x~\mathrm{d}x=\ln\left|\csc x-\cot x\right|+C$
• $\int\frac{1}{\sqrt{1-x^{2}}}~\mathrm{d}x=\arcsin x+C$
• $\int\frac{1}{\sqrt{a^{2}-x^{2}}}~\mathrm{d}x=\arcsin\frac{a}{x}+C \qquad (a>0)$
• $\int\sqrt{a^{2}-x^{2}}~\mathrm{d}x=\frac{x}{2}\sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2}\arcsin\frac{x}{a}+C\qquad (a>0)$
• $\int\frac{1}{\sqrt{x^{2}\pm 1}}~\mathrm{d}x=\ln\left|x+\sqrt{x^{2}\pm 1}\right|+C$
• $\int\frac{1}{\sqrt{x^{2}+a^{2}}}~\mathrm{d}x=\ln\left|x+\sqrt{x^{2}\pm a^{2}}\right|+C~~(a>0)$
• $\int\sqrt{x^{2}+a^{2}}~\mathrm{d}x=\frac{x}{2}\sqrt{x^{2}+a^{2}}\pm\frac{a^{2}}{2}\ln\left|x+\sqrt{x^{2}\pm a^{2}}\right|+C\qquad (a>0)$
• $\int\ln x~\mathrm{d}x=x\ln x-x+C$
• $\int\arcsin x~\mathrm{d}x=x\arcsin x+\sqrt{1-x^{2}}+C$
• $\int\arccos x~\mathrm{d}x=x\arccos x-\sqrt{1-x^{2}}+C$

• $\int\arctan x~\mathrm{d}x=x\arctan x-\frac{1}{2}\ln(1+x^{2})+C$

  微分中值定理

• Roll中值定理

• Lagrange中值定理

• Cauchy中值定理

  Taylor 公式

(1) Taylor公式$$f(x)=f(x_{0})+f^{\prime}(x_{0})(x-x_{0})+\frac{f^{\prime\prime}(x_{0})}{2!}(x-x_{0})^{2}+\cdots+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}+\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-x_{0})^{n+1}$$

(2) Peano公式$$f(x)=f(x_{0})+f^{\prime}(x_{0})(x-x_{0})+\frac{f^{\prime\prime}(x_{0})}{2!}(x-x_{0})^{2}+\cdots+\frac{f^{(n)}(x_{0})}{n!}(x-x_{0})^{n}+o(|x-x_{0}|^{n})$$

(3) Maclaurin公式$$f(x)=f(0)+f^{\prime}(0)x+\frac{f^{\prime\prime}(0)}{2!}x^{2}+\cdots+\frac{f^{(n)}(0)}{n!}x^{n}+\frac{f^{(n+1)}(\theta x)}{(n+1)!}x^{n+1}$$