共7条回复
时间正序
- 时间正序
- 时间倒序
- 评论最多
3条评论 评论
- 1
还没有昵称
1年前
2024-12-1 08:34:04
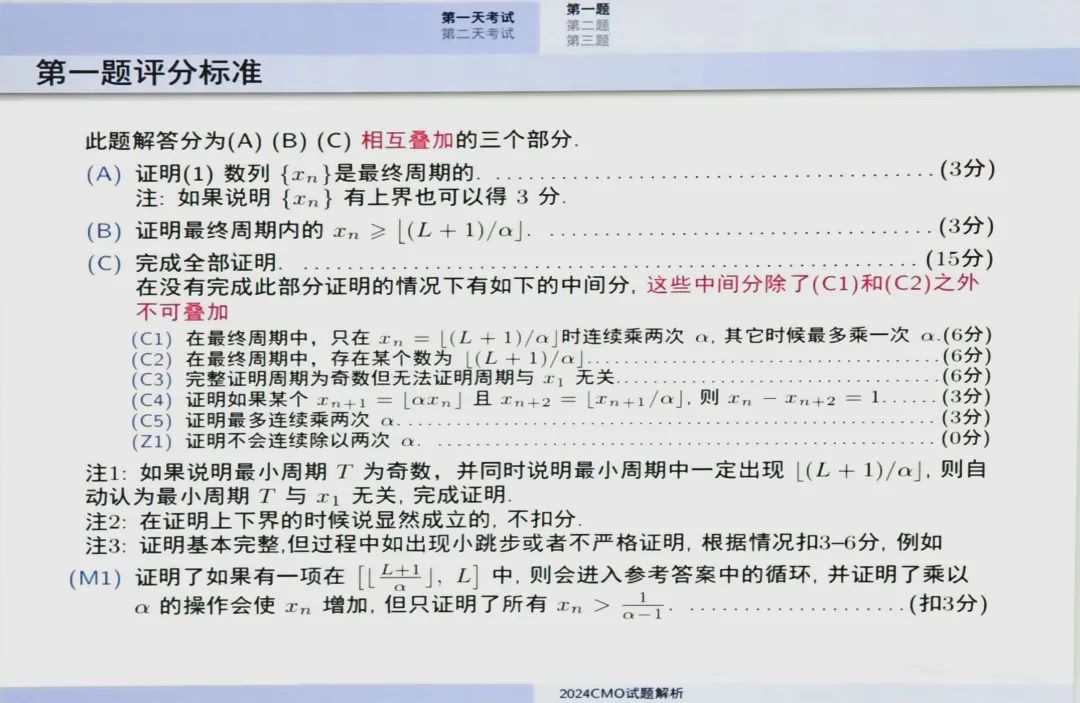
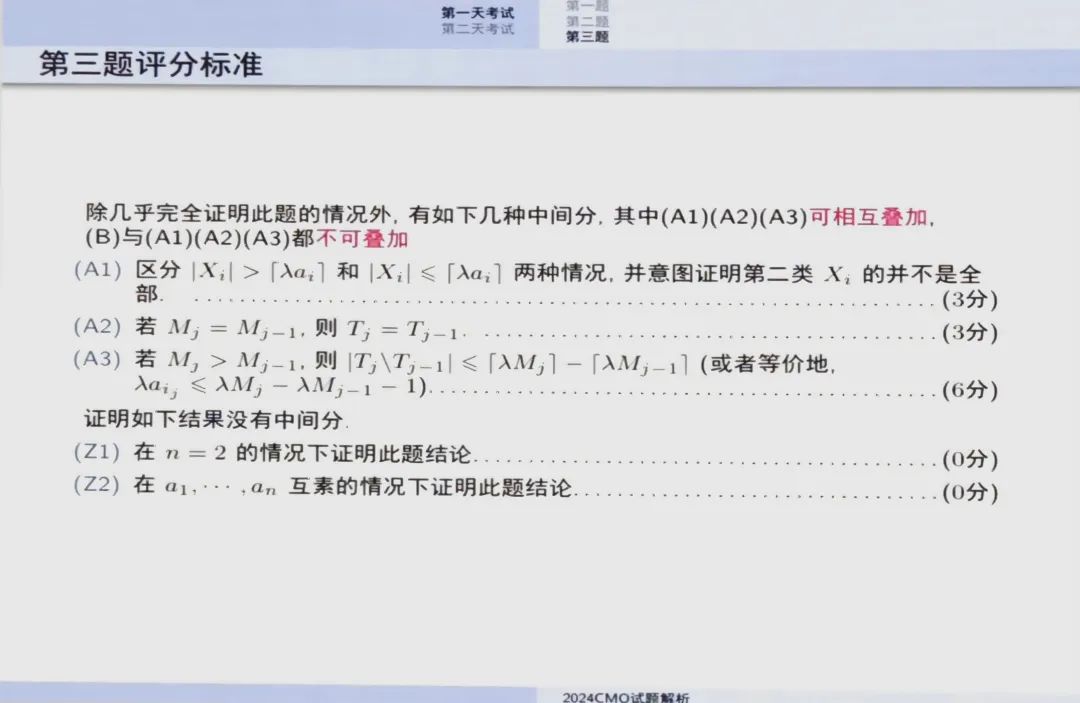
宣告第三题结束
草率的随便写了一下解析,但是发现自己写了个屎样就不发出来了
思路:利用极小集 X 的性质和分数部分的求和特性来限制集合 X 的大小,定义函数 f(X) 为集合 X 中所有元素关于 $a_i $的分数部分和的最小值。首先考虑 $M=a_1 $的情况,利用分数部分的下界来直接得出$ f(X) \geq \frac{|X|}{M} $。接着,对于 $M > a_1 $的情况,考虑集合$ X' = X \setminus P $,其中 P 是由不在$ X_i $中的元素构成的集合,分数部分的求和不等式,推导出 |X'| 的上界。再分析 X' 中元素的分数部分和,结合$ f(X) \geq \frac{2}{a_n} $的条件,最终得出 $|X| \leq f(X)M$






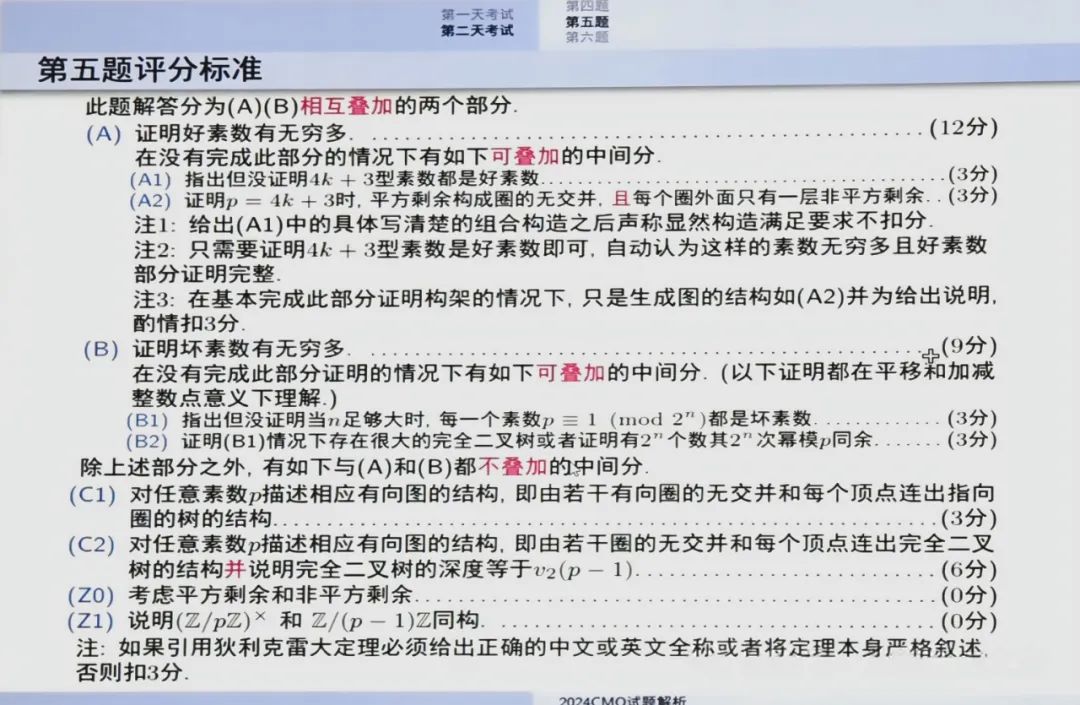
 给大佬们练手
给大佬们练手

