物理

关于n个扇形的k染色问题

染色问题是组合问题中一种极其常见的题型，本人不才，斗胆与大家分享一下自己的看法

完整题目为“用k种不同的颜色给n个扇环(如图1所示)进行染色，保证相邻扇形的颜色不同，其方法数$a_n$为多少？”

对于此类问题我们可以先进行枚举，寻找规律，随后进行推广。当$n=4$时，将扇环按顺时针编号1~4(如图2所示)

为方便讨论，将圆排列为改为直线排列(如图3所示)(注:1和4本质上是相邻的)

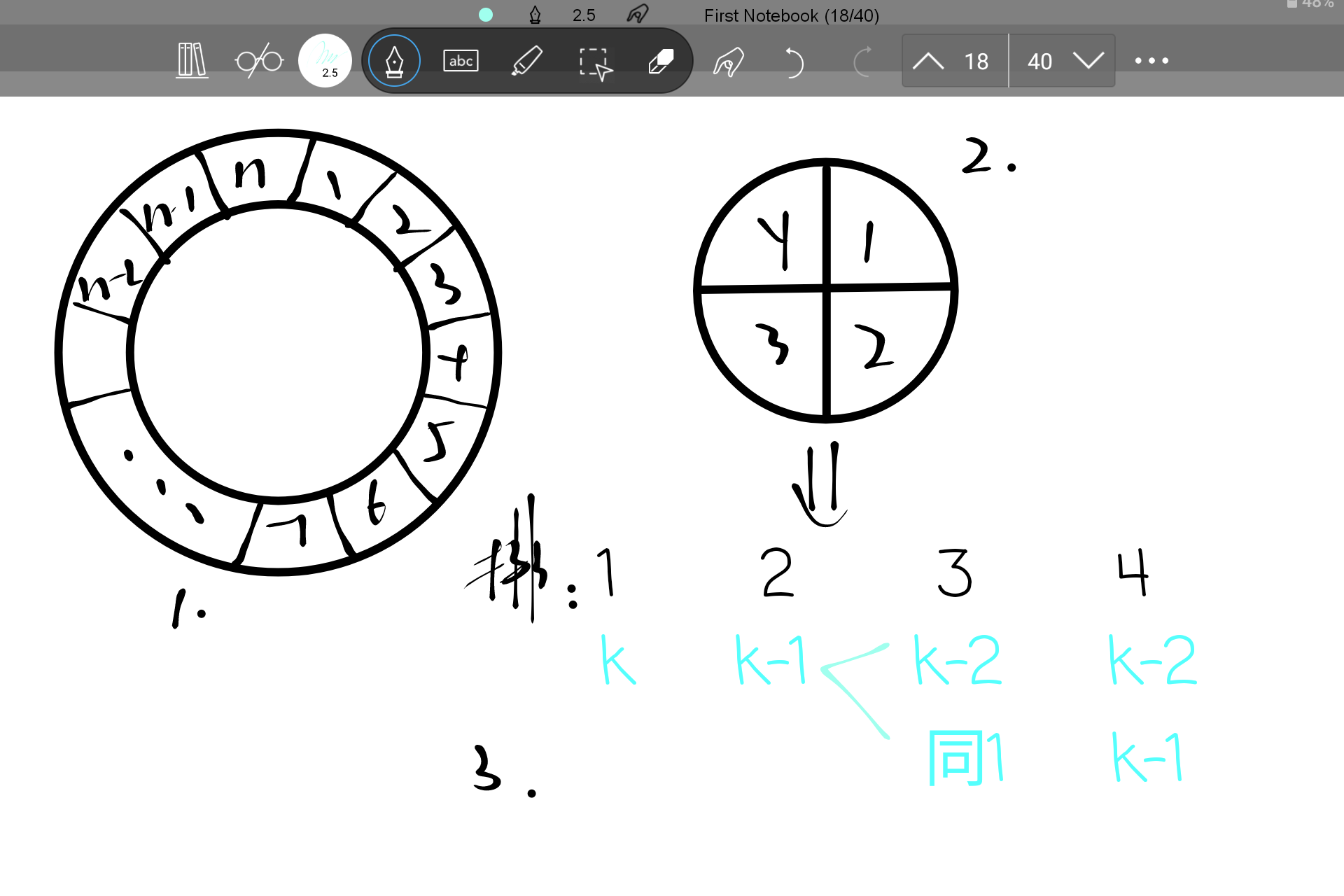
则显然1有$k$种情况，1确定后2仅剩$k-1$种情况，3也如此。

但3较为特殊，若3和1颜色相同，那么4的选择便是$k-1$种(因为4的选择与3和1不同，而3和1相同)

反之，则4的选择是$k-2$种。故分类讨论，将ⅰ和j颜色相同令为$C_i=C_j$，反之则$C_i≠C_j$，ⅰ的颜色种类数令为$A(ⅰ)$

①$C_1=C_3$，则$A(1)=A(3)=k$，且颜色一一对应，故不用重复计算，而$A(2)=A(4)=k-1$

所以此类方法是由乘法原理可知为$\prod_{i=1}^4A(i)=k(k-1)^2$

②$C_1≠C_3$，又$C_3≠C_2$，故$A(1)=k$，$A(2)=k-1$，$A(3)=A(4)=k-2$

由乘法原理可知此时方法数为$\prod_{j=1}^4A(j)=k(k-1)(k-2)^2$

∴由加法原理可知$a_4=k(k-1)(k-2)^2+k(k-1)^2=(k-1)(k-1+1)[(k-1)^2-(k-1)+1]=(k-1)^4+(k-1)$

当$n=5$时，依照上述方法可得出上表，同理可得$a_5=k(k-1)(k-2)^2+2k(k-1)^2(k-2)$

$=k(k-1)(k-2)[(k-1)^2+1]=(k-1)[(k-1)^4-1]=(k-1)^5-(k-1)$

当$n=6$时，也有$a_6=k(k-1)(k-2)^4+3k(k-1)^2(k-2)^2+k(k-1)^3$

$=k(k-1)[(k-2)^4+3(k-1)(k-2)^2+(k-1)^2]=(k-1)[(k-1)^5+1]=(k-1)^6+(k-1)$

当然还可以继续列举下去，不过已经没必要了

依据$a_4$，$a_5$，$a_6$我们已经可以大致推测出$a_n$与n的奇偶性有关

其公式应为$a_n=(k-1)^n+(-1)^n(k-1)$①

不光如此，观察我用红笔和蓝笔圈出的部分，会发现红圈部分与$a_5$的列举情况相等，蓝圈部分与$a_4$的列举情况相等

这是巧合吗？不，如果再多枚举，也可以发现同样的规律。于是乎我们似乎可以得到这样的关系:

$a_n=(k-2)a_{n-1}+(k-1)a_{n-2}$②

观察式子①，还可以得出:$a_n+a_{n-1}=k(k-1)^{n-1}$③

对数列敏感的人已经可以意识到，②和③可以看作是一种递推公式，而①则是我们要求的通项公式

既然我们直接求出通项很困难，无法一步登天

那为何不退而求其次，先确定递推公式，以此为转折点，再一步步推出通项呢？

我们对于数列已经很熟悉了，那么把我们的老朋友请出来解决新问题，这何尝不是一种化归思想？

Ok，现在证明思路已经有了，需要证明的结论也基本确定了，那么接下来，我们所需要的，便是严谨的证明。

证明:(运用②)

假定$a_{n-1}$和$a_{n-2}$已知($n-1$为奇数)，分别设为$A和B$

对$n-1$个圆环进行顺时针标号$1$~$n-1$

在$n-1$个扇环基础上再加一个扇环（为$n$号），故$A(n)=k-2或k-1$

当$A(n)=k-2$时，显然有$C_{n-1}≠C_1$

∵$n-1$为奇数，∴此时$A(n-1)$较于$a_{n-1}$中不变

∴$A(n-2)$不变，故依此可得$A(1一n-2)$均不会改变，因此可看做$a_{n-1}$的各类情况方法数乘上$k-2$

∴此情况下的方法数为$(k-2)A$

当$A(n)=k-1$时，显然有$C_{n-1}=C_1$，故$C_{n-2}≠C_1$

∴此时$A(n-2)$较于$a_{n-2}$中不变

∴$A(n-3)$不变，故依此可得$A(1一n-3)$均不会改变，因此可看做$a_{n-2}$的各类情况方法数乘上$k-1$

∴此情况下的方法数为$(k-1)B$

∴有$a_n=(k-2)a_{n-1}+(k-1)a_{n-2}$，设它的特征根方程为$x^2=(k-2)x+(k-1)$

∴则两根为$-1$，$-(k-1)$

∴设其通项为$a_n=α(k-1)^n+β(-1)^n$，带入$a_1=0$，$a_2=k(k-1)$

得到$α=1$，$β=(k-1)$

∴$a_n=(k-1)^n+(-1)^n(k-1)$   

当$n-1$为偶数时同理， 故Q.E.D

本人不是大佬，证明过程可能不严谨，用词可能不准，望谅解

除了上述方法，我们还可以用推出$a_4$的方法推$a_n$

这里直接放结果了:n为偶数，$a_n=\sum_{m=1}^{\dfrac{n-2}{2}}C_{n-2-m}^mk(k-1)^m(k-2)^{n-2-2m}$

n为奇数的时候，请读者自证

完。