大家好呀，我是健康码。我曾在化竞的小圈子里活跃了一段时间，也非常喜欢钻研物理和化学（虽然到现在都还只是一个蒟蒻）。在学习化学和物理的过程中难免会看到一些让人头大的∫和d，这些高中从来没讲过，大学教材又喜欢默认你会的东西就是微积分，在物理和化学（尤其是化学）并不需要你真正的从严谨的纯数学角度证明和运用微积分，你只需要理解1.啥是微积分2.啥时候要用微积分3.怎么用微积分。就可以完美解决学习初期所遇到的哪些让人摸不到头脑的微积分式子。

下面让我们以半理解半证明的方式，了解一下微积分吧

1.何为函数：

从小学开始，我们就开始接触各类函数，比如速度和时间的函数关系，吃的饭和长的体重的函数关系......这其中最关键的词其实是关系！！

没错！函数的本质是两个东西之间的关系--------------a通过一种关系f变化成了b，这就是一种关系。一群的a和一群的b通过关系f相互对应，这也是一种关系。

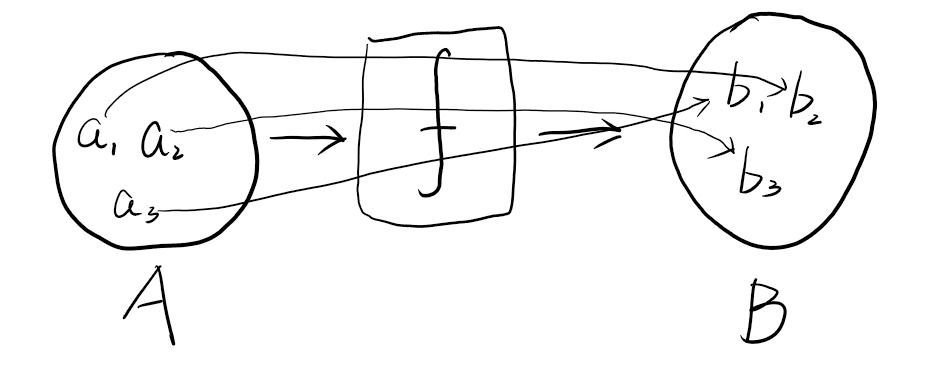
函数就像是一个工厂，将a加工成b！下面我们对工厂的各个部分进行定义：

所有的a构成的集合A就叫做函数的定义域，所有b构成的集合B就叫函数的值域，被加工的a称为函数的自变量，加工得到的产品b称为函数的因变量。

用x和y替换其中的a和b，x和y的关系仍然是f，此时我们就可以把函数记作最常见的形式y=f（x）！

用一个平面直角坐标系就可以将函数转化为函数图像

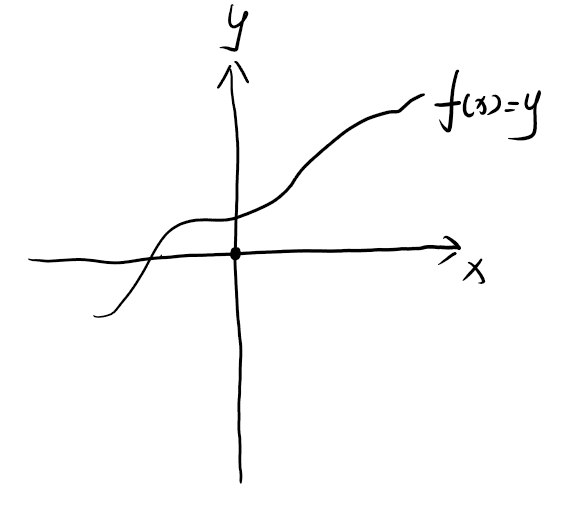
2.何为连续：

我们在小学都知道，对于有理数来说，任意取有理数a>b，总会有无数个有理数在a和b之间。这不关乎a和b相差到底有多少，只要a≠b，那么总会有其他有理数在a和b之间。有理数的这种性质叫做稠密性，拓展到实数，还是存在这种稠密性。稠密性就代表了一个集合A中的数在数轴上总是牵连不断的，A中的任意两个数可以无限的靠近（两数的差无限小）例如下图：

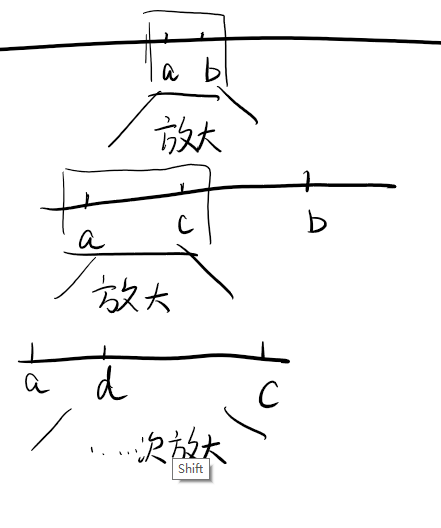
来到函数中，如果定义域是稠密的，则函数的自变量x都是连续不断的。在此基础上，如果按照某一段定义域上自变量x大小的顺序排列时对应的因变量y=f（x）组成的集合是有序（前大后小或前小后大）且稠密的，就称这个函数在这一段定义域上是连续的！

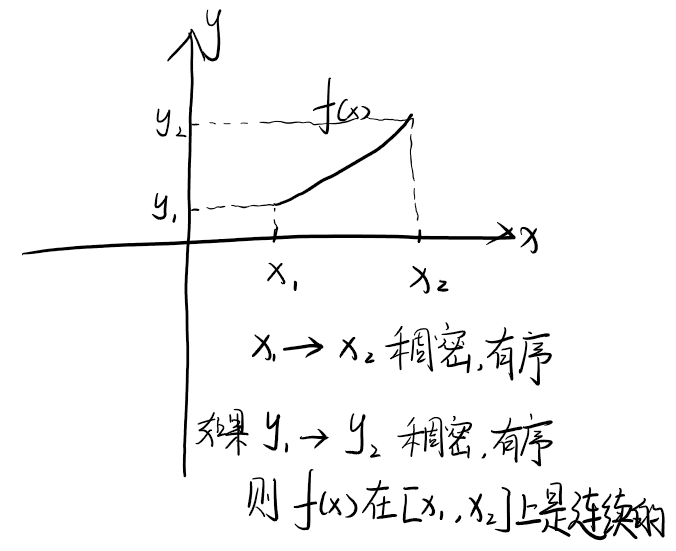
如果将函数的定义域分成好多这样的小段（区间），函数在每个小段都是连续的，而且每个小段的开头x和结尾x对应的y都是相同的，则每段连续的函数可以拼接起来成一个，此时函数就在整个定义域上连续！就如下图一样（有一点像拼积木）

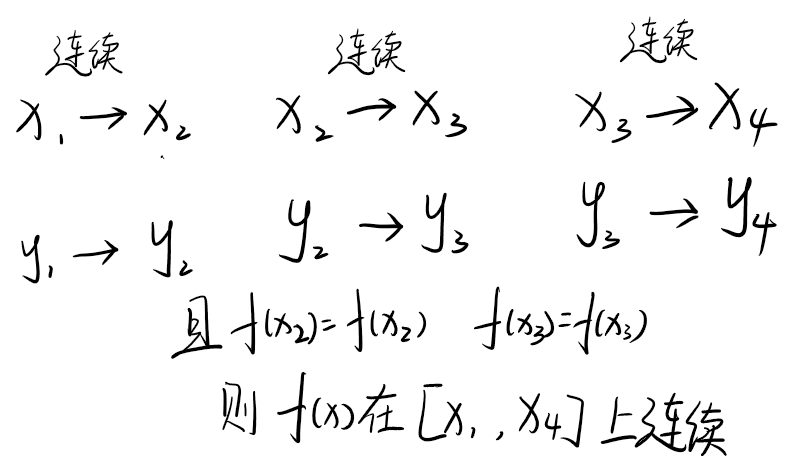
3.附近与逼近：

4.函数的极限：

5.变化与变化率：

6.微分与导数：

7.求和与定积分：

8.半定积分与不定积分：

9.多元函数与偏导数

施工线（正在施工）

安全声明

本贴偏向于科普，多面向微积分小白（虽然我也是），其中我会尽量不使用超过初中水平的概念。

本贴的严谨性是低于科普性的，各位大佬多多担待。本人也是个蒟蒻，在哪里如果存在讲述的问题请及时指出我会及时修正和学习。

本贴的讲解顺序不是按照高数或其他微积分的章节顺序进行的，旨在梳理微积分的基本知识。

希望看完本贴可以有助于童鞋们对微积分的进一步学习