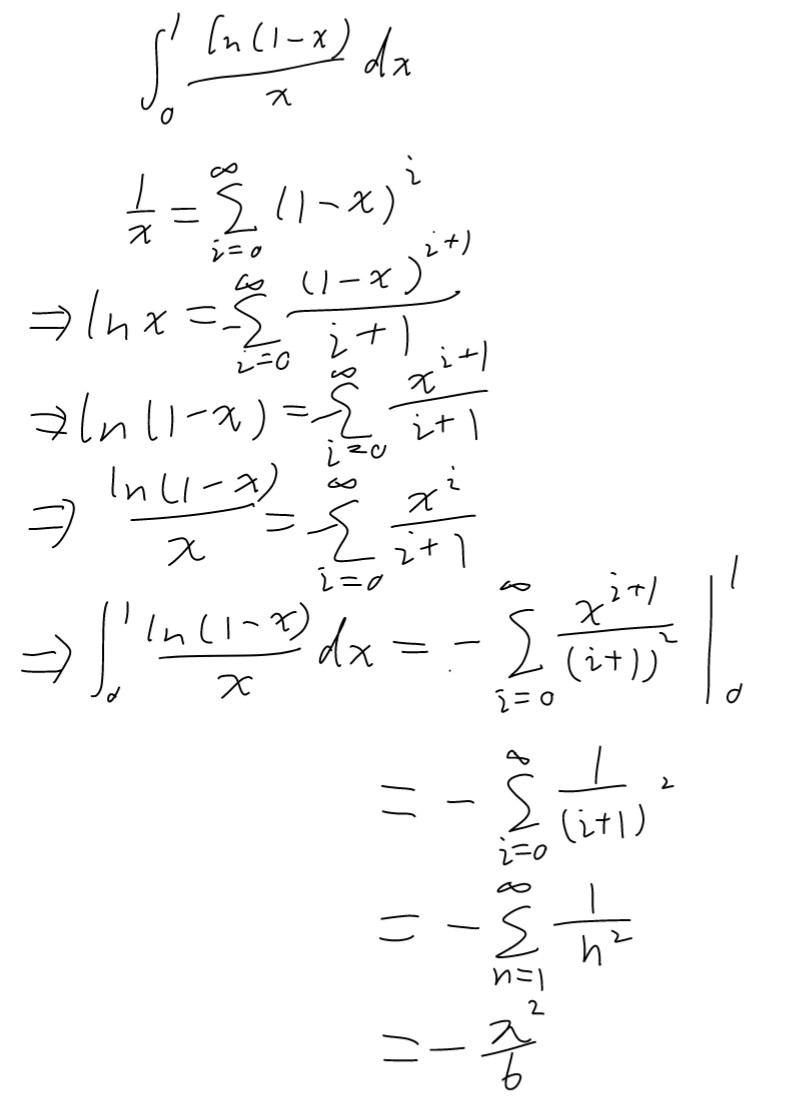物理 [论坛资料室]一个好玩的数学问题
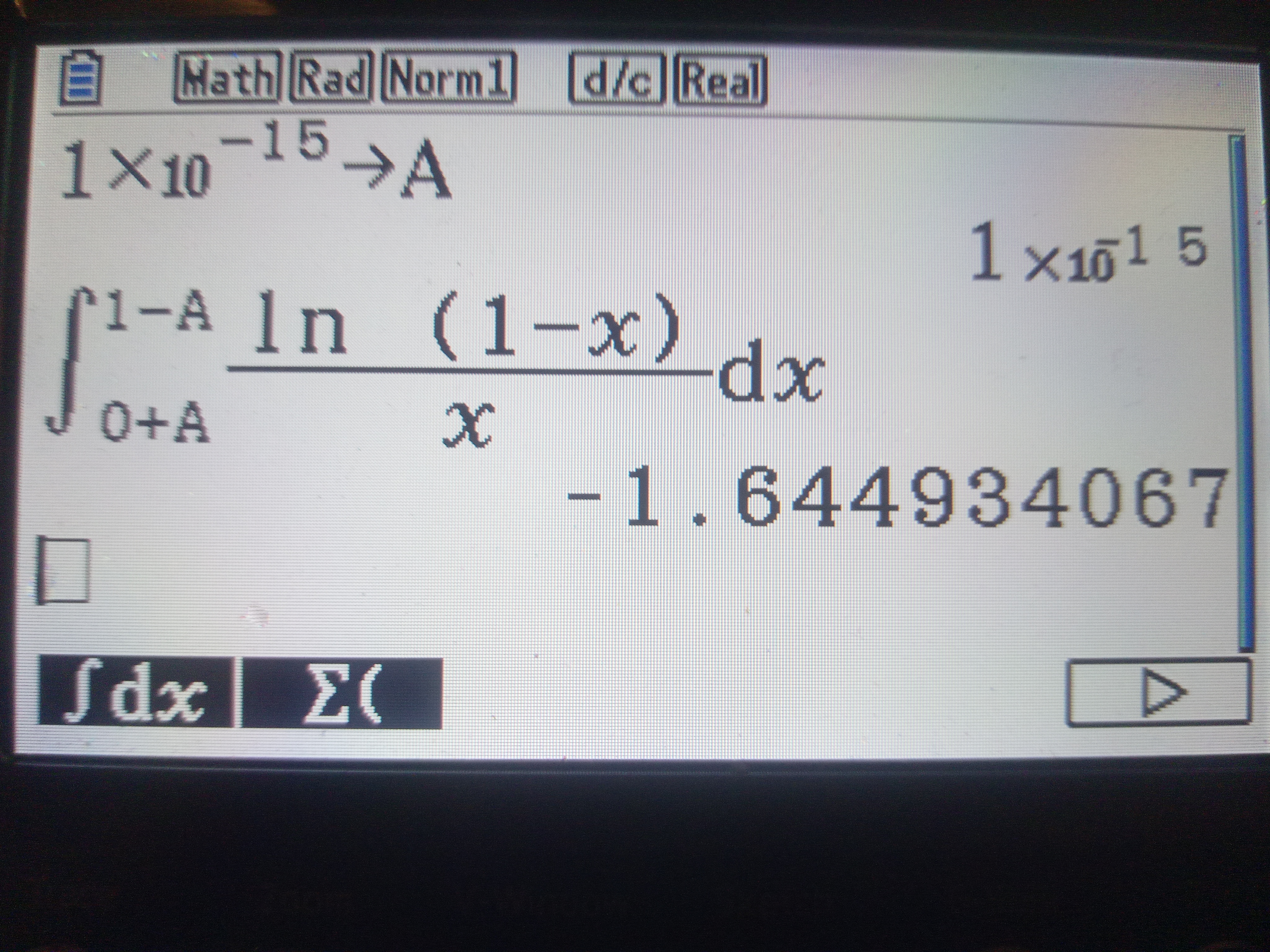
先来问个问题,有没有人知道$\int^0_1\frac{ln(1-x)}{x}$怎么手解,求救
$\sum_{来水积分啊}^{朋友们}$
问了半天没结果,先写算了
事情是这样的,我有个朋友想求$\sum_{n=1}^{+\infty}\frac{1}{n^2}$的值是多少。在初生牛犊不怕虎的精神的指引下,他进行了如下推导。
$\sum_{n=1}^{+\infty}\frac{1}{n^2}$
$=\sum_{n=1}^{+\infty}\int^1_0\frac{x^{n-1}}{n}$
$=\int^1_0\sum_{n=1}^{+\infty}\frac{x^{n-1}}{n}$
此处只需集中注意力就可以发现,$\sum_{n=1}^{+\infty}\frac{x^{n-1}}{n}=\frac{1}{x}\sum_{n=1}^{+\infty}\frac{x^n}{n}$
而巧了么,$\sum_{n=1}^{+\infty}\frac{x^n}{n}$这坨玩意正好是$-ln(1-x)$的泰勒展开!
于是乎
$\sum_{n=1}^{+\infty}\frac{1}{n^2}=\int^0_1\frac{ln(1-x)}{x}$就这么水灵灵的出来了
但问题在于,这个定积分我暂时解不来![]()
于是我去询问了我的老师,他翻阅了高数书,找到了另外一种方法。但鉴于那种方法过于抽象,等我先消化一下再发上来
共6条回复
时间正序