物理 [论坛资料室]闲证定理——三角函数和差角,二倍角,半角公式(新手轮小菜都看得懂)
最近没活整了,回归资料室吧!
我初一一个被用来考数学的无聊的晚自习,提前很久做完了卷子,没有事干,就想起了最近看到的一个公式:余弦和角公式
$\cos(\alpha +\beta)=\cos\alpha\cos\beta -\sin\alpha\sin\beta$
我当时就觉得非常神奇,特别是把公式反过来看更能体现出数学之美所在,于是就萌生了要自己证一下的想法,于是就有了这个帖子
这是一种与教科书完全不同的证明方法,希望能对你们的数学思维产生一点微不足道的帮助
(本文的证明思路,完全是我初一时本人所想,无抄袭现象,若有不严谨之处,请佬们指出)
首先是构造图形,我当时想到了这么个图形
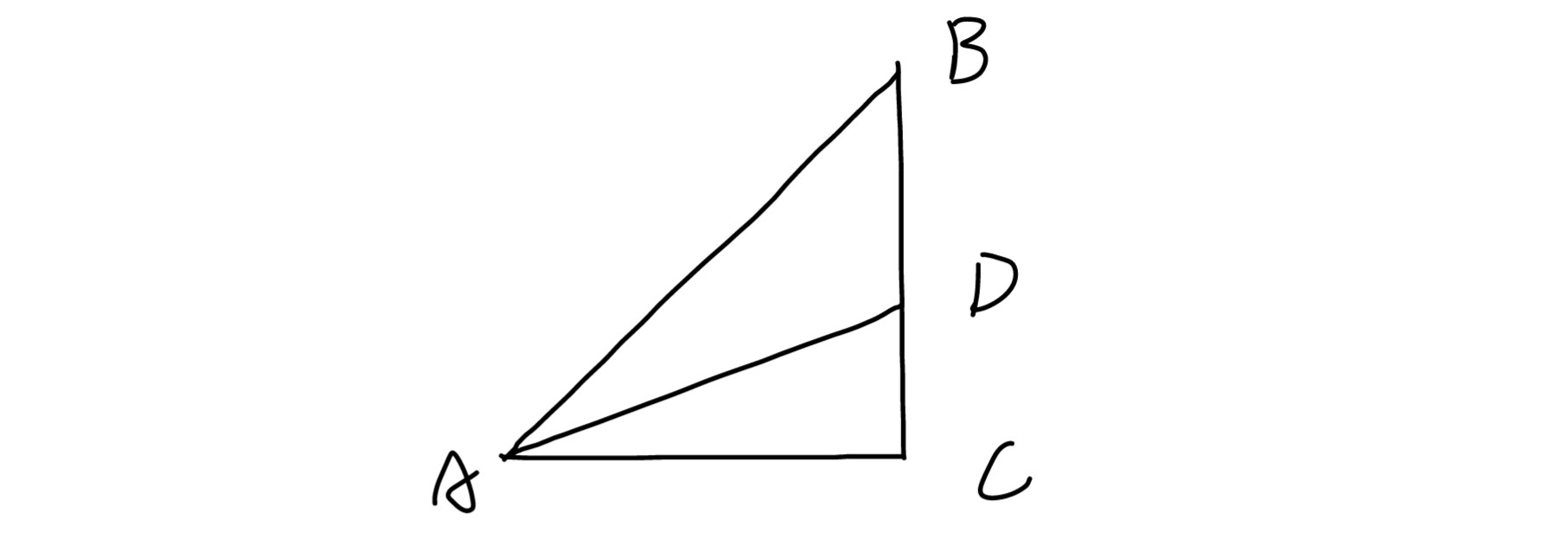
$其中\angle C=90^\circ ,AB=1,D在BC上,\angle CAD=\alpha ,\angle BAD=\beta$
$所以AC=\cos (\alpha +\beta),接下来就只要再找到一种表示AC的方式就能推导出余弦和角公式了$
$我们可以注意到,AC与AD关系密切,有AC=AD\cos\alpha ,所以只要找到一种方法表示AD就能推导出来$
$这个时候我们发现,\beta 还没有派上多大用场,而我们又注意到\cos\beta 与AD的关系密切,只要延长AD至E使得\angle BED=90^\circ ,就能发现这种关系,添完辅助线的图如下$
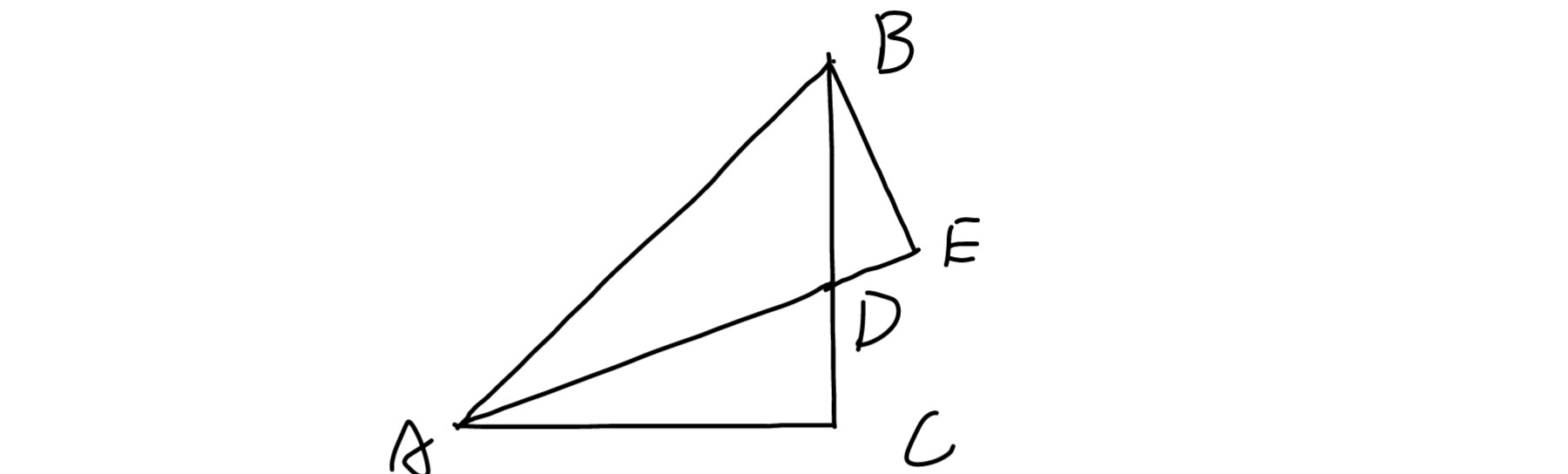
$此时AE=\cos\beta ,我们就只要再找到一种表示DE的方式,就能推出AD,进而推出定理$
$我们注意到,\angle DBE=\alpha ,BE=\sin\beta ,所以DE=BE\tan\alpha=\tan\alpha\sin\beta$
$所以AD=AE-DE=\cos\beta-\tan\alpha\sin\beta ,所以AC=AD\cos\alpha=\cos\alpha(\cos\beta-\tan\alpha\sin\beta)=\cos\alpha\cos\beta -\sin\alpha\sin\beta ,所以\cos(\alpha +\beta)=\cos\alpha\cos\beta -\sin\alpha\sin\beta$
我们的余弦和角公式就这么水灵灵地推出来了
共11条回复
时间正序