希望各位给出更多见解

不是那个无敌的欧拉欧拉欧拉欧拉欧拉欧拉欧拉欧拉欧拉，是

很简洁，是不是，看看证明

我就问你看没看的懂吧，反正我都没学到那

好吧，废话不多说，上车

先从0和1开始

0：无，没有，起点

1：数学里最基本的单位

每一个文明建立一套数学体系，这是最重要的，从0开始，不断的加单位，就可以得到整个自然数集，最自然，最原始。

咱可以用数轴表示这种结构，往右不断增加，而往左是不断减小，所有经典的四则运算都是在此基础上进行

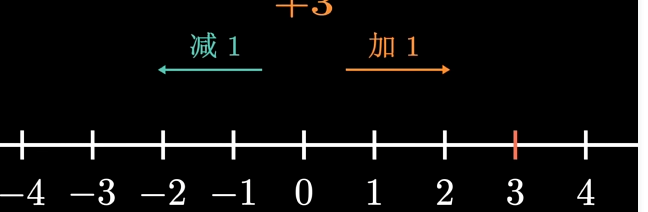
说说虚数单位i吧 

ps:课本上定义是这样的i²=-1，而非i=√-1，很好避免了根号下的数要大于等于0的定义域，但以后√-1记号是很多甚至官方的

相信学到高中的同学想问，为什么两个复数相乘是模长相乘，辐角相加，为什么i有如此神奇的魔力

第一，模长相乘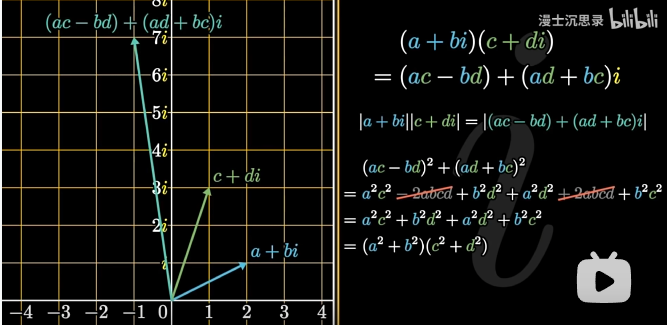

通过小学二年级的计算，得出确实是这样 

ps：这个等式是拉格朗日恒等式，我也不会，如果只考虑实数的部分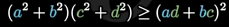柯西不等式

第二，看看辐角

这是复数的三角表示方式，基本都学过吧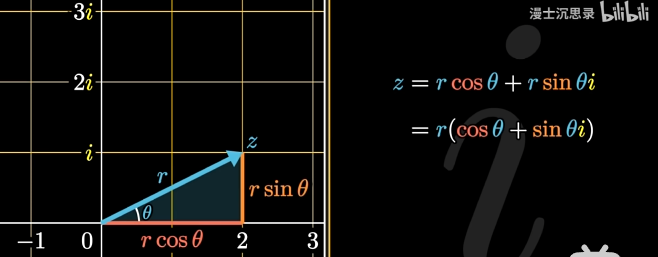

ps：虽然长得像欧拉，其实现在还没他啥事

两个复数一乘，再用三角和差公式一算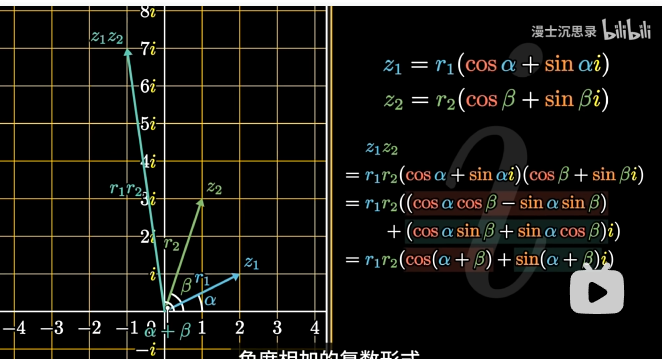

以上的都是lg教过的，但是，为啥就这么巧捏？

其实因果是颠倒，是复数的美丽性质，带来的这样的巧和，这个的巧合的原因，就来源于i²=-1

先看看一个虚数u=a+bi，你是怎么再复平面上找到他的？，先从原点出发，往x实轴方向前进a，再往y虚轴前进b

你再将这个虚数乘i，即iu=-b+ai,你再找找iu

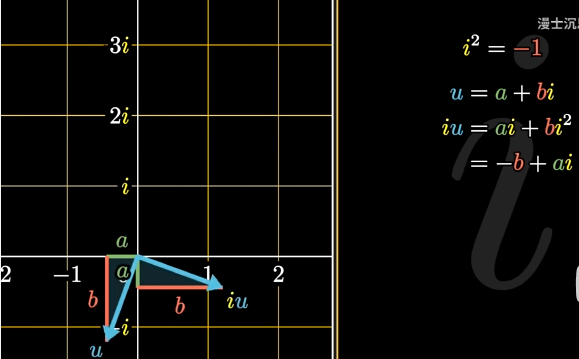
一个明显的旋转全等关系，逆时针旋转90°，无论是哪一个复数

正是因为i的定义，而铸造了这种关系

这下再考虑两个复数相乘的关系，建立一个新坐标系，他的横坐标方向是u，纵就是iu，称为u坐标系

为啥呢，因为这u坐标系也符合复平面的一个性质，任何一个复数x+yi乘了u，可以分别分解成x*u+yi*u

恰恰对应左边u坐标系横坐标前进x，纵坐标前进y的特性，因垂死听啊，所以，这个复数乘上u在复平面上的样子，恰好是这个复数在u平面的样子

ps：已经有包含线性映射，基底，旋转矩阵的思想，线代的思想，当然，我都不会

所以，这个乘积的辐角刚好是这个复数的辐角+u的辐角

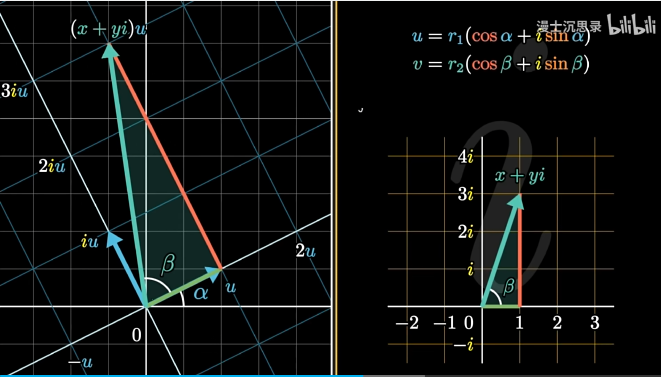
甚至可以用次反推和差角公式，very因垂死听，太优雅的

这些，全来自于i²=-1，

我们不是定义了i，而是i一直都在那，在一个一维的数轴上，原来一直有一个i，这是这个世界，早就蕴含的规律，虚数，他不虚

终于聊完了i，该到他了，e

e有好多定义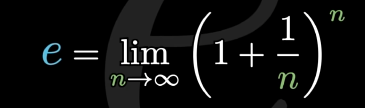

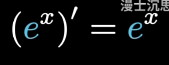
其实最初e来自于复利率，比如，你存入了1元，他一年过后会变为2元

如果，在一年内，你存取n次，就是每过1/n年，你就取出利润的钱，然后当做本金存回去

那么，每次存取，你的钱会变成你的(1+1/n)倍，最终你的钱会变为(1+1/n)ⁿ

贪婪的商人发现，就算n趋近无穷，也只会收敛到一个有限的值，≈2.71828，这就是e无穷极限的定义方式

其实在这个定义里，已经蕴含着e的x次方的倒数也是他本身

这下，要解决一个核心意味e^ix到底意味着什么，为什么在π的函数值变为-1

你将e^ix求导，ie^ix，也就差个i倍，在复平面上说过，乘i，就是逆时针旋转90°

其实，e^ix描绘了一个二维向量在复平面上的运动过程，初始时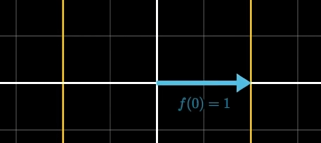

之后每个时刻，他位置的导数，也就是运动的速度，都是位置向量乘了i，他的速度永远垂直于原点

这下，学过高中物理的人要因垂死听了，这是啥，和洛伦兹力一样，圆周运动啊

运用i构建的几何特性，和e导数等于自身的特质，e^ix，是一个从1，0开始，沿着单位圆的运动轨迹，x，便代表了你前进长度为x的圆弧

再结合一点三角函数，这下，终于出来了，欧拉公式，本质，就是把单位圆上的点，用三角分解的性质表现出来

最后，再带入π，最美丽的公式出来了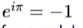

欧拉公式，是运用了i的几何特性，e的自导特性，π的定义，构建了这个美丽的公式，0，1，e，π，i，被欧拉用一个公式，解决了

这就是，数学的美

转载于

【漫士科普】如何最简单且本质地理解欧拉公式？

漫士沉思录

cc协议