数学

[代数专题]因式分解

     [2024年10月2日已更新]

因式分解是代数的基础，无论是在中考还是竞赛，重要性都不言而喻，接下来我将带你掌握因式分解这个实用的工具

      1.因式分解的定义

        把一个多项式化成几个整式的积的形式，这种变形叫做因式分解(因式分解也可称为分解因式)

      2.因式分解的实质

        是一种和化为积的恒等变形(因式分解和整式乘法互为逆运算)

      3.因式分解的注意事项

         ①必须是恒等变形

         ②必须把结果写成整式乘积的形式

         ③必须分解彻底，即分解到每个多项式都不能再分解为止

      4.因式分解的方法

       因式分解总共有十个方法。         这里划一个重点！！

      №1.提公因式法

         [1]公因式：多项式各项都含有的相同因式，叫做这个多项式各项的公因式

         [2]提公因式法:如果一个多项式的各项都含有公因式，那么就可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式。

                例如：ab+ac+ad=a(b+c+d)

          [3]注意事项

          (1)公因式要提尽，不要有所遗漏

          (2)因式分解的结果，一般要先写单项式，再写多项式，相同的因式写成幂的形式

          (3)在将公因式提到括号外时，一般将括号内多项式的首项系数变为正数[eg.-ab+bc-bd=-b(a-c+d)]

          №2.公式法

             [1]公式法:如果把乘法公式反过来，就可以把某些多项式因式分解，这种方法称为公式法

                 例如:$a^2-1^2=(a+1)(a-1)$

               ✨常用公式：

                 ①平方差公式：$a^2-b^2=(a+b)(a-b)$

                 ②完全平方公式：$a^2±2ab+b^2=(a±b)^2$

                 ③三项乘法公式：$a^2+b^2+c^2+2ab+2bc+2ac=(a+b+c)^2$；$2a^2+2b^2+2c^2+2ab+2bc+2ac=(a+b)^2+(b+c)^2+(a+c)^2$

                 ④ 立方和公式：$a^3+b^3=(a+b)(a^2-ab+b^2)$

                 ⑤ 立方差公式：$a^3-b^3=(a-b)(a^2+ab+b^2)$

                 ⑥和的立方公式：$a^3+3a^2b+3ab^2+b^3=(a+b)^3$

                 ⑦差的立方公式：$a^3-3a^2b+3ab^2-b^3=(a-b)^3$

                 ⑧三个老头公式：$a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ac)$

   ♣以上公式可以根据情况进行合理使用。

             №3.分组分解法

                [1]分组分解法:对于有些题目，恰当分组是关键。能分组分解的多项式一般为四到六项(也有特殊情况)，在分组时要有'可持续发展’的眼光，进行合适的分组，使得分组之后可以运用提公因式法和公式法。

               例如:ma+mb+na+nb=(ma+mb)+(na+nb)=m(a+b)+n(a+b)=(a+b)(m+n)

              №4.十字相乘法

               [1]十字相乘法：对形如$Ax^2+Bx+C$的二次三项式，我们常常可以用十字相乘法来因式分解。

                        分解二次三项式$Ax^2+Bx+C$，把A拆为A1，A2，C拆为C1，C2，且A1×A2=A，C1×C2=C.

                       A1                            C1                    若满足：A1×C2+A2×C1=B

                                                                                 则：原式=(A1x+C1)(A2x+C2)

                       A2                            C2

              如果不理解，请看下图

例如：$x^2+3x+2=(x+1)(x+2)$

            x           1

           x           2

      №5.双十字相乘法

        [1]双十字相乘法: 对形如$Ax^2+Bxy+Cy^2+Dx+Ey+F$的二元二次六项式，我们常常可以用双十字相乘法。(双十字相乘法的主要思路就是多次利用十字相乘法)

     分解二元二次六项式$Ax^2+Bxy+Cy^2+Dx+Ey+F$，将A分解成a1，a2乘积作为一列，C分解成c1，c2乘积作为一列，F分解成f1，f2乘积作为一列

                                              a1             c1                     f1       若a1c2+a2c1=B，c1f2+c2f1=E，a1f2+a2f1=D(也就是第1，2列、第2,3列、第1,3列都满足十字相乘规则)

                                                                                                    则原式=(a1x+c1y+f1)(a2x+c2y+f2)

                                              a2             c2                     f2

      如果不理解，请看下图

  例如：$x^2+2xy-3y^2+3x+y+2=(x-y+1)(x+3y+2)$              $x^2-4xy+3y^2-6y-9=x^2-4xy+3y^2-6y-9+0x=(x-y+3)(x-3y-3)$

                x          -y               +1                                                                                            x            -y           +3

               x         +3y            +2                                                                                             x             -3y        -3       

         №6.主元法

           [1]主元法:当遇到多元多次多项式时，我们可以把其中一个未知数看作主要未知数(称为‘主元’)，其余未知数当成参数，按主元作降幂整理，再用其他因式分解技巧进行分解

          ❄大致步骤：(1)选一个字母作为未知数(主元)，其余作为常数(！！尽量选择次数较低的字母作为主元)

                                   (2)按所选字母降幂排列，合并同类项

                                   (3)运用因式分解技巧分解因式

       例如：1+a+b+c+ab+ac+bc+abc=(a+ab+ac+abc)+(1+b+c+bc)=(a+1)(1+b+c+bc)=（a+1)(b+1)(c+1)

                                                             ↑选定a为主元

                 №7.换元法

                [1]换元法:对于复杂的代数式，将其中相同的部分看成一个整体，用一个新的变量(字母)代替，从而简化代数式，然后进行因式分解，最后将原代数式代入。

                  例如：$(x^2+4x+2)(x^2+4x+6)+4$                                                          x(x+1)(x+2)(x+3)+1

                   解：不妨设$x^2+4x+2=a$，$x^2+4x+6=a+4 $                        解：原式=[x(x+3)][(x+1)(x+2)]+1

                       原式=a(a+4)+4                                                                                          =$(x^2+3x)(x^2+3x+2)+1$        

                               =$a^2+4a+4$                                                                          不妨设$x^2+3x=a$，$x^2+3x+2=a+2$

                               =$(a+2)^2$                                                                               原式=a(a+2)+1

                               =$(x^2+4x+4)^2$                                                                            =$a^2+2a+1$

                              =$(x+2)^4$                                                                                       =$(a+1)^2$

                                                                                                                                         =$(x^2+3x+1)^2$

                           №8.拆添项法

                            [1]拆添项法:对于有些代数式，不能直接分解并且也没有明显可以换元的项，这时可以尝试将其中的某一项拆成两项或者添加一些特殊的项起到‘桥梁’的作用，然后再用常用方法来因式分解

                             [2]分类：

                              ①系数相关型❨拆❩：按照某个字母降幂排列，观察代数式中项与系数的绝对值，若其中几项与几项系数的绝对值相等，则可以通过拆项和适当分组来因式分解。(！！！一般来说，拆的是系数高的项或者是中间项，然后系数相同的部分分一组进行因式分解)

             例如：$x^3$+$6x^2$+11x+6

                解：原式=($x^3$+$x^2$)+($5x^2$+5x)+(6x+6)

                                =$x^2$(x+1)+5x(x+1)+6(x+1)

                                =(x+1)($x^2$+5x+6)

                                =(x+1)(x+2)(x+3)

                    ②公式相关型(添)：如果代数式结构与前面学过的公式类似，但用公式直接分解则缺项，这时需要通过添项凑成公式的结构再进行因式分解(!!添项时需要加上仅符号相反的两项)

                          例如：$a^4$+4

                解：原式=($a^4$+$4a^2$+4)$-4a^2$

                               =($a^2$+2)-$(2a)^2$

                               =($a^2$+2+2a)($a^2$+2-2a)

                   №9.因式定理

                      [1]因式定理:如果x=a时，多项式$a_nx^n+a_{n-1}x^{n-1}+…+a_1x+a_0$的值为0，那么x-a是该多项式的一个因式

                      [2]实质:有理根(如图所示)

                    [3]一般步骤：

                     ①求出能使多项式值为0的有理根x=a

                     ②表示出多项式的一个因式(x-a)

                      ③利用大除法将多项式除以(x-a)，得到多项式的另一个因式。(也可以用待定系数法)

                         (！！注意：另一个因式有时候还能继续分解，一定要分解彻底！)

                  例如：(如图所示)

        №10.待定系数法

           [1]待定系数法:先设含有待定系数的表达式，再根据条件确定系数，从而得出所求表达式。

           [2]大致步骤:①分析多项式特征：观察待因式分解的多项式，确定其次数、各项系数的特点以及可能的因式形式

            ②设出因式形式：根据多项式的特征，设出含有待定系数的因式表达式。[比如对于二次三项式，可设为(ax+b)(cx+d)的形式]

            ③展开式子：将设出的含有待定系数的因式表达式展开[比如$acx^2+bcx+abx+bd$]

            ④对比系数：把展开后的多项式与原式进行对比，根据对应项的系数相等，列出关于待定系数的方程组

            ⑤求解系数：解方程组，求出待定系数的值

            ⑥写出因式分解结果：将求出的待定系数代入所设的因式表达式中，从而得到原式的因式分解结果

            [3]例如:如图所示

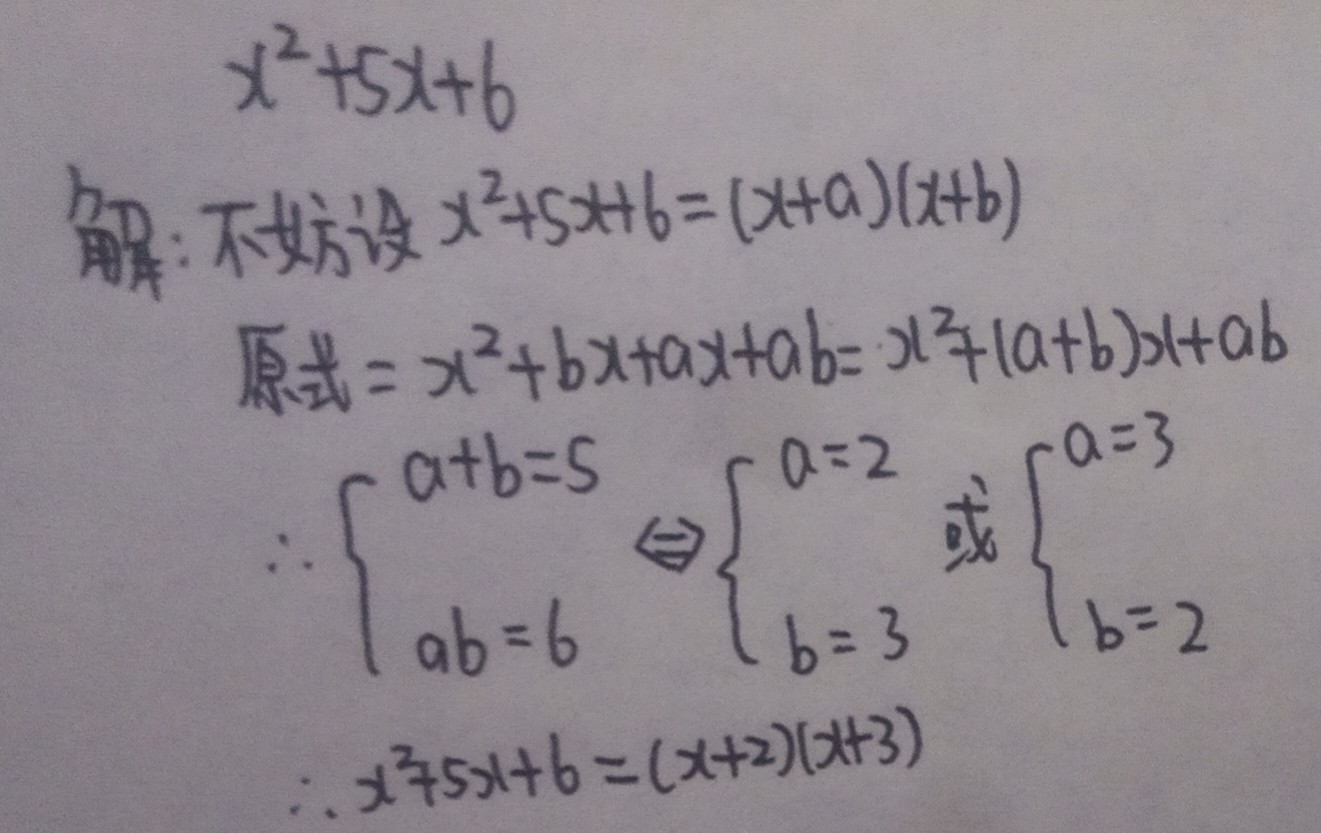
       以上就是因式分解的全部内容啦😋，如果有遗漏，请从评论区里指出来哦！

        备注：因式分解推荐书目：1.小蓝本———因式分解技巧  2.培优新方法