- 时间正序
- 时间倒序
- 评论最多
这不就是把三类基本行(列)变换放到分块矩阵上来了吗。。。
只要把每一个矩阵看成是一个数字,再按照理解三类基本行(列)变换的方式来理解不就好了吗。。。
你别告诉我你连三类基本行(列)变换都理解不了()
- 1
$由于 V_{\lambda_0} 是 V 的子空间,选择一个基 \{ \mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_k \} ,其中 k 是 V_{\lambda_0} 的维数然后对于基中的每个向量 \mathbf{v}_i ,计算 A\mathbf{v}_i 。由于 \mathbf{v}_i 是对应于 \lambda_0 的特征向量,有 A\mathbf{v}_i = \lambda_0 \mathbf{v}_i
表示矩阵 [A|_{V_{\lambda_0}}] 是一个 k \times k 矩阵,其中第 i 列是 A\mathbf{v}_i 在基 \{ \mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_k \} 下的坐标向量。由于 A\mathbf{v}_i = \lambda_0 \mathbf{v}_i ,矩阵 [A|_{V_{\lambda_0}}] 的每一列都是 \lambda_0 乘以基向量的坐标向量。因此,矩阵 [A|_{V_{\lambda_0}}] 是一个对角线上有 \lambda_0 的对角矩阵$
瞎写的,错了别找我
这公式有点逆天了,重新再发一遍
$特征子空间 V_{\lambda_0} 是所有对应于特征值 \lambda_0 的特征向量以及零向量的集合$
$由于 V_{\lambda_0} 是 V 的子空间,选择一个基 \{ \mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_k \} $,
$其中 k 是 V_{\lambda_0} 的维数$
$对于基中的每个向量 \mathbf{v}_i ,计算
A\mathbf{v}_i 。由于 \mathbf{v}_i 是对应于 \lambda_0 的特征向量,我们有 $
$A\mathbf{v}_i = \lambda_0 \mathbf{v}_i 。
$ 表示矩阵 [A|_{V_{\lambda_0}}] 是一个 k \times k 矩阵,其中第 i 列是 A\mathbf{v}_i 在基 \{ \mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_k \} 下的坐标向量。$
$由于 A\mathbf{v}_i = \lambda_0 \mathbf{v}_i ,矩阵 [A|_{V_{\lambda_0}}] 的每一列都是 \lambda_0 乘以基向量的坐标向量。因此,矩阵 [A|_{V_{\lambda_0}}] 是一个对角线上有 \lambda_0 的对角矩阵$
计算$$I=\int_{0}^{\frac{\pi}{2}}\ln\sin x~\mathrm{d}x$$
换元,令$u=\dfrac{\pi}{2}-x$,则原积分变为
$$\begin{aligned}I&=\int_{0}^{\frac{\pi}{2}}\ln\sin x~\mathrm{d}x\\&=\int_{\frac{\pi}{2}}^{0}\ln\sin \left(\dfrac{\pi}{2}-u\right)~\mathrm{d}\left(\dfrac{\pi}{2}-u\right)\\&=\int_{0}^{\frac{\pi}{2}}\ln\cos u~\mathrm{d}u\end{aligned}$$
则
$$\begin{aligned}2I&=\int_{0}^{\frac{\pi}{2}}\ln\sin x~\mathrm{d}x+\int_{0}^{\frac{\pi}{2}}\ln\cos x~\mathrm{d}x\\&=\int_{0}^{\frac{\pi}{2}}\ln(\sin x\cos x)\mathrm{d}x\\&=\int_{0}^{\frac{\pi}{2}}\ln\left(\dfrac{1}{2}\times\sin 2x\right)\mathrm{d}x\\&=\int_{0}^{\frac{\pi}{2}}\ln\dfrac{1}{2}\mathrm{d}x+\int_{0}^{\frac{\pi}{2}}\ln\sin 2x~\mathrm{d}x\\&=\dfrac{\pi}{2}\ln\dfrac{1}{2}+\dfrac{1}{2}\int_{0}^{\frac{\pi}{2}}\ln\sin 2x~\mathrm{d}(2x)\\&=-\dfrac{\pi}{2}\ln 2+\dfrac{1}{2}\int_{0}^{\pi}\ln \sin v~\mathrm{d}v\\&=-\dfrac{\pi}{2}\ln 2+\dfrac{1}{2}\left(\int_{0}^{\frac{\pi}{2}}\ln\sin v~\mathrm{d}v+\int_{\frac{\pi}{2}}^{\pi}\ln\sin v~\mathrm{d}v\right)\\&=-\dfrac{\pi}{2}\ln 2+\dfrac{1}{2}\left(\int_{0}^{\frac{\pi}{2}}\ln\sin v~\mathrm{d}v+\int_{\pi-\frac{\pi}{2}}^{\pi-\pi}\ln\sin (\pi-w)~\mathrm{d}(\pi-w)\right)\\&=-\dfrac{\pi}{2}\ln 2+\dfrac{1}{2}\left(\int_{0}^{\frac{\pi}{2}}\ln\sin v~\mathrm{d}v+\int_{\frac{\pi}{2}}^{0}\ln\sin w~\mathrm{d}(-w)\right)\\&=-\dfrac{\pi}{2}\ln 2+\dfrac{1}{2}\left(\int_{0}^{\frac{\pi}{2}}\ln\sin v~\mathrm{d}v+\int_{0}^{\frac{\pi}{2}}\ln\sin w~\mathrm{d}w\right)\\&=-\dfrac{\pi}{2}\ln 2+\dfrac{1}{2}\times2I\\&=-\dfrac{\pi}{2}\ln 2+I\end{aligned}$$
所以
$$I=\int_{0}^{\frac{\pi}{2}}\ln\sin x~\mathrm{d}x=-\dfrac{\pi}{2}\ln 2$$

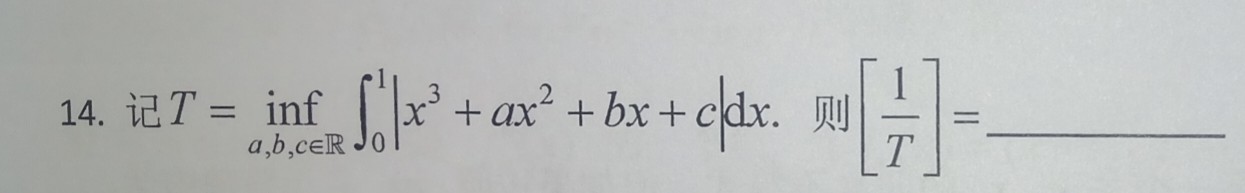
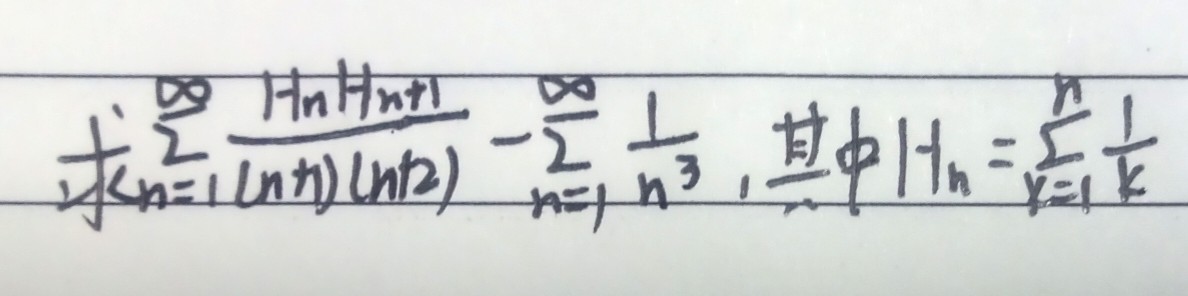
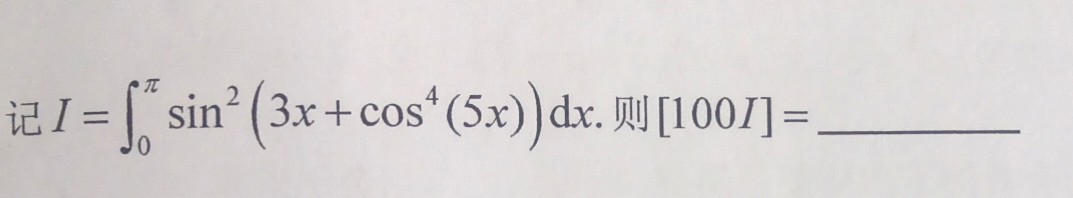 一道积分把我算傻了
一道积分把我算傻了