物理

Demanding的循环帖

＊自创题目

（一）$\text{对于互相平行两面}\alpha_1,\alpha_2\text{，}$ $\text{取 }\alpha_1,\alpha_2\text{ 外围图形为 }S_1,S_2\text{，}$ $\text{建立映射 }f:S_1 \to S_2\text{ 使得：}$

$1. \forall A\in S_1,f(A)\in S_2.$

$2. \forall B\in S_2,\exists A\in S_1,f(A)=B.$

$\text{对于所有 }A\in S_1\text{，}$ $\text{连接 }A\text{ 与 }f(A)\text{ 构成线段 }l_A\text{，}$ $\text{令集合 }L\text{ 为所有上述线段的集合。}$

$\text{令集合 }V=\alpha_1\cup\alpha_2\cup L\text{。}$

$\text{在 }\alpha_1,\alpha_2\text{ 内取基准点 }O_1,O_2\text{。}$ $\text{在 }\alpha_1\text{ 面内，}$ $\text{以 }O_1\text{ 为原点，}$ $\vec{n}\text{ 为 }x\text{ 轴正方向，}$ $\vec{z}\text{ 为 }z\text{ 轴正方向。}$ $\text{在 }xOy\text{ 上，}$ $\text{方程 }g_1(x,y)\text{ 表示 }S_1\text{ 的方程（上述内容满足右手直角坐标系）。}$ $\text{同理，可在 }\alpha_2 \text{ 面上定义 }g_2(x,y)\text{。}$

$\text{现取 }\vec{O_1O_2}\text{ 在 }\alpha_1\text{ 面上投影 }\vec{m}\text{，}$ $\vec{z}\text{ 满足 }\vec{z}\perp\alpha_1\text{，}$ $\vec{z}+\vec{m}=\vec{O_1O_2}\text{。}$

$(1)\text{上述描述中，现要使 }f:S_1 \to S_2 \text{ 满足 }S_1 \text{ 与 }S_2 \text{ 元素一一对应，}$ $ \text{请在已有的两个条件后补充尽可能少的条件。}$

$(2)\text{若使 }V\text{ 为下列几何体的表面，}$ $\text{给出尽可能少的关于题目描述中参量的条件，并指出是否存在无法表达的特例：}$

$(2.1)\text{柱体（如圆柱）；}$ $(2.2)\text{锥体（如圆锥）；}$ $(2.3)\text{台体（如圆台）。}$

$(3)\text{是否所有非上述特例的 }V\text{ 均可用 }O_1,O_2,g_1,g_2,f,\vec{n}\text{ 表示？}$ $\text{若是，请证明；}$ $\text{否则，给出还需要的参量（题目描述中的）并证明。}$

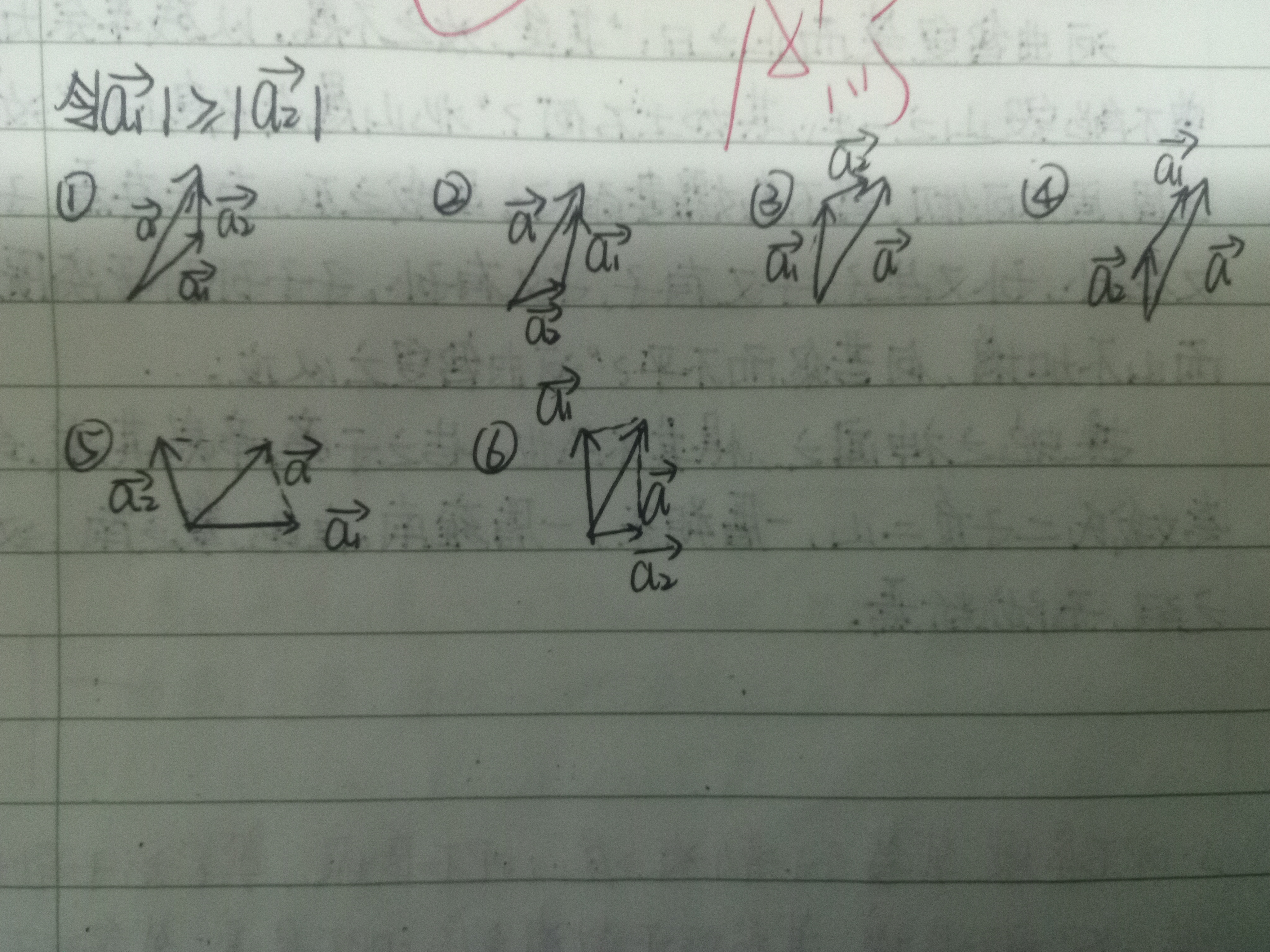
（二）$\text{有 }n\text{ 个向量 }\vec{a_1},\vec{a_2},\cdots,\vec{a_n}\text{，}$ $\text{满足所有向量相加为一个确定的向量 }\vec{a}\text{。}$ $\text{ 向量 }\vec{a_i}\text{ 的大小为 }t_i\text{，是定值，}$ $\text{则：}$

$(1)\text{当 }n = 2\text{，有多少个可能的向量对 }(\vec{a_1},\vec{a_2})\text{。}$

$(2)\text{设向量 }\vec{b_i}=\sum\limits_{j=1}^{i}\vec{a_j}\text{，则：}$

$(2.1)\text{当 }n = 4\text{，}\text{求 }\lvert\vec{b_1}\vert+\lvert\vec{b_2}\vert+\lvert\vec{b_3}\vert+\lvert\vec{b_4}\vert\text{ 的取值范围；}$

$(2.2)\text{当 }n\text{ 为任意正整数，求 }\sum\limits_{i=1}^{n}\lvert\vec{b_i}\vert\text{ 和 }\lvert\sum\limits_{i=1}^{n}\vec{b_i}\vert\text{ 的取值范围。}$

* $(2)\text{ 的题目答案均用 }t_i,\vec{a}\text{ 表示。}$

（三）$\text{对于首项为 }1\text{，}$ $\text{公比为 }t (t$>$1)\text{，}$ $\text{项数为 }a\text{ 的等比数列 }A_n\text{，}$ $\text{正整数 }b\text{ 使得在数列 }A_n\text{ 中取 }b\text{ 项元素可以重新组成一个项数为 }b\text{ 的等差数列，}$ $\text{则称数对 }(t,a,b)\text{ 是“热情”的。}$

$(1)\text{对于任意“热情”的数对 }(t,a,b)\text{，试证：}2a\geq b^2-b+2。$

$(2)\text{对于“热情”的数对 }(t,a,b)\text{，当 }a\to+\infty\text{，试证： }b\not\to+\infty\text{。}$

$(3)\text{利用题目背景和上述结论，试证：实数集的大小大于整数集的大小。}$

（四）$\text{现有一个圆锥 A-S，其中 A 为顶点、S 为圆锥底面， O 为底面圆心， B 为底面圆上一点， C、D 为圆锥侧面上的点，圆锥母线长 }d\text{，}$ $\text{底面半径为}r\text{。}$

$\text{有点 P 位于侧面上，其运动轨迹如图所示，特别的，其运动过程中会在 K 点处与底面重合，并且运动一周过程中其会重复经过 Q 点两次。}$

现定义：

$1.\text{侧面上任一点 N 到顶点 A 的直线距离称为点N的“顶距”，记为 }\text{top}(N)\text{；}$

$2.\text{过侧面上任一点 N 做平面 }\alpha\text{ 使 }\alpha\text{ 平行于底面 S，取 }\alpha\text{ 与圆锥表面的交线 S'，易知 S' 为一个圆，取 S' 与直线 AB 的交点为 U。现使点 N' 从 N 点开始逆时针沿圆 S' 运动至 U，}$ $\text{N' 运动路径的长度称为点 N 的“围长”，记为 }\text{cir}(U)\text{；}$

$3.\text{记侧面上任一点 N 的“角度”为 }\text{rad}(N)\text{，其满足 }\text{rad}(N)=\frac{\text{cir}(N)}{\text{top}(N)}\text{；}$

$4.\text{记侧面上任两点 M,N 的“距离”为 }\text{dis}(M,N)\text{，其满足 }\text{dis}(M,N)=\sqrt{\text{top}^2(M)+\text{top}^2(N)-2\cdot \text{top}(M)\cdot\text{top}(N)\cos(|\text{rad}(M)-\text{rad}(N)|)}\text{。}$

现已知：

$1.\text{直线 CD 平行于底面 S 且垂直于直线 AB；}$

$2.d=3r\text{；}$

$3.\text{dis}(P,C)+\text{dis}(P,D)=2\sqrt{3}\text{；}$

$4.\text{dis}(D,Q)=2\cdot\text{dis}(C,Q)\text{。}$

试求：$\text{圆锥 A-S 的体积}V\text{。}$

＊自我介绍

地点：HB WH

性别：男

年龄：15，初三

竞赛：现物理，曾信息、数学

喜好：mc以及历史、数学、物理学科

讨厌：道法、地理、体育学科（体育中考考完了，终于不用折磨自己了）