数学

三角函数;

高中:弧长制(rad) π＝180°;

常用公式:

1诱导公式:共54个,9组;前五组为同名诱导公式,后四组为不同名诱导公式;[口令:奇变偶不变,符号看象限]

2正弦公式:sin(α±β)=sinαcosβ±sinβcosα;

3正切公式:tan(α±β)=(tanα干tanβ)/(1±tanαtanβ);

4:二被角公式:sin2α=2sinαcosα;

反三角函数:单调函数必有反函数,而三角函数不是单调函数[所以反三角函数[正弦]的表达式是 y=arcsinx=$sin^-1$x.

图像如图一;

arcsinx=y y∈[－π/2,π/2]-------------------------角

sin(arcsinx)=x,x∈[-1,1]----------------------------值

问:cos(arcsinx)=?

sin(arcsinx)=x;先前定义arcsinx＝y

所以sin(y)=x;cos(y)=$sqrt(1-x^2)$.

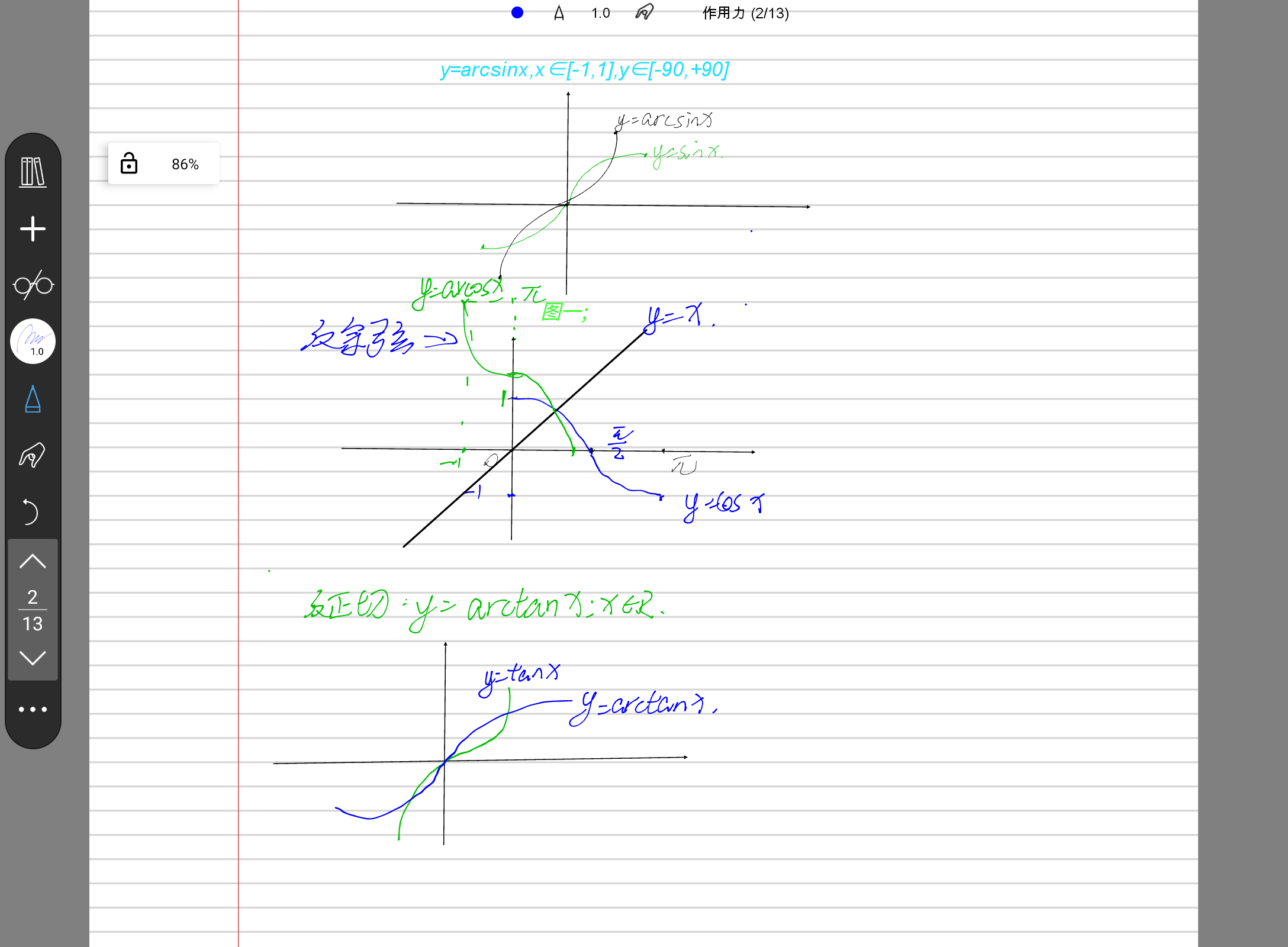
补充:已知tanarctanx=x;

设arctanx=y;

问sin(y)或cos(y)的值?

解:画三角形

如下图做三角形即可.

可得到答案;[arcsin相当于位移，则这里是求导，微积分]

四:三角方程:

sin x=a 1:|a|>1:$∅$

        2:|a|=1:${x|x=2kπ+arcsin a,k∈Z}$

              3:|a|<1:${x|x=kπ+((-1)^k)*arcsin a,k∈Z}$

cos x=a 1:|a|>1:$∅$

        2:|a|=1:${x|x=2kπ+arccos a,k∈Z}$

              3:|a|<1:${x|x=kπ+((-1)^k)*arccos a,k∈Z}$

tan x=a(a∈R):${x|x=kπ+arctan a,k∈Z}$

衔接内容结束,可回归数学新手轮1~10复习资料