物理 [论坛资料室]映射:世界的影子
“映射,让我们看到世界的影子。”
——某不知名数学家
映射,这个名词我们都不陌生。它不算难,但却在数学中占据重要的地位。而我们今天的主题——对于空间的变换,也就是投射空间的影子,就要运用映射的概念。
首先讲一个最最基础的概念,集合。所谓集合就是一堆有共同特征的元素放在一起,可以是数字,矩阵,函数,向量,张量,代数对象,几何对象,甚至是你中午吃的菜,都可以是这样的元素。总之就是一些有共同特征的东西堆在一起,这就是集合。下面给出一些常用集合,它们在今天的讨论中至关重要。

不过这里要注意的一点是,集合上增加一个指数,说明这个集合中的元素是由指数个“底数”集合中的指数个元素组成的,比如实n维线性空间,就是在n个实数集中选取n个数,来表征实n维线性空间中的一个元素。
此外,集合的几何意义就是空间。换句话说,每一个集合都对标了一个空间。比如实数集其实对应了一条数轴,也就是一个一维空间。之后我们会讲到,复数集等价于实2维线性空间,所以复数集代表了复平面。
接下来可以请出我们今天的主角了。所谓映射,包含三个必要元素,即原空间,像空间和对应关系。我们选择一个对应关系,将原空间(一个集合)中的每一个元素对应到像空间(另一个集合)中的元素上。一般情况下,任意映射可以用下面这两个式子表达:
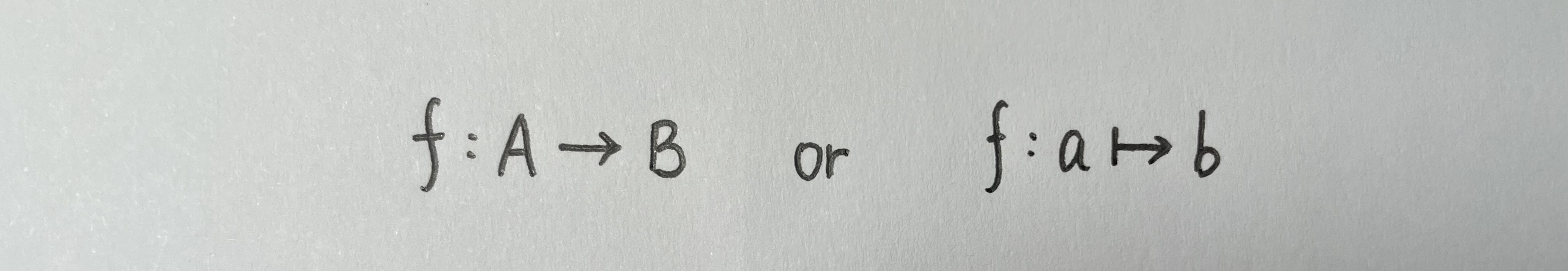
其中f是一个对应关系,A,B是集合,a,b分别是这两个集合中的元素。这个f,我们给它起个名字,就是函数。
举个例子,函数y=x+1,很明显,它是这样一个映射:
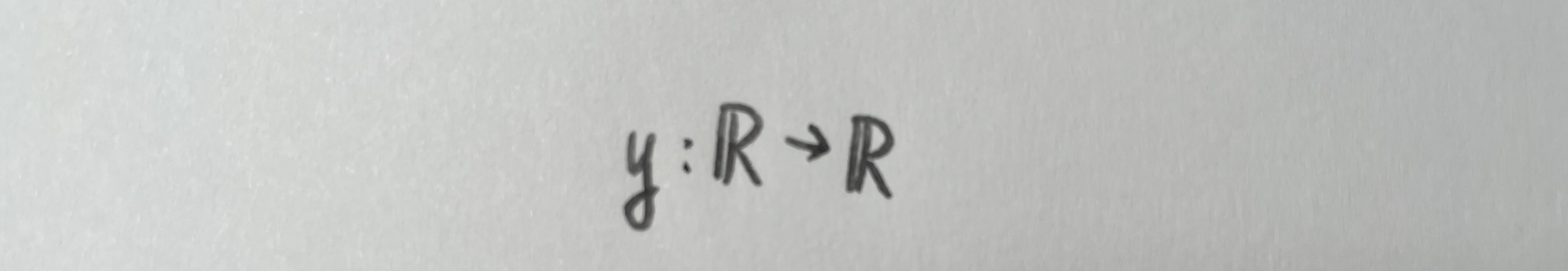
它是一个一维空间到一维空间的映射。这不难理解。你也可以认为,这个函数把一条直线映射为了一条直线。同样的,非线性函数就会把这条直线扭曲成曲线,这就是我们说的,空间的映射,空间的影子。同理,我们可以列出一些别的映射:
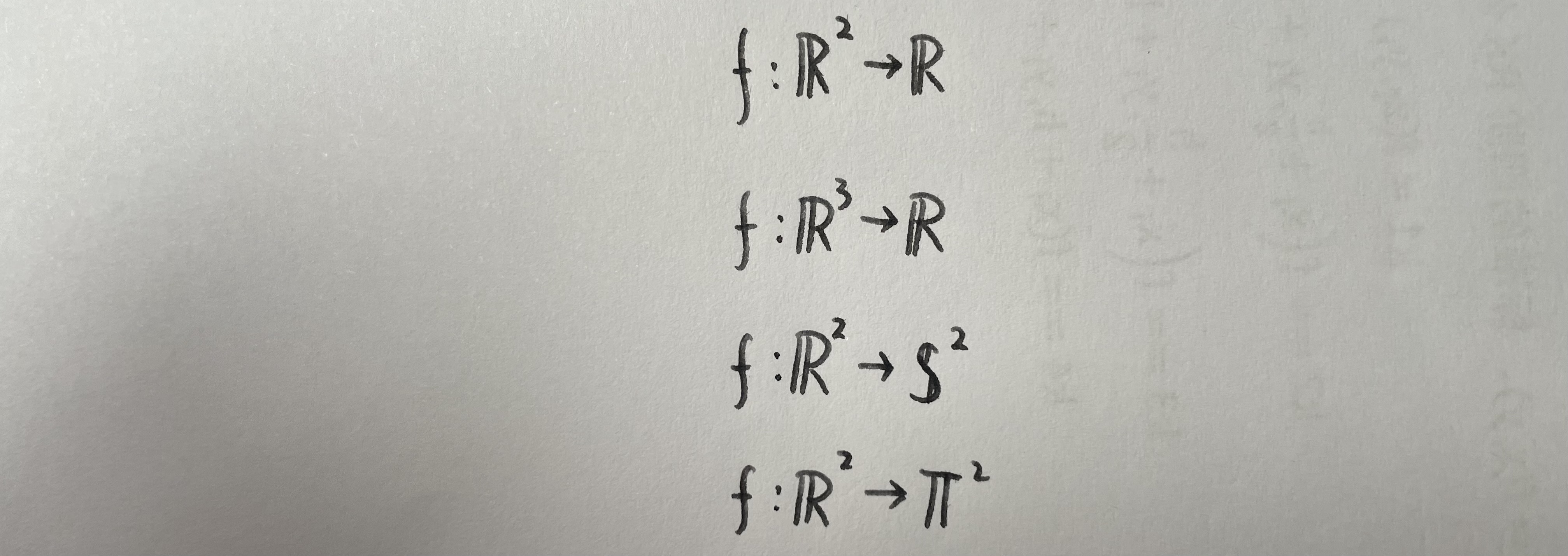
第一个映射把一张平面扭曲成曲面,第二个映射就是物理学中的场,它赋予空间中每一点一个值,当然你也可以把它理解为是三维空间的扭曲,只不过这个扭曲需要在更高维度的空间中表征。第三个第四个映射分别把二维空间扭曲成球面和环面。如果你在这里已经感觉晕了,那么从头再翻一遍。如果你感觉良好,那我们继续。
假设你是一个生活在一维世界中的数学家,你现在发现了最简单的函数y=2x,你想把它表示出来。很明显我们在二维中构造x轴和y轴的方法行不通了,我们只能尝试变换坐标线。哦不,在一维空间中,它应该叫做坐标点。说人话,就是数轴中的点。我们不妨标出所有被变换的整数点,那么就会出现下图:

其中没有画红圈的点,是原空间中的点,画红圈的点是像空间中的点,就是一维生物画出的函数图像。
那我们看一个二维到二维的映射。
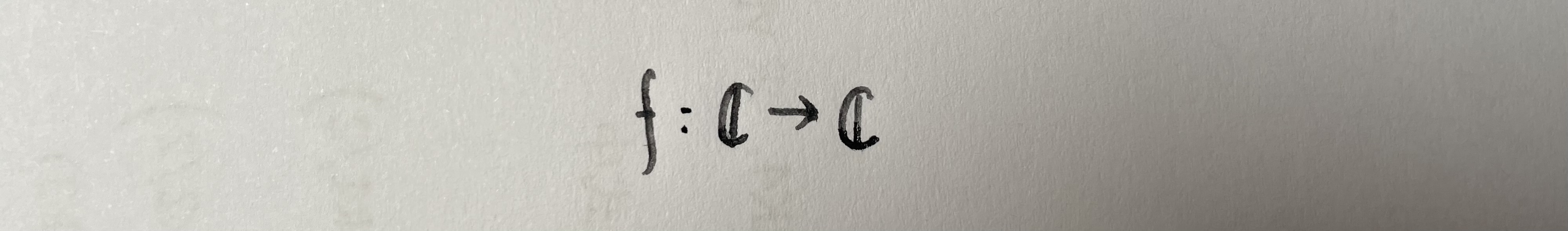
有同学这时候就要问了,诶自由基,你刚刚不是说C是复数集吗,怎么变成二维空间了?别急。众所周知,所有的复数都可以表示成z=a+bi。所以任意一个实数对(a,b)都可以表示一个复数。因此,实n维线性空间和复数集元素数相同。在集合论中,我们称两个元素数相同的集合等价,所以存在如下等价关系:
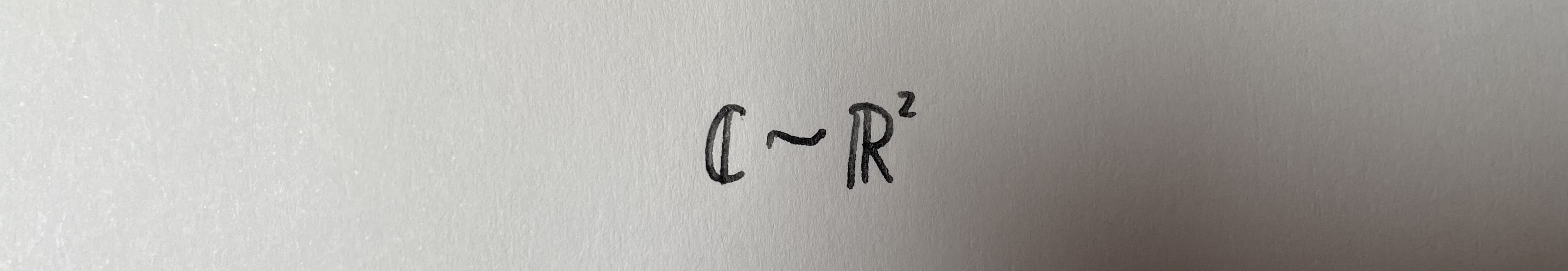
这个等价关系非常重要,他告诉我们复数集可以表示成一个平面,也就是复平面。因此,所有复函数都是二维空间到二维空间的映射,也就是投射二维空间的影子。
那这样的函数应该如何可视化?很明显我们不能直接飞升四维流形和复流形分析,因为我还没有那个本事,那些流形也看不见。所以我们还是要在二维空间中表示这些函数。这时候有学过向量场的同学肯定又要说了,用向量场不就行了吗?没错,向量场可以表示二维空间到二维空间的映射,但是这个方法在复分析中由于太过复杂,因此并不是很常用。
照葫芦画瓢,我们可以仿照一维生物的办法。所以让我们请出今天的第二个主角,黎曼zeta函数。
黎曼zeta函数由下面这个级数定义(放心,以后你还能遇见它):
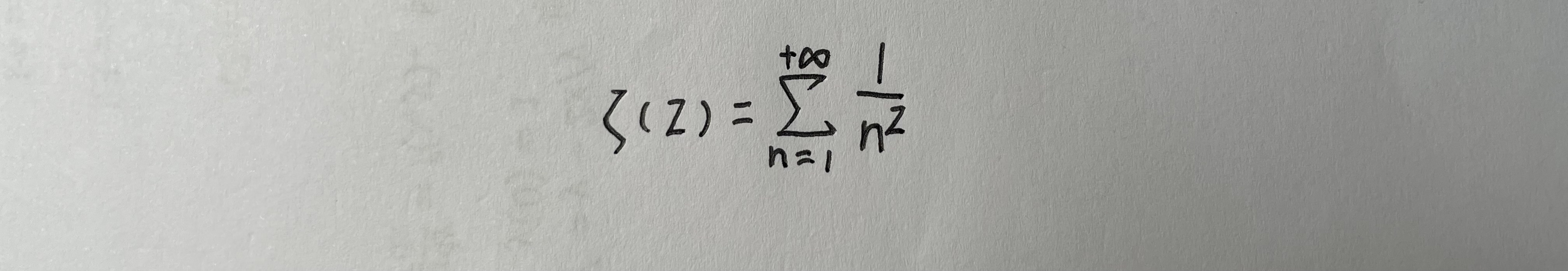
其中z是一个复数。今天我们暂且不讨论复数次方到底怎么计算,也不讨论黎曼函数到底是一个什么样的级数,我们只想画出它。这个活其实最初是黎曼做的。他先找到复平面上实轴和虚轴上的整数点,连成一个网格图,再变换这些坐标线,最后得到这样一幅图:
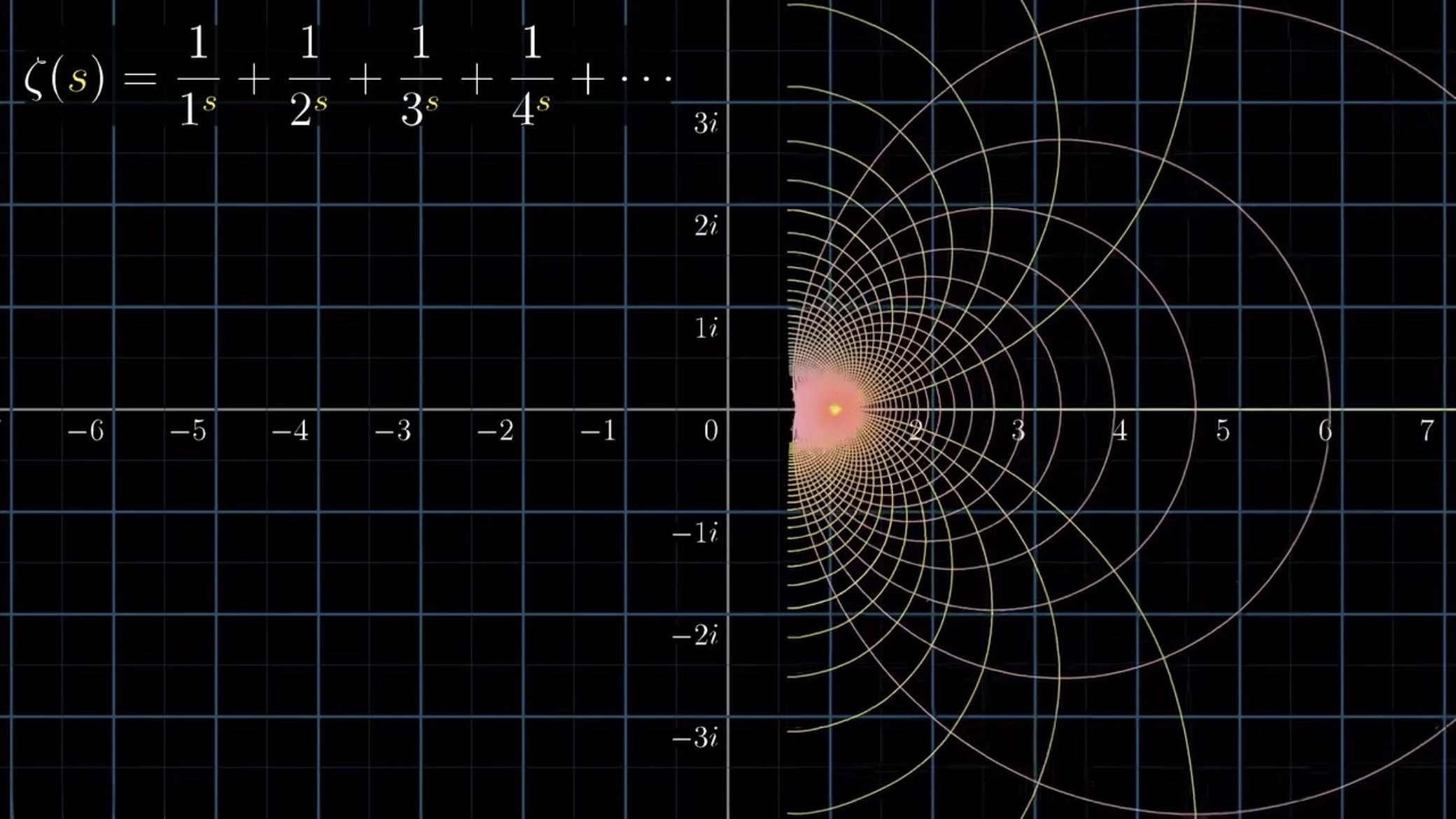
解析延拓之后是这样的:
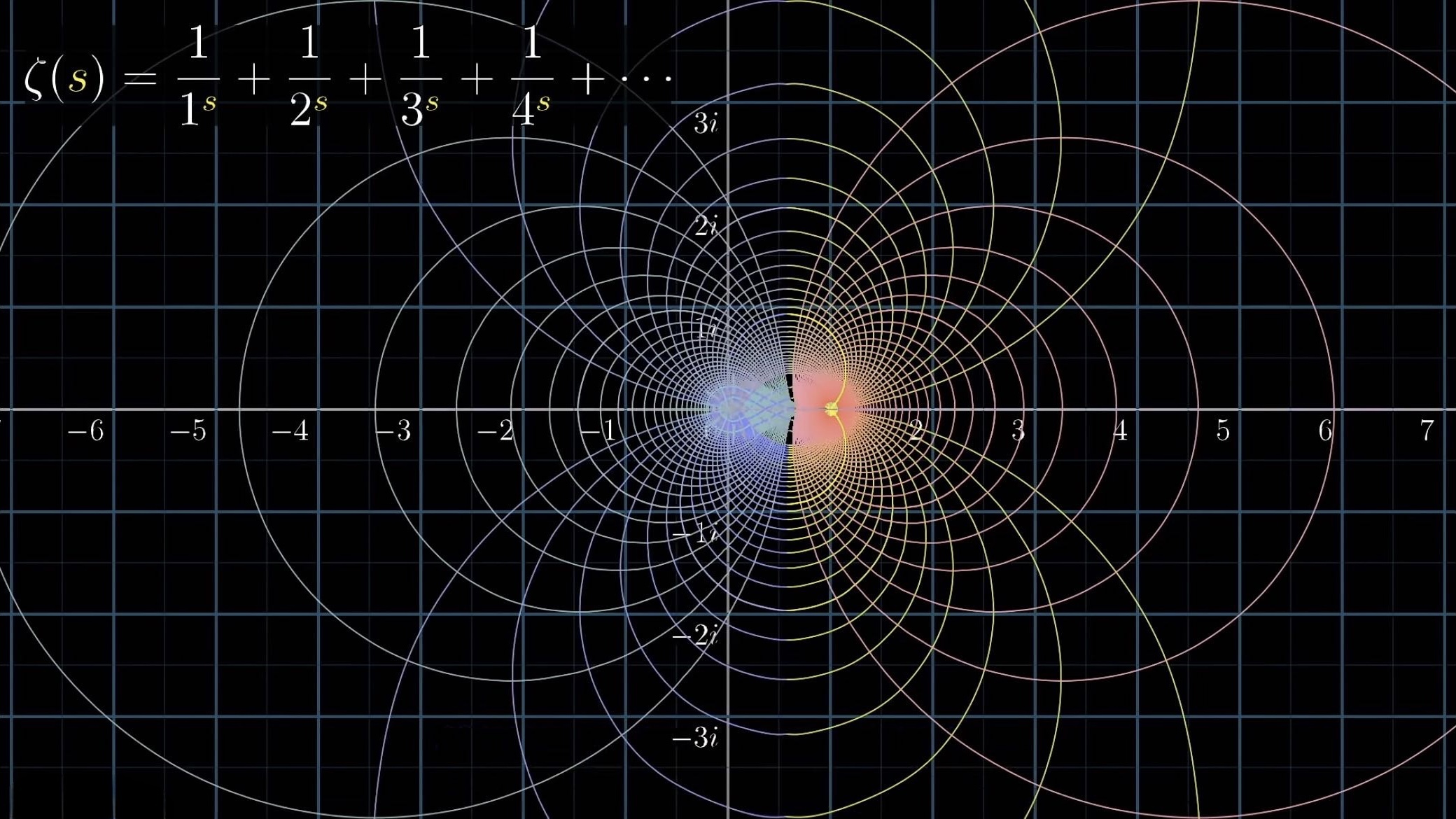
它真好看。
这就是映射的力量,投射空间的影子。那么,总有一天我们会看到世界的影子。
The end
参考文献:
[1]3Blue1Brown:【官方双语】黎曼zeta函数与解析延拓的可视化,bilibili,2017年2月20日
共3条回复
时间正序
