物理

[论坛资料室]速通复变函数 第二期

我这次是彻底换了个风格了，本期主题：

${\huge{无穷大的救赎}}$

${\large{救赎之一}}$

复平面，一个无限延展的地方，按理说是无边无际的旷野，但是有些数学家却想要给它加上一道边界

$那么这个边界在哪儿呢？数学家们给它取了个名字，叫做\infty ，也就是$无穷大，一个及其特殊的复数

这是多么美丽的名字，但又终究是虚幻的，必须要给它下一个明确的定义，它才能脱胎换骨，得到救赎

这时，有的数学家想起了一个禁令，一个万物之原点所被排斥的地方

$那个不能除以0的禁令$

$于是，真正的\infty出现了，它的定义式是$

$\infty=\frac{1}{0}$

${\tiny{是的你没看错，书上就是这么写的}}$

$\infty 最终救赎于禁令，它即是禁令，但它又打破了禁令，让除以0得以存在$

${\large{救赎之二}}$

数学家们决定把它融入这个数学世界的运算体系，又为它定义了它的四则运算法则

$(加法)~~~a+\infty =\infty +a=\infty ~~~(a\ne\infty )$

$(减法)~~~\infty -a=\infty ，a-\infty =\infty~~~(a\ne\infty )$

$(乘法)~~~a\cdot\infty =\infty\cdot a=\infty~~~(a\ne 0)$

$(除法)~~~\frac{a}{\infty}=0，\frac{\infty}{a}=\infty~~~(a\ne\infty)$

但是它还是会有缺陷，这是它永远无法填补的遗憾，它还是会导致一系列的无意义，就像

$\infty\pm\infty，0\cdot\infty，\infty\cdot 0，\frac{\infty}{\infty}，\frac{0}{0}$

这一系列式子

$伤心的事就让它过去了，数学家们还是会继续给它以救赎，他们定义\infty 的模长为+\infty ，但也就仅此而已$

那么问题又来了，它的实部、虚部和辐角呢？

数学家们却也只能说这些也都是无意义的

$就因为这些性质，导致对于其它任何复数z都有|z|＜+\infty ，这便又把\infty 孤立了，还顺便给了其它复数一个新头衔$有限复数

$\infty 本身就因禁令而生，最终也还是成了禁令，无法再存在了。。。吗？$

${\large{救赎之三}}$

$数学家们不甘心了，难道就因为复平面上没有\infty 的位置就放弃了吗？不，还可以设$

他们设想复平面上有一个理想点与之对应，此点称为无穷远点，加上无穷远点的复平面就称为扩充复平面

但是这个无穷远点到底在哪儿呢？

这个时候地理学家们坐不住了，他们说他们有一种方法，可以将一整个复平面压缩在一个球面上，这就是复球面，如图所示

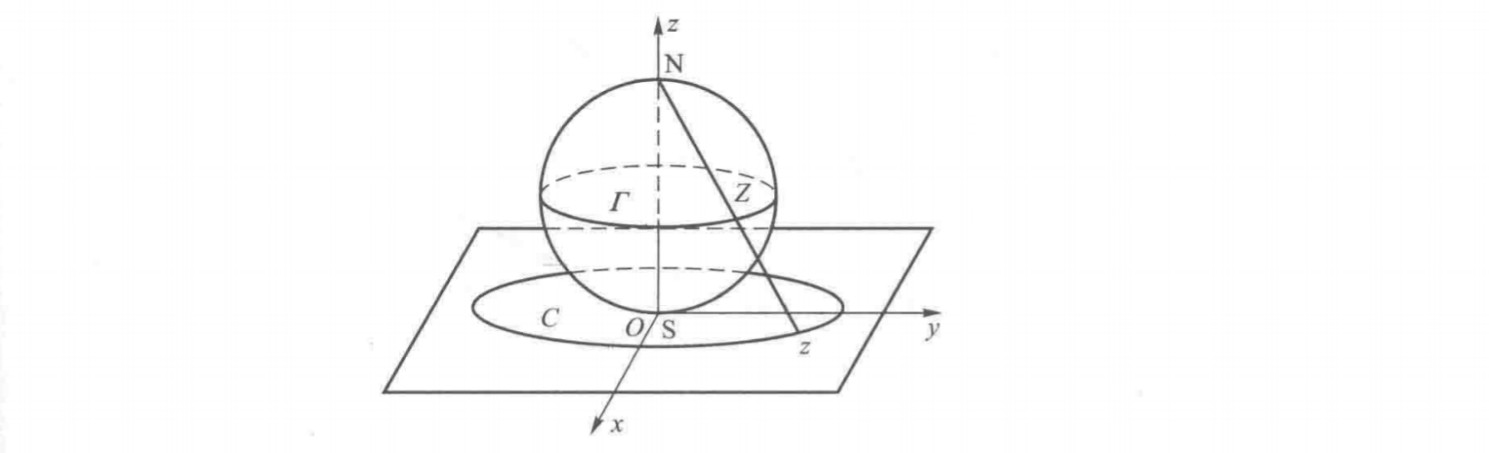
$这个球与复平面相切，切点为原点，即是这个球的南极S，然后过S作一条与复平面垂直的直线，即z轴，z轴与此球面交于N，即此球北极$

$我们称N为极点，再在此球面上取一点Z，作射线NZ，交复平面于z$

$这样，当Z不与N重合时，这一整个复平面上的所有有限点便能压缩到这个球面上，z是Z在复平面上的投影，Z是z在复球面上的映射$

$那么N是什么呢？$

$对于每一个以原点为圆心的圆周C，都会在复球面上有一个映射\Gamma ，即此球一纬线$

$显然地，当圆周C的半径越来越大的时候，纬线\Gamma 就会越来越接近极点N$

$所以当C的半径等于+\infty 的时候，\Gamma 就会与N重合，即N就是无穷远点在复球面上的映射$

这样，扩充复平面上的每一个点都在复球面上有了归宿，理想点无穷远点就是复球面的极点

$那么，我们也能知道，复平面上的\infty 是没有符号的，或者说，它和0一样，也拥有任何符号$

无穷原点现在就有了具体的化身，在扩充复平面上放眼望去，最终都会是无穷远点，最远的边缘，最终都收敛于同一点

它让每一条直线都能够相交，即使是无法相交的平行线

$所以，我们就可以定义一下无穷远点的邻域了，即是|z|＞M，其中实数M＞0$

$也就是说，无穷远点的邻域就是包括无穷远点自身在内的圆周|z|=M的外部$

$而不包括无穷远点自身，只满足|z|＞M的点集就是无穷远点的去心邻域，即M＜|z|＜+\infty $

$\infty 既是禁令的产物，又是理想的化身，它最终还是救赎于理想$

嚎！第二期就到这儿，希望这种风格大家能喜欢，感谢大家！敬请期待第三期！