物理

[论坛资料室]柯西，欧拉，与积分的艺术

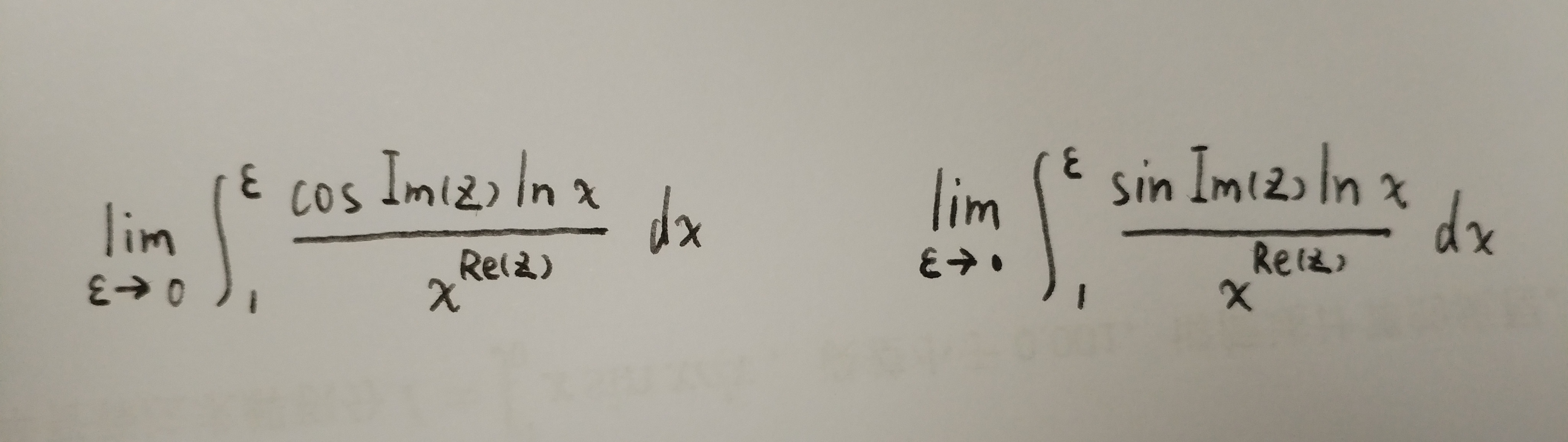
       这是什么玩意？你很懵。很明显，这两个被积函数在零处都不收敛。这怎么办？你不能轻言放弃。于是你想到了用数值方法计算。虽然精度不是很高，但是死马当活马医，也只能这样了。

       你打开电脑，输入程序，使用了辛普森方法，复化梯形公式，试图计算积分的值。但是你发现，这个积分在零点附近剧烈震荡，连计算机都无法处理。

       这下没办法了，你关掉电脑，随手从书架上拿出来一本《复变函数》。等等，复变函数？对啊，为什么不尝试复变呢？于是你拿出草稿纸，写下一个公式：

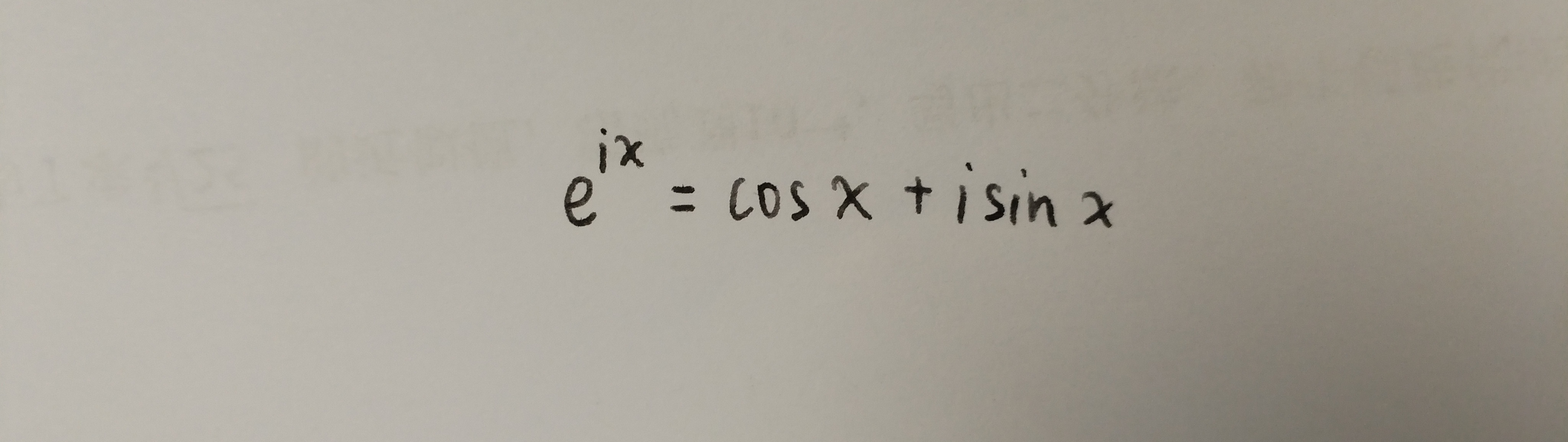
       这是著名的欧拉公式。于是，不难发现，第一个被积函数的分子可以写成如下形式：

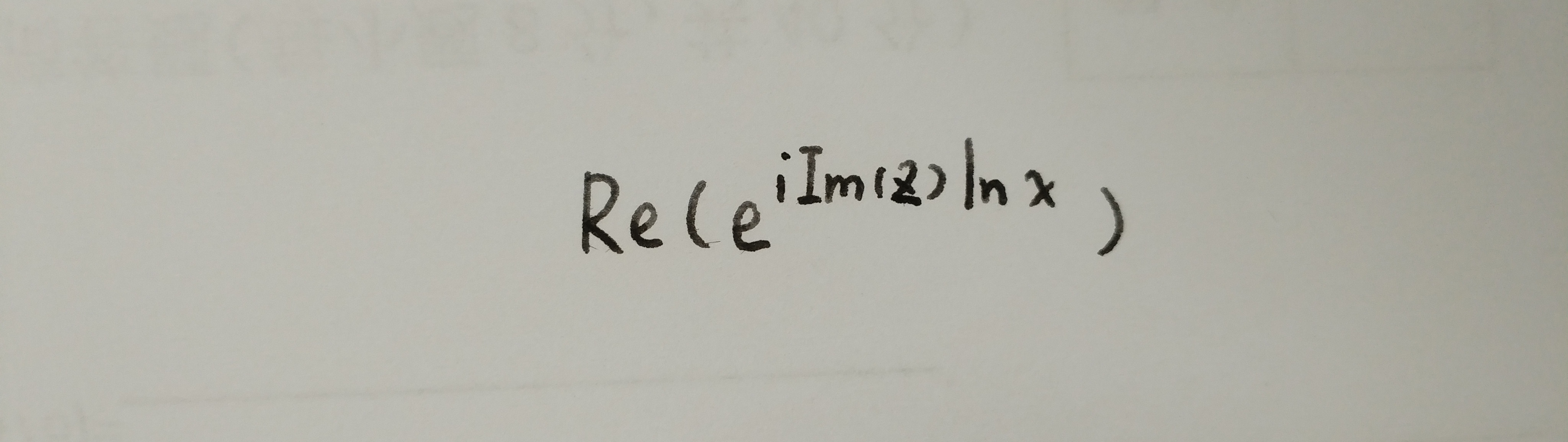
        把ln x挪到下面去：

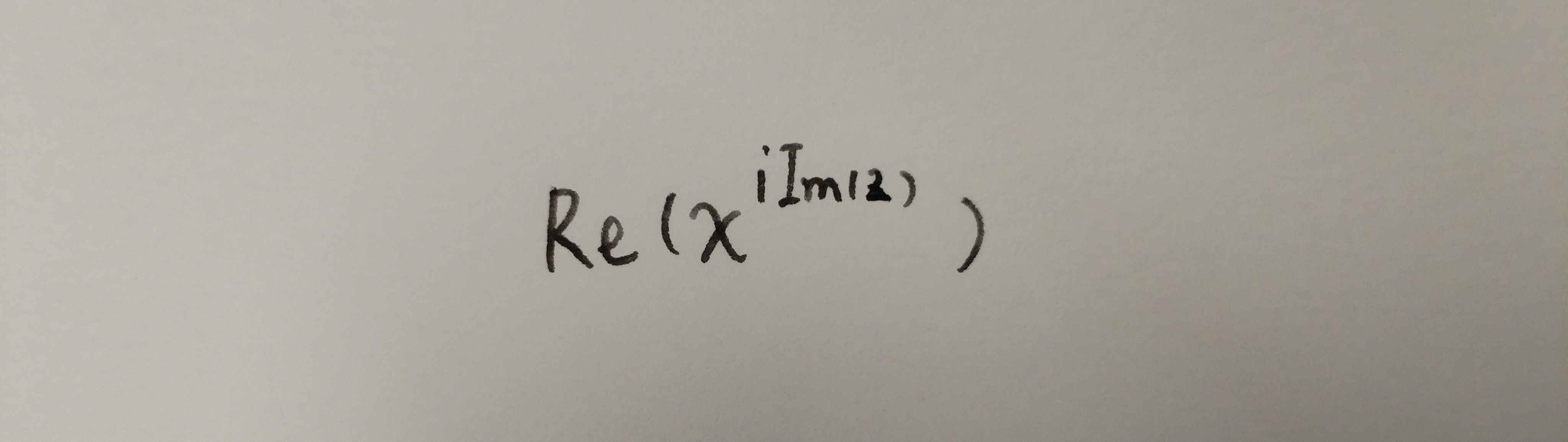
      又因为x的Re(z)次方一定是实数，所以整个被积函数可以写成如下形式：

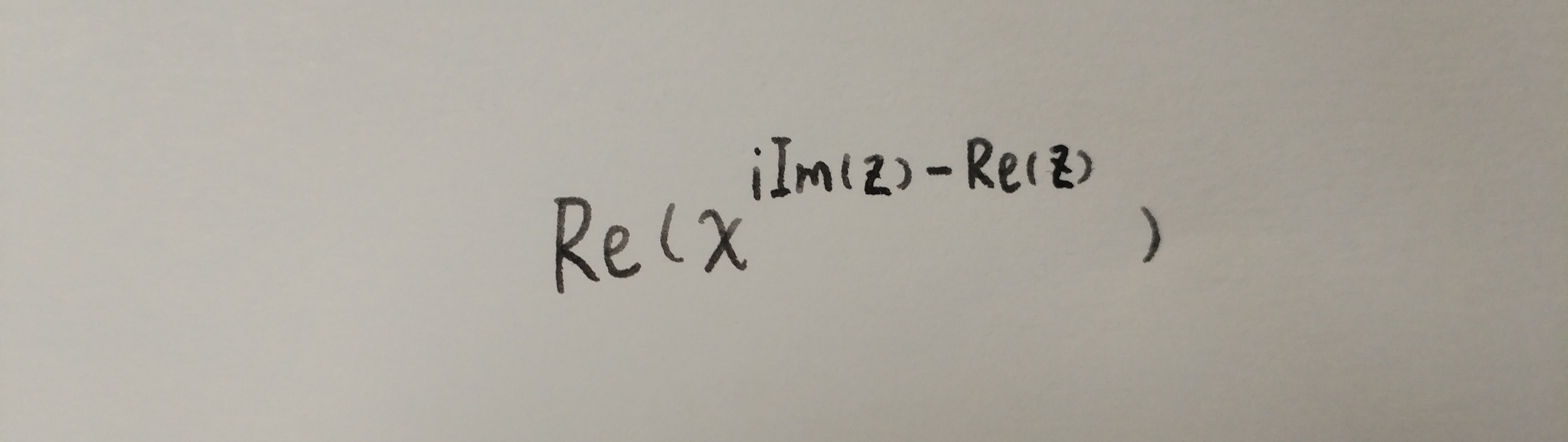
      而实部提取符号是可以提到积分前的，所以就得到如下等式：

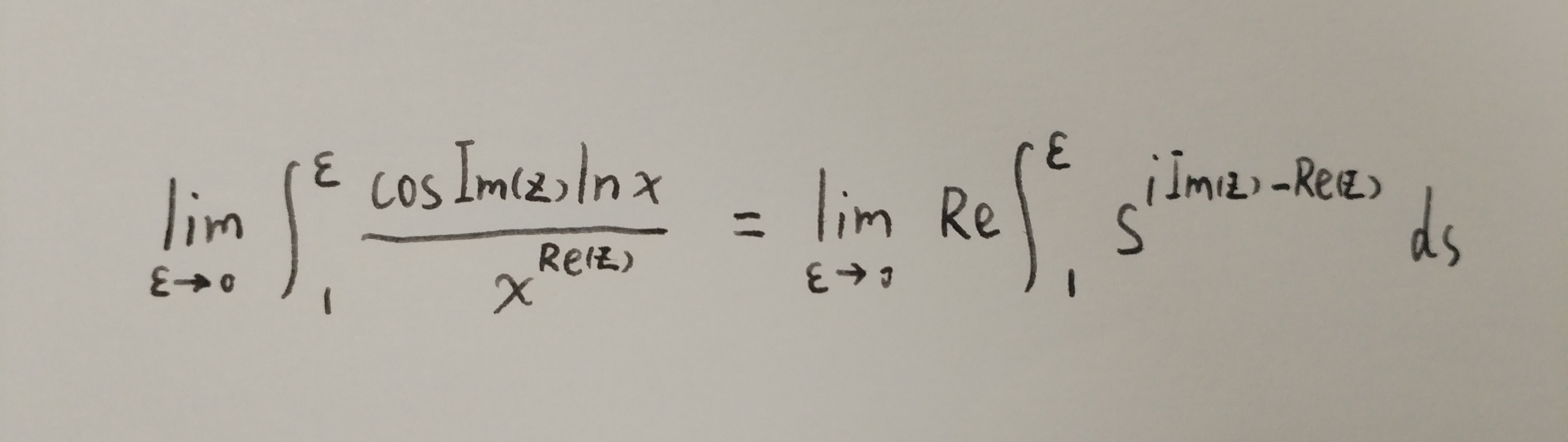
      同理得到：

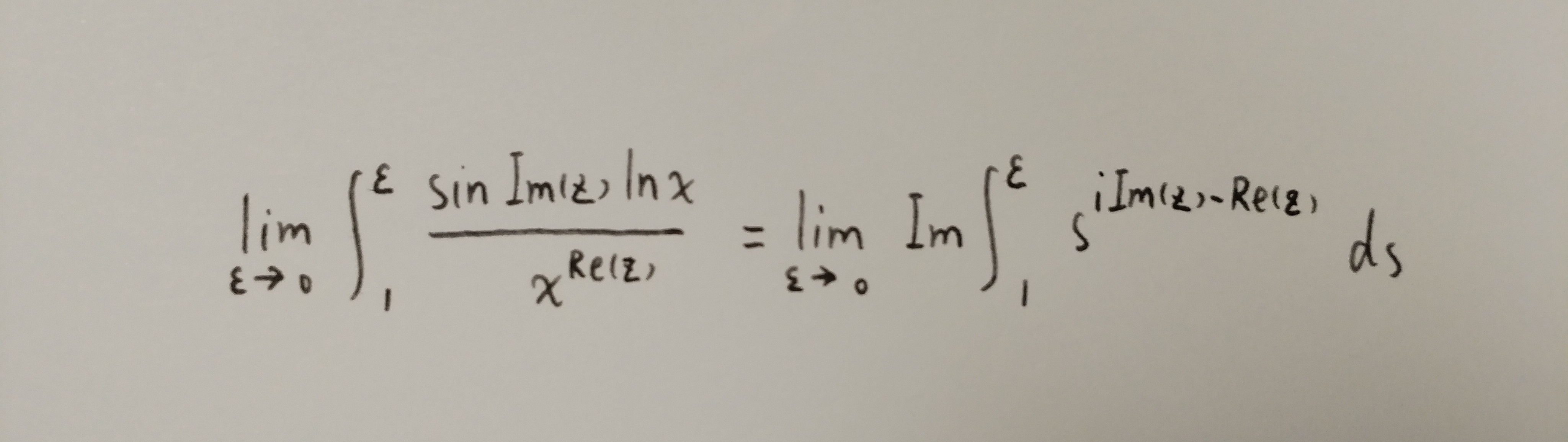
        这样，被积实变函数就成了复变函数。对于复变函数的积分，我们自然会想到柯西定理。既然这两个函数在实轴上剧烈震荡，那我们选择一条绕过实轴的路径γ，想怎么取怎么取，只需要这条路径从零出发，到一结束就可以了。当然，因为我们使用的是数值方法，所以这条路径只需要起点接近于0。比如我们可以选择$$10^{-16}\mathrm{i}$$来作为起点。所以我们最后只需要计算下面的积分：

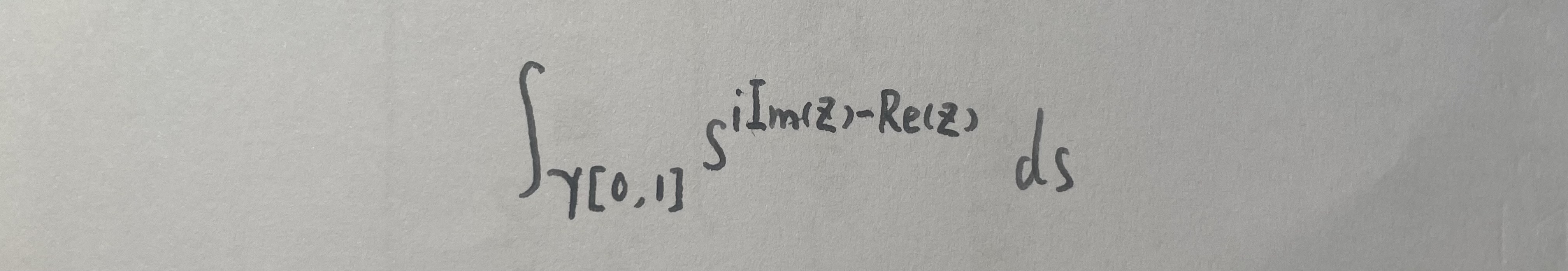
      其中Re(z)和Im(z)是常数。

      这样我们的工作就简化很多。积分我就不算了，毕竟讲怎么路径积分又得写大一篇文章。

       看来柯西和欧拉联手帮我们解决了一大积分问题。所以这也印证了我们文章的标题：柯西，欧拉，与积分的艺术。

        The End

（好水啊好水啊，算了，下次发个长一点的吧）

参考文献：

[1]泰勒猫爱丽丝：100美元的数学题：震荡的积分与绕远路的捷径，bilibili，7月18日

[2]活性自由基：黎曼zeta函数零点方程的推导与简化，未发表