共9条回复
时间正序
攒拳怒目的坚果
9月前
唉，数学区还是太冷清了，公布一下卷怪关于第一问的解答：（以后公布第二问）
$(1)记f_y(x)=\begin{cases}1,x\lt y\\0,x≥y\end{cases},则知f_y(x)可积,则$
$min\{x_i,x_j\}=\int_{0}^{+∞}f_{x_i}(x)f_{x_j}(x)dx,min\{y_i,y_j\}=\int_{0}^{+∞}f_{y_i}(x)f_{y_j}(x)dx,min\{x_i,y_j\}=\int_{0}^{+∞}f_{x_i}(x)f_{y_j}(x)dx$
$故\sum_{i=1}^n min\{x_i,x_j\}=\sum_{i=1}^n \int_{0}^{+∞}f_{x_i}(x)f_{x_j}(x)dx$
$=\int_{0}^{+∞}\sum_{i=1}^n f_{x_i}(x)f_{x_j}(x)dx=\int_{0}^{+∞}(\sum_{i=1}^n f_{x_i}(x))^2dx$
$同理，有\sum_{i=1}^n min\{y_i,y_j\}=\int_{0}^{+∞}(\sum_{i=1}^n f_{y_i}(x))^2dx,$
$\sum_{i=1}^n min\{y_i,y_j\}=\int_{0}^{+∞}(\sum_{i=1}^n f_{x_i}(x))(\sum_{i=1}^n f_{y_j}(x))dx$
$故原题⇔\int_{0}^{+∞}(\sum_{i=1}^n f_{x_i}(x))^2dx+\int_{0}^{+∞}(\sum_{i=1}^n f_{y_i}(x))^2dx≥2\int_{0}^{+∞}(\sum_{i=1}^n f_{x_i}(x))(\sum_{i=1}^n f_{y_j}(x))dx$
$⇔\int_{0}^{+∞}(\sum_{i=1}^n f_{x_i}(x))^2+(\sum_{i=1}^n f_{y_i}(x))^2-2(\sum_{i=1}^n f_{x_i}(x))(\sum_{i=1}^n f_{y_j}(x))dx≥0$
由均值知显然成立
1条评论
- 1
攒拳怒目的坚果
9月前
第二问:
$先证欧拉定理:n=\sum_{d|n}φ(d)$
$证:\sum_{d|n}φ(d)=\sum_{d|n}φ(\frac{n}{d})=\sum_{d|n}\sum_{(x,\frac{n}{d})=1,x≤\frac{n}{d}} 1$
$=\sum_{d|n}\sum_{(xd,n)=1,x≤\frac{n}{d}} 1=\sum_{d|n}\sum_{(t,n)=d,t≤n} 1=\sum_{t≤n}\sum{d|n,d=(t,n)} 1$
$=\sum_{t≤n} 1=n,故成立$
$回到原题,记g_n(d)=\begin{cases} 1,d|n\\0,d\nmid n\end{cases}$
$则(x,y)=\sum_{d|(x,y)}φ(d)=\sum_{d|x,d|y}φ(d)=\sum_{d=1}^{+∞}φ(x)g_x(d)g_y(d)$
这已经整理成了与第一问一样的形式，故与第一问同理可证
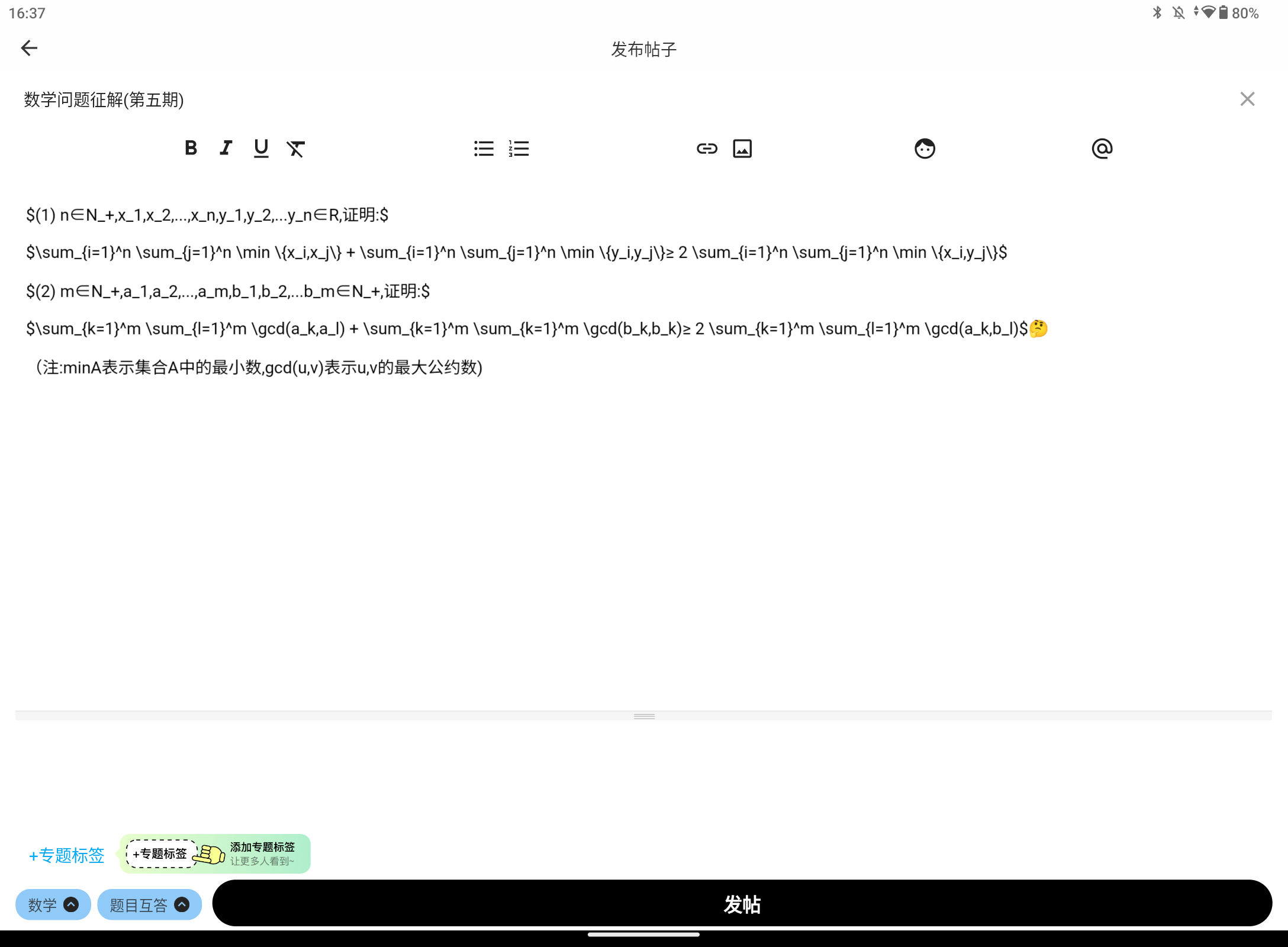
第一题似乎可以强化一下