共5条回复
时间正序
LEAP-1C-Fourier
9月前
2024/08/07
难度：一试
来源：23年高联一试第8题
题干：
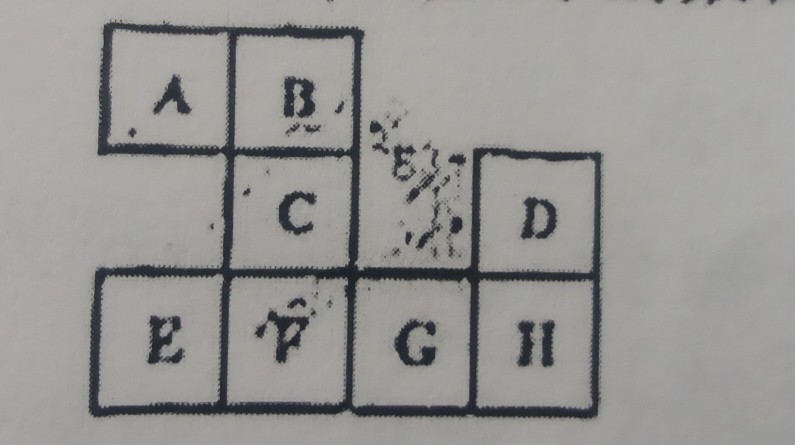
8张标有$A,B,C,D,E,F,G,H$的卡片按如下方式排列，现逐一取走这些卡片，要求每次取走一张卡片时，该卡片与剩下的卡片中至多一张有公共边，则取走这八张卡片的不同次序的数目为？
8条评论
- 1
mo：是啊是啊，最近都没活跃了
9月前
好吧，是我错了，但是确实，是dp
转移公式，f(m，n)=2^(n+m)+f(m-1,n)+f(m,n-1)
特殊情况：f(0,n)=2^(n+1)
特殊情况：f(m,0)=2^(m+1)
稍微题一嘴，这是我学信竞学的，数学还没学到这
LEAP-1C-Fourier
9月前
0807标答
取卡片规则可以解释为：
（i）若顶点$P$已取走，则一下每步取当前标号最小或最大的顶点，直至取完
（ii）若顶点$P$未取走，则必为某个$G(m,n)$（$m,n$$\ge$$0$）的情形，此时若$m$$=$$0$,则将$P$视为$-1$号顶点，归结为（i）的情形；若$m$$\neq$$0$，$n$$=$$0$，则将$P$视为1号顶点，归结为（i）的情形；若$m,n$$\ge$$1$，则当前可取$P$或$-m$号顶点或$n$号顶点，分别归结为（i）或$G(m-1,n)$或$G(m,n-1)$的情形
设$G(m,n)$的符合要求的顶点选取次序数为$f(m,n)$，本题所求即为$f(2,3)$.
由（i）（ii）知$f(m,0)$$=$$2^m+1$($n$$\ge$$0$)，且
$f(m,n)$$=$$2^m+n$$+$$f(m-1,n)$$+$$f(m,n-1)$($m,n$$\ge$$1$)
由此可依次计算得
$f(1,1)$$=$$12$，$f(1,2)$$=$$f(2,1)$$=$$28$，$f(1,3)$$=$$60$，$f(2,2)$$=$$72$，$f(2,3)$$=$$164$，即所求数目为164
3条评论
mo：是啊是啊，最近都没活跃了
9月前
你题目中的图和你题解不同，求的是f(3,3)
LEAP-1C-Fourier
9月前
\ge为$\ge$，\neq为$\neq$
LaTeX 打的有的小问题，谅解一下
LEAP-1C-Fourier 回复 mo：是啊是啊，最近都没活跃了
9月前
丸啦！
我待会去看看标准解蛤