物理 初中数学考点(中考生必看)
第一章 实数 第八章 一次函数
第二章 整式 第九章 二次函数
第三章 分式 第十章 反比例函数
第四章 方程(组)与不等式(组) 第十一章 旋转
第五章 几何部分 第十二章 圆
第六章 三角形 第十三章 三角函数
第七章 四边形 第十四章 统计与概率
↓自然数—[0与正整数 ↓正整数
第一章: ↓整数—[负整数 ↓正有理数—[正分数
实数分类1:实数—[ 有理数 [ 有理数的分类1:有理数—[0
↑ ↑分数—[正分数 ↑负有理数—[负整数
↑ ↑负分数 ↑负分数
↑无理数 [ 正无理数
↑负无理数
———————————————————————————————————————————————————————————————————————————————————
↓正整数 ↓正整数
↓正有理数—[ 正分数 ↓0
↓正实数—[ 正无理数 整数—[负整数
实数分类2:实数—[0 ↓负整数 有理数分类2:有理数—[分数—[负分数
↑负实数—[负有理数—[负分数 ↑正分数
↑负无理数
—————————————————————————————————————————————————————————————------------------
算数平方根:如果一个正数x的平方等于a,即(x^2=a),那么正数x叫做a的算术平方根。
记作√a(a大于等于0)
0的算术平方根为0
平方根:如果一个数x的平方根等于a,即(x^2=a),那么数x叫做a的平方根。
平方根的性质:正数有两个平方根(一正一负)它们互为相反数。
0只有一个平方根,就是它本身。
负数没有平方根
立方根:x^3=a→x=³√a
立方根的性质:正数的立方根是正数
0的立方根是0
负数的立方根是负数
数轴:数轴是规定了原点、正方向、单位长度的一条直线
相反数:(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0
(2)相反数的和为0,即a+b=0(a、b互为相反数)
绝对值:|a|=a(a>0)或=0(a=0)或=-a(a<0)
绝对值的几何意义:数轴上表示某数的点与原点之间的距离。
倒数:乘积为1的两个数互为倒数,0没有倒数
若a≠0,那么a的倒数是a/1
有理数乘法的运算定律:
1.交换律:AB=BA
2.结合律=(AB)C=A(BC)
3.分配律=A(B+C)=AB+AC
比较两个数的大小:(1)负数<0<正数,任何一个正数都大于一切负数
(2)数轴上的点表示的有理数,左边的数总比右边的数小
(3)两个正数比较大小,绝对值大的数就大;两个负数比较大小,绝对值大的数反而小
(4)两数相乘(或相除),同号得正>0,异号的负<0
有理数乘方的法则:(1)正数的任何次幂都是正数
(2)负数的奇次幂是负数;负数的偶次幂是正数
当n为正奇数时:(-a)^n=-a^n或(a-b)^n=-(b-a)^n
当n为正偶数时:(-a)^n=a^n或(a-b)^n=-(b-a)^n
科学计数法:把一个大于10的数记成10^n*a 的形式,其中a是整数数位只有一位的数,这种记数法叫做科学计数法。
非负数的性质:若|a|+b^2+√c=0,则a=0,b=0,c=0
二次根式:形如√a(a大于等于0)的代数式叫做二次根式。
当a>0时,√a表示a的算术平方根
其中√0=0
二次根式的性质:双重非负性
口诀:平方之后再开方,出来之后带框框。
二次根式的乘法:√a×√b=√a b(a大于等于0,b大于等于0)反之亦成立
二次根式的除法:√a÷√b=√a÷b(a大于等于0,b≠0)
最简二次根式:(1)被开方数不含字母
(2)被开方数不含开得尽方的因数或因式
同类二次根式:几个二次根式化简成最简二次根式后,如果被开方数相同,那么这几个二次根式是同类二次根式。
————————————————————————————————————————————————————————————————————————————————————
第二章:
单项式:由数和字母的乘积组成的式子,单独的一个数或一个字母也是单项式,如:z,-2.
单项式中的数字因数叫做系数
单项式中的所有字母的指数和叫做次数
多项式:几个单项式的和叫做多项式
组成多项式的每个单项式叫项
组成多项式的单项式的个数叫项数
多项式中次数最高项的次数为该多项式的次数
整式的加减:本质上就是合并同类项,如果有括号要先去掉括号,再合并同类项。
合并同类项的法则:将同类项的系数相加,字母及其指数不变
整式的乘法:(1)单项式乘法法则:单项式相乘,把它们的系数、相同字母分别相乘,单独含有字母连同指数不变。
(2)单项式与多项式相乘:用单项式去乘多项式的每一项,再把所得的积相加。
(3)多项式与多项式相乘:多项式与多项式相乘,先用一个多项式中的每一项乘另一个多项式的每一项,再把所得的积相加。
整式的除法:(1)单项式除以单项式:把系数、同底数幂分别相除,对于只在被除式里含有的字母,则连同它的指数不变。
(2)多项式除以单项式:多项式除以单项式,先把这个多项式的每一项除以单项式,再把所得的商相加。
幂的运算的相关公式:a^m×a^n=a^m+n
a^m÷a^n=a^m-n
(a^m)^n=a^mn
(ab)^n=a^n×b^n
平方差公式:(a+b)(a-b)=a^2-b^2
完全平方公式:(a±b)^2=a^2±2ab+b^2
分解因式:把一个多项式化成几个式子的积的形式
一般方法:(1)提公因式法
(2)公式法
(3)十字相乘法
步骤:(1)先看各项是否有公因式,若有,则先提取公因式
(2)再看能否使用公式法
(3)十字相乘法可对二次三项式试一试
(4)因式分解最后结果必须是几个整式的乘积,否则不是因式分解
(5)因式分解的结果必须进行到每个因式在有理数范围内不能再分解为止
第三章
分式的定义:形如A/B,A、B是整式,且B中含有字母叫做分式(B≠0)
分式的基本性质:分式的分子和分母同时乘以(或除以)同一个不为0的整式,分式的值不变
最简分式:一个分式和分子没有公因式时,这个分式成为最简分式
约分时,一般将一个分式化成最简分式或整式
分式的四则运算:
(1)a/c±b/c=a±b/c
(2)a/b±c/d=ad±bc/bd
(3)a/b×c/d=ac/bd
(4)a/b÷c/d=a/b×d/c
分式方程定义:分母中含有未知数的方程叫做分式方程
分式方程的解法:一化二解三检验
1.化简去分母(方程两边同时乘以最简公分母,将分式方程化简
2.按解整式方程步骤求出未知数的值
3.验根(求出未知数的值后必须验根, 因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根)
使最简公分母为零的整式方程的根不是原方程的根(是增根)
使最简公分母不为零的整式方程的根是原方程的根
第四章
等式的性质:等式两边加(或减)同一个数(或式子),结果任然相等
等式两边同时乘一个数或式,或除以同一个不为零的数或式,结果任然相等
一元一次方程:一般式:ax+b=0(x是未知数,a、b是常数,且a≠0)
解方程步骤:整理方程→去分母→去括号→移项→合并同类项 系数化为1→得到方程的解
解二元一次方程组的基本思想:消元思想
基本方法:代入消元法和加减消元法
解三元一次方程的基本方法是:三元(消元)→二元(消元)→一元
一元二次方程:方程两边都是整式,只含有一个未知数(一元),并且未知数的最高次数项是2(二次)的方程,叫做一元二次方程
一般形式:ax²+bx+c=0(x为未知数,a、b、c是常数,且a≠0)
解一元二次方程的方法:开平方法,配方法,公式法。
注意:(如:x=-b±√b²-4ac/2a)这种叫做一元二次方程的求根公式
根的判别式为:δ=b²-4ac
① δ>0←=→方程有两个不等式的实数根:x小1,小2=-b±√b²-4ac/2a
② δ=0←=→方程有两个相等的实数根:x小1=x小2=-(b/a)
③ δ<0←=→方程没有实数根
韦达定理:如果一元二次方程 ax²+bx+c=0(a≠0)的两根为x小1,x小2
那么,就有 x小1+x小2=-(b/a),x小1×x小2=c/a
(注意:运用根于系数的关系的前提是b²-4ac大于等于0)
常用公式:(1)行程问题: 距离=速度×时间 速度=距离/时间 时间=距离/速度
(2)工程问题: 工作量=工效×工时 工效=工作量/工时 工时=工作量/工效
(3)比率问题: 部分=全体×比率 比率=部分/全体 全体=部分/比率
(4)顺逆流问题: 顺流速度=静水速度+水流速度 逆水速度=静水速度-水流速度
(5)商品价格问题: 售价=定价×折×1/10 利润=售价-成本 利润率=售价-成本/成本×100%
(6)周长,面积,体积: C圆=2πR S圆=πR² C长方形=2(a+b) S长方形=ab C正方体=4a S正方体=a² S环形=π(R²-r²)
V长方体=abc V正方体=a² V圆柱=πR²h V圆锥=1/3πR²h
不等式的性质:不等式的两边都加上(或减去)同一个数(或式),不等号方向不变。
不等式的两边都乘以或除以一个正数,不等号方向不变。
不等式的两边都乘以或除以一个负数,不等号方向改变。
解不等式口诀:同大取大,同小取小,大小小大中间找,大大小小找不到
第五章
直线公理:两点确定一条直线
线段公理:两点之间,线段最短
两点之间的距离:连接两点的线段的长度叫做两点之间的距离
角的换算:1度=60撇 1撇=60撇撇
1周角=360度 1平角=180度
互余,互补:两个角的和等于直角,这两个角互余
两个角的和等于平角,这两个角互补
同角或等角的余角相等
同角或等角的补角相等
垂线的性质:1.过一点有且只有一条直线与已知直线垂直
2.连接直线外一点与直线上各点的所有线段中,垂线最短
平行公理:经过直线外一点有切只有一条直线与已知直线平行
平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行
平行线的性质:1 两直线平行,同位角相等
2 两直线平行,内错角相等
3 两直线平行,同旁内角互补
平行线的判断:1 同位角相等,两直线平行
2 内错角相等,两直线平行
3 同旁内角互补,两直线平行
平移的性质:平移前后的图形相等
对称轴:如果一个图形沿某条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴
轴对称的性质:(1)轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线
(2)角平分线上的点到角两边距离相等
(3)线段垂直平分线上的任意一点到线段两个端点的距离相等
(4)与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
(5)轴对称图形上对应线段相等、对应角相等
最短路径问题:
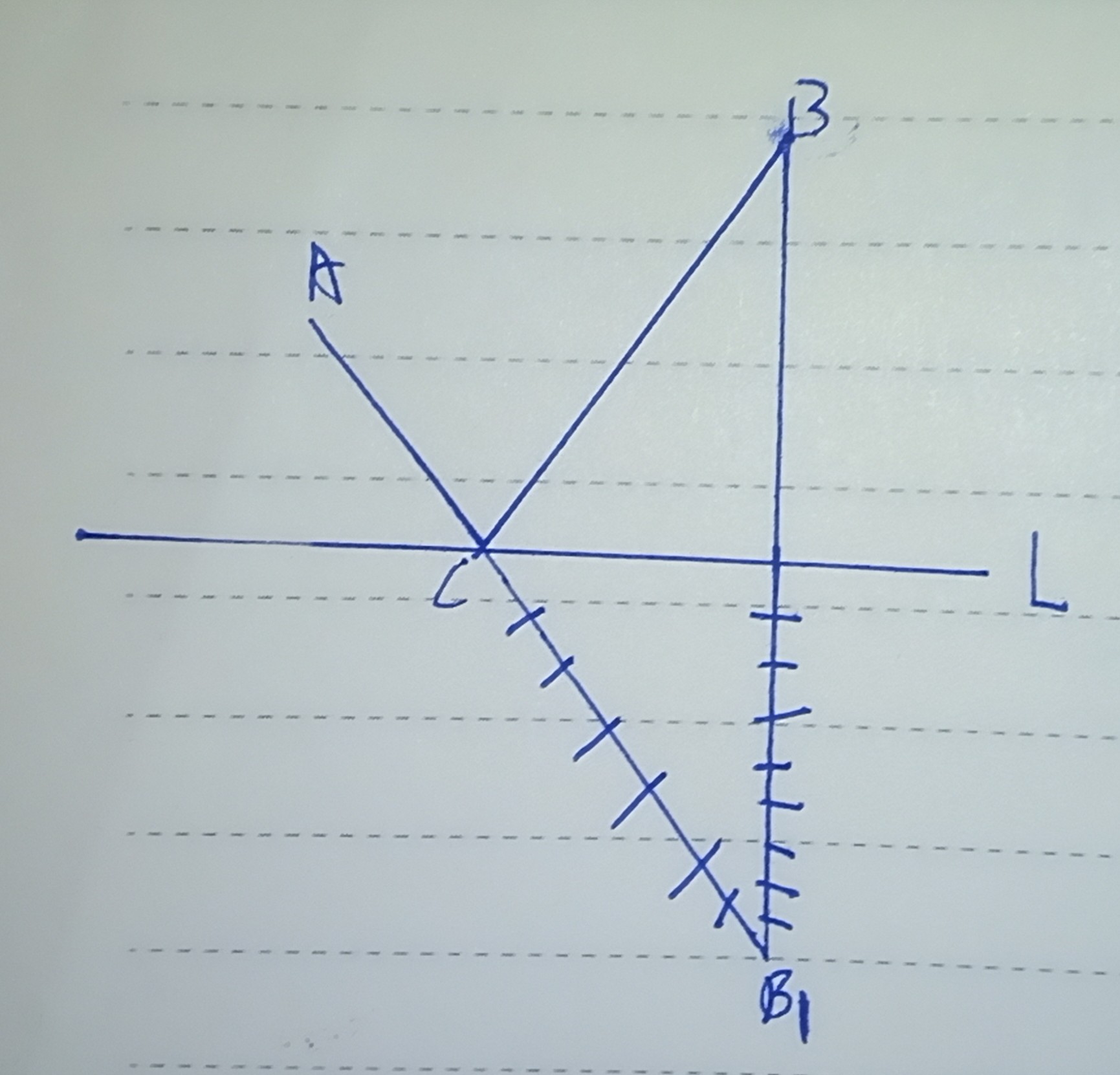
如图,已知点A、B在直线L的同侧
现在L上求一点C,使CA+CB最小,作法如下:↓
作点B(或点A)关于L的对称点B1,连接AB1,交L于C,那么C就可以使AC+BC最短
勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a²+b²=c²
勾股定理逆定理:如果三角形三边a b c满足a²+b²=c²
那么这个三角形是直角三角形
相似的判定方法:1 平行于三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似;(预备定理)
2 如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似;(角角对应)
3 如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似;(边比角边比)
4 如果两个三角形的三组对应边的比相等,那么这两个三角形相似;(边边边比)
相似三角形的性质:①相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比
②相似三角形周长的比等于相似比
③相似三角形面积的比等于相似比的平方
如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比。
位似图形上任意一对对应点到位似中心的距离之比等于位似比。
第六章:
三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边。
正多边形:在平面内,各个角都相等,各条边都相等的多边形叫做正多边形。
公式与性质:(1)三角形的内角和:180度
(2)三角形外角的性质:1:三角形的一个外角等于和它不相邻的两个内角的和
2:三角形的一个外角大于任何一个和它不相邻的内角
(3)多边形内角和公式:n边形的内角和等于(n-2)×180度
(4)多边形对角线的条数:①从n边形的一个顶点出发可以引(n-3)条对角线,把多边形分成(n-2)个三角形。
②n边形共有n(n-3)/2条对角线
全等三角形的性质:全等三角形的对应点相等,对应边相等。
三角形全等的判断公理及推论:(1)边角边简称SAS
(2)角边角简称ASA
(3)边边边简称SSS
(4)角角边简称AAS
(5)斜边和直角边相等的两直角三角形(HL)
角平分线:(1)角平分线的性质:在角平分线上的点到角的两边的距离相等
(2)角平分线推论:角的内部到角的两边的距离相等的点在角的平分线上
等腰三角形:等腰三角形的两个底角相等(等边对等角)
等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合,简称为三线合一
等边三角形:特点:三边相等,三个内角相等,等于60度
判定:三个内角相等的三角形是等边三角形
三条边相等的三角形叫等边三角形
有两个底角是60度的三角形叫等边三角形
直角三角形:直角三角形中,30度角所对的直角边等于斜边的一半
直角三角形斜边上中线等于斜边的一半
三角形的中位线的性质:三角形的中位线平行于三角形的第三边,且等于第三边的一半
第七章
平行四边形定义:有两组对边分别平行的四边形叫做平行四边形
平行四边形的性质:平行四边形的对边相等,对角相等,对角线互相平分
平行四边形是中心对称图形,对角线的交点是对称中心
平行四边形的判定:1.两组对边分别相等的四边形是平行四边形
/ 2.两组对角分别相等的四边形是平行四边形
/ 3.对角线互相平分的四边形是平行四边形
/ 4.一组对边平行且相等的四边形是平行四边形
注:平行四边形的定义也是一种判定
矩形的定义:有一个角是直角的平行四边形叫做矩形
矩形的性质:矩形的四个角都是直角,对角线互相平分且相等
矩形是轴对有两称的图形,即经过对边中点的两条直线是对称轴(也是中心对称图形)
矩形判定定理:①有一个角是直角的平行四边形叫做矩形
②对角线相等的平行四边形是矩形
③有三个角是直角的四边形是矩形
菱形的定义:邻边相等的平行四边形叫做菱形
菱形的性质:菱形的四条边都相等,两条对角线互相垂直,并且每一条对角线平分一组对角
菱形是轴对称图形,两条对角线所在的直线是对称轴(也是中心对称图形)
菱形的判定定理:①组邻边相等的平行四边形是菱形
②对角线互相垂直的平行四边形是菱形
③四边形相等的四边形是菱形
S菱=1/2ab(a、b为两条对角线)=底×高
正方形的定义:一个角是直角的菱形或邻边相等的矩形
正方形的性质:四条边都相等,四个角都是直角
正方形既是矩形,有是菱形
正方形的判定:(1)邻边相等的矩形是正方形
(2)有一个角是直角的菱形是正方形
第八章:
一次函数:y=kx+b(k≠0)
特别地,当b=0时,称y是x的正比例函数
k>0=[ b>0
↑b=0
↑b<0
k<0[ b>0
↑b=0
↑b<0
已知两点坐标求函数解析式:常用方法:待定系数法
解析步骤:(1)设解析式
(2)由题意列出方程(或方程组 )
(3)解方程(或方程组)
(4)写出函数解析式
当k1=k2时,直线y=k1x+b1和直线y=k2x+b2平行
两条直线y=k1x+b1和直线y=k2x+b2的交点坐标就是方程组[ y=k1x+b1 的解
↑y=k2x+b2
第九章
二次函数的解析式三种形式:一般式、顶点式、交点式
如图:

二次函数的增减性:当a>0时,对称轴左侧,y随x增大而减小;对称轴右侧,y随x增大而增大
当a<0时,对称轴左侧,y随x增大而增大;对称轴右侧,y随x增大而减小
要注意,开口方向决定上升下降,与对称轴确定
勾画草图的关键点:1.开口方向
2.对称轴
3.顶点
4.和x轴交点
5.和y轴交点
图像平移步骤:(1)配方得到顶点式y=a(x-h)²+k,确定顶点(h,k)
(2)对x轴 左加右减 (括号内);对y轴 上加下减(括号外),借助顶点来进行图像的平移
二次函数的对称性:二次函数是轴对称图形
所以,当横坐标为x1、x2其对应的纵坐标相等,那么对称轴x=x1+x2/2
二次函数的最值:当x=-(b/2a)时,y(最小)=4ac-b²/4a
当x=-(b/2a)时,y(最大)=4ac-b²/4a
第十章:
反比例函数定义:一般我们把如:y=k/x(k≠0,x≠0),称为反比例函数
注:k为常数项
k<0:函数图像在二四象限,在每一个象限内,y随x的增大而增大
k<0:函数图像在一三象限,在每一个象限内,y随x的增大而减小
反比例函数图像:关于原点成中心对称图形
反比例函数的模型:关于比例系数k的几何意义:y=k/x(k≠0,x≠0)
在图像中,任取一点p过这一点向x轴和y轴分别作垂线,p点与坐标轴围成的矩形面积是定值,p(x,y)
此矩形面积=|xy|=k
在图像中,任取一点p过这一点向坐标轴作垂线,p点与垂足以及坐标原点所围成的三角形的面积是定值,p(x,y)
此三角形面积=1/2|xy|=|k|/2
反比例函数模型列:1.在y轴上任取一点B连接PB、AB,则不论P在双曲线上何处,不论B在y轴上何处,三角形PAB的面积始终=|k|/2
2.PAOB为矩形,当OA在x轴上平移时,矩形面积始终=|k|,y轴上亦成立。
3.PQ为双曲线上的点,连接POQ,过PQ向x轴做垂线,垂足为AB,PA交QO于M,则OPQ=PABQ
5.矩形ABOC与双曲线交于PQ,则PQ平行BC,AP/AB=AQ/AC
6.过双曲线上任意一点P、Q做直线,PQ分别交x轴y轴与点A、B,则PB=QA
第十一章:
旋转的定义:三要素:旋转中心、旋转方向和旋转角度
旋转的性质:①旋转前后的图形全等;
②对应点到旋转中心的距离相等;
③对应角与旋转中心所连线段的夹角等于旋转角
答题公式:1.确定旋转三要素
2.找到旋转后的点,进行测量
3.连点成线
中心对称:图形绕一点旋转180度重合,称这两个图形形成中心对称,此图形叫做中心对称图形
(1)点p(x,y)关于x的轴对称点的坐标是(x,-y)
(2)点p(x,y)关于y的轴对称点的坐标是(-x,y)
(3)点p(x,y)关于原点对称点的坐标是(-x,-y)
第十二章:
圆的定义:动态定义:线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图像叫做圆
静态定义:到定点的距离等于定长的点的集合叫做圆
圆中的线:1.弦:圆上任意两点之间的线段
2.直径:经过圆心的弦
3.半径:圆心与圆上任意一点的线段
4.弦心距:从圆心到弦的距离
5.弧:圆上任意两点的部分
6.半圆:直径分成的两条弧
7.优弧:大于半圆的弧
8.劣弧:小于半圆的弧
圆中的角:圆心角:顶角在圆心的角
圆周角:定点在圆上,并且两边都能与圆相交的点
垂径定理:垂直于弦的直径平分弦,并且平分弦对应的两条弧。
圆心角相关定理:在同圆或等圆中,相等的圆心角所对的弧相等,弦也相等。(注意,必须是同圆或等圆)
切线:经过半径外端并且垂直于这条半径的直线为圆的切线
性质:1经过切点的垂线于这条半径的直线是圆的切线
2经过切点垂直于切线的直线必经过圆心
3圆的切线垂直于经过切点的半径
垂径定理:垂直于弦的直径平分弦,并且平分弦所为两条弧。
第十三章:三角函数:
(1)角A 的对边与斜边的比值是角A 的正弦,记作sinA=角A 对边/斜边
(2) 角A 的邻边与斜边的比值是角A 的余弦,记作cosA=角A 邻边/斜边
(3) 角A 的对边与邻边的比值是角A 的正切,记作tanA=角A 对边/邻边
特殊值
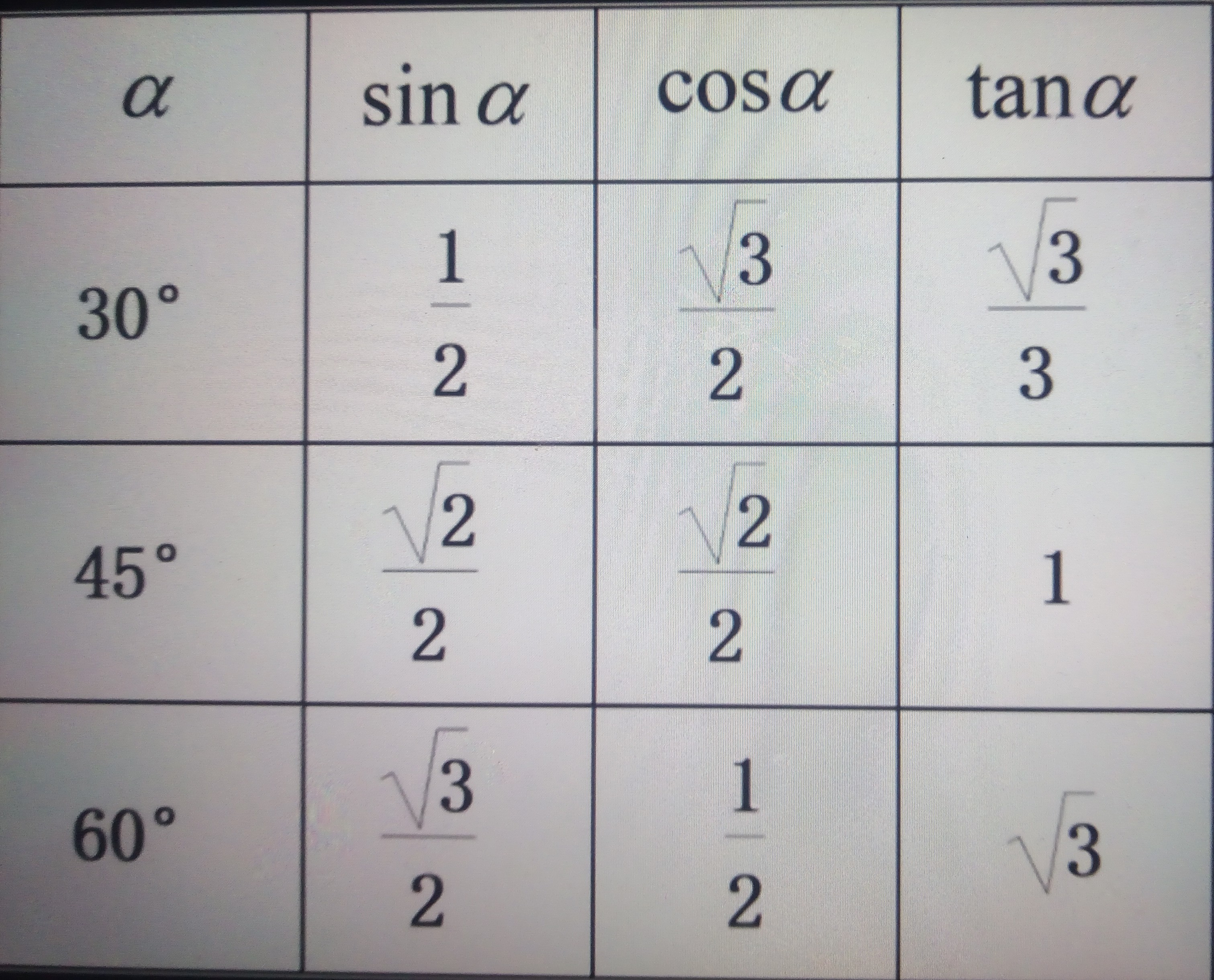
第十四章:统计与概率
比较简单1,dy搜一下就能会
完结,事后会有新的整理,不见不散
