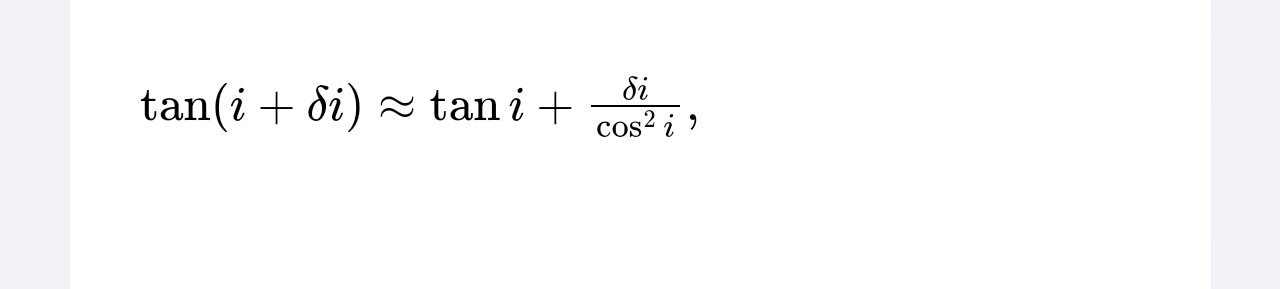物理

小量近似怎么证明

哦哦，刚才图没贴上去🤔

$\tan(i + \delta i) \approx \tan i + \dfrac{\delta i}{\cos^2i}$

帖主忘加💲了吧？

是不是光学题里看到的

大佬好牛。

直接泰勒展开一阶一步到位不是更方便吗@Ashley

求教tan怎么泰勒展开？

泰勒展开的形式你应该知道的吧（不知道可以去查一下，懒的打了）。tan 的一阶导不就是cos的负二次方吗。然后代到泰勒展开的公式里不就好了嘛。这里显然是展开到一阶。如果求导不知道咋折腾，可以去稍微学一下求导，学了毕竟也几乎没有坏处。

大佬我还是不理解。泰勒展开tan哪有cos啊？

泰勒展开的在f(x＋Delta x)在x处形式是f(x)+f(x)的一阶导乘Delta x加f(x)的二阶导除以2的阶乘以此类推。tan的一阶导等于sin／cos 的一阶导是显然的，sin 的导是cos，cos 的导是负sin。(a/b)的导，ab各为一个函数，等于a的导乘b减去b的导乘a整个除以b的平方。那么tan的导就等于cos方加sin 方除以cos 方，其中cos 方加sin 方等于一（这总不用我说了吧），那么就能得到tan的导等于cos 的负二次方。（整个过程中的三角函数懒的打变量了，反正是同一个变量）这里显然是在i处展开，那么带进去就是tan i＋i后面那一堆／cos i的平方。这里很显然带进去是一阶近似，要写还是能往后写的，所以我也不知恒等是怎么变出来直接画等号的。

都说这么多了导函数也就是某一个函数的切线函数。f(x)的导函数为f(x+dx)-f(x)/dx,其中dx为x的微元，也可以理解为就是很小的量，为一阶无穷小，在化简包含无穷小的时候二阶对一阶为零，更常见，更高阶的无穷小量在低阶无穷小量面前可当作零处理，无穷大则简单说相反。sin cos 的导代公式再稍微处理一下就很好得结果我就不说了

懂了，之前以为泰勒展开式都是麦克劳林展开，不知道有在x0附近的泰勒展开式

，现在明白了，感谢你耐心指点