共11条回复
时间正序
1条评论
- 1
4条评论
破晓时分
10月前
小蓝本哪一册
Yuki
10月前
答案是[1，1.5）并[2，+∞）
Yuki 回复 破晓时分
10月前
函数与函数方程，我记得位置很靠前
破晓时分 回复 Yuki
10月前
谢谢佬了
永不停息的简谐振动
10月前
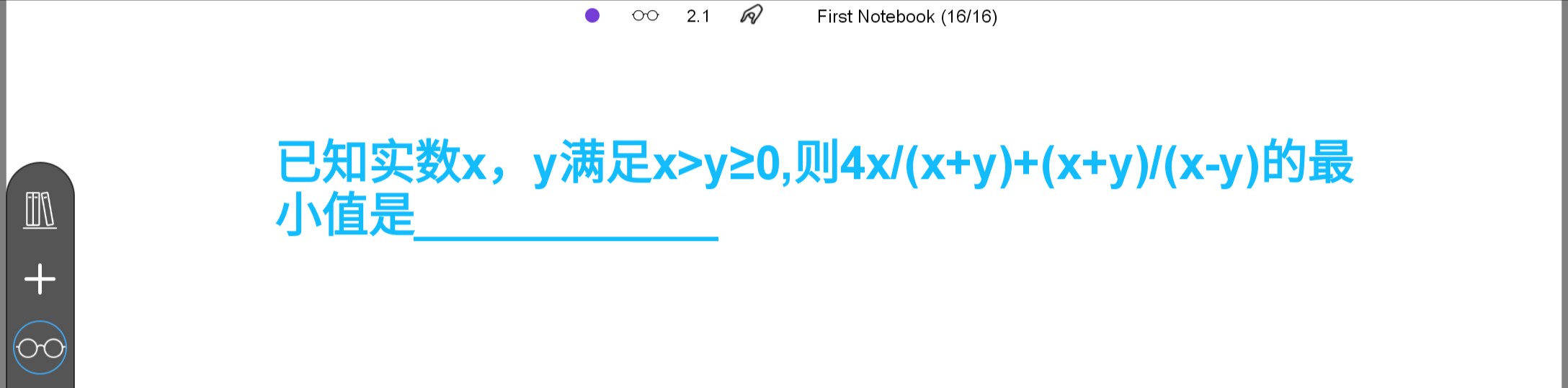
$由于要采用基本不等式解决$
$故要把不和谐的式子\dfrac{4x}{x + y}转化为合适的样子$
$也就是用x+y和x-y来表示(待定系数)$
$即：$
$令4x = \lambda(x + y) + \mu(x - y)$
$\therefore 4x = (\lambda + \mu)x + (\lambda - \mu)y$
$\Rightarrow \begin{cases}{\lambda + \mu = 4}\\{\lambda - \mu = 0}\end{cases}$
$解得，\begin{cases}{\lambda = 2}\\{\mu = 2}\end{cases}$
$\therefore 4x = 2(x + y) + 2(x - y)$
$原式 = \dfrac{2(x + y) + 2(x - y)}{x + y} + \dfrac{x + y}{x - y}$
$ = \dfrac{2(x - y)}{x + y} + \dfrac{x + y}{x - y} + 2$
$由于基本不等式条件是两代数式为正，故需验证$
$\because x \gt y \geqslant 0$
$\therefore x + y \gt x - y \gt 0$
$因此可以用$
$\therefore 原式 \geqslant 2 + 2\sqrt{\dfrac{2(x - y)}{x + y} + \dfrac{x + y}{x - y}}$
$ = 2 + 2\sqrt2$
$当且仅当\dfrac{2(x - y)}{x + y} ＝ \dfrac{x + y}{x - y}$
$即x = (3 + 2\sqrt2)y时取等号$
，你是把作业全部拍上来了吧🤣5条评论
破晓时分
8月前
一堆不会啊😱
Cx330 回复 破晓时分
8月前
坚强的数竟生是不会被学校的题目给打倒的
。你们老师有没有说这是啥难度的？
破晓时分 回复 Cx330
8月前
没说啊，给我做废了，我作业还有一堆
破晓时分 回复 破晓时分
8月前
我第十四题才做出来了
热情的广天 回复 破晓时分
8月前
看到这里我于是不敢说我学了基础轮。😅
