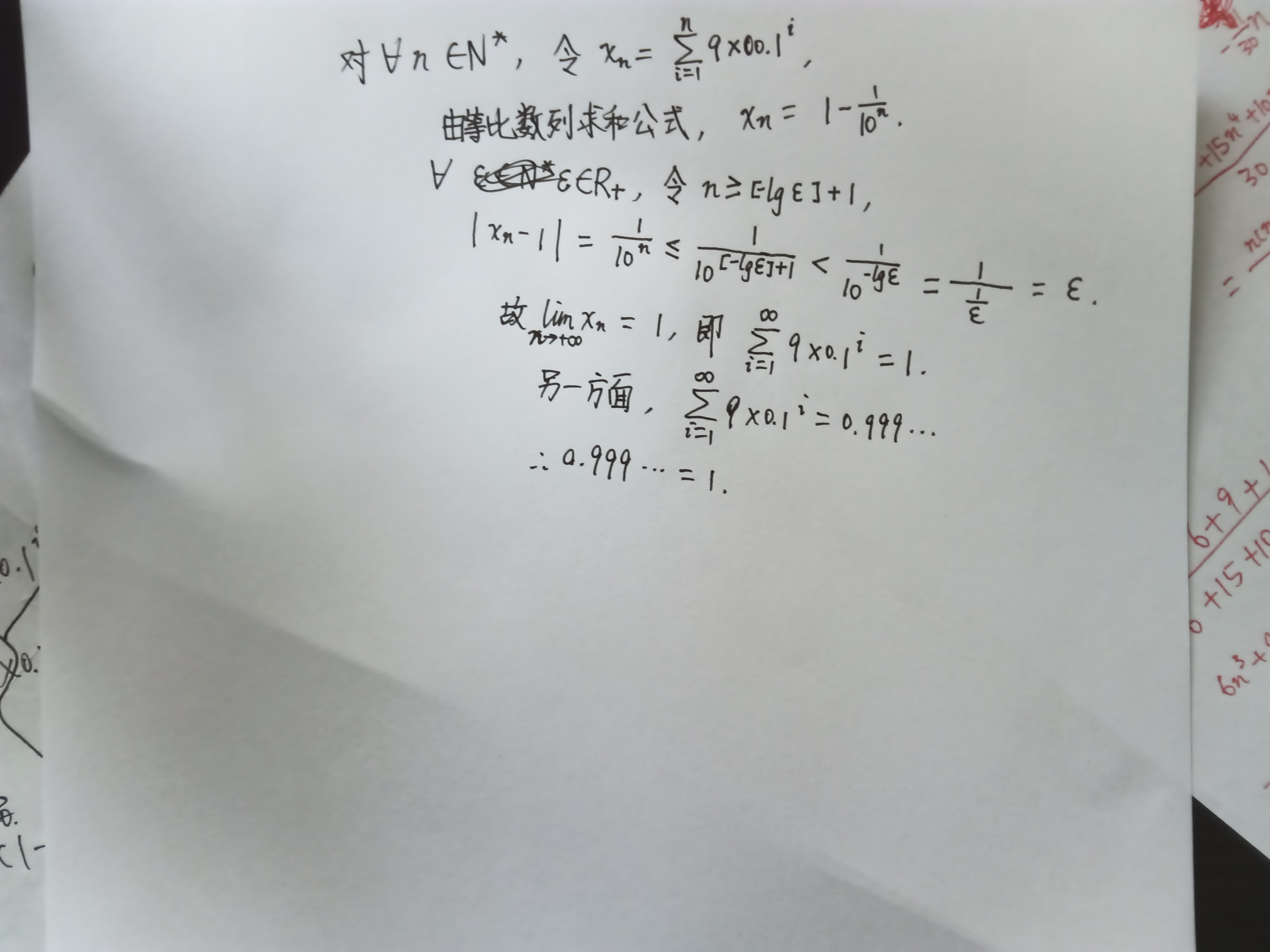共10条回复
时间正序
1条评论
- 1
.
10月前
令a=0.999...,b=1, 若存在一x∈(0,1)使a<x<b,则a<b。由于对于每一个小数位，9始终为较大数，即满足要求的x不存在。由反证法可得，a<b不成立，即a≧b。而a>b显然不成立，由排除法可得a=b
4条评论
K
10月前
- 令a=0.999999......
- 则10a=9.999999......
- 9a=10a-a=9 即a=9/9=1
. 回复 K
10月前
附议。
天贶#论坛已删 回复 K
10月前
无穷级数不能随意加减，容易循环论证。
ricky 回复 K
10月前
这种证明是不对的，不然我说S=1+1+1+.......=1+1+(1+1+1+.....)
得1+1+～S=S，2=0
这显然是荒谬的
阿尔伯特.爱因斯坦
10月前
根据有理数的稠密性，两个不相等的有理数间一定还有有理数。
在数轴上0.9999999999...无限接近1，要在其中找到一个有理数既不＝0.99999999...，又不＝1，这是一个不可能的事。
这违反了有理数的稠密性，相当于数轴断开了。
所以0.9999999999...=1
