共4条回复
时间正序
2条评论
- 1
永不停息的简谐振动
10月前
复杂预警！！！
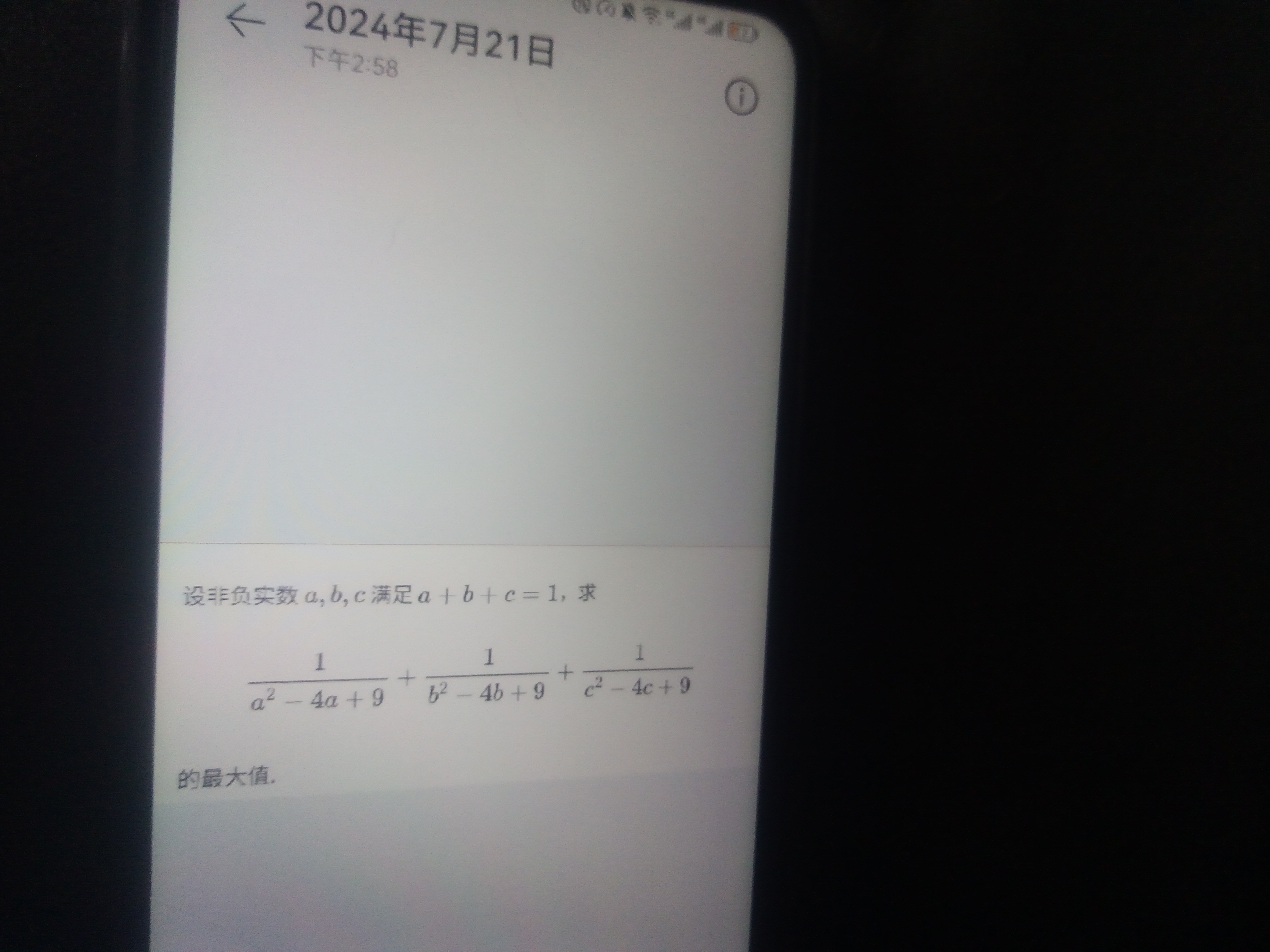
由于要求最值的三个式子长得挺相似 那么先换个元分析再说
$\because 实数a,b,c \geqslant 0$
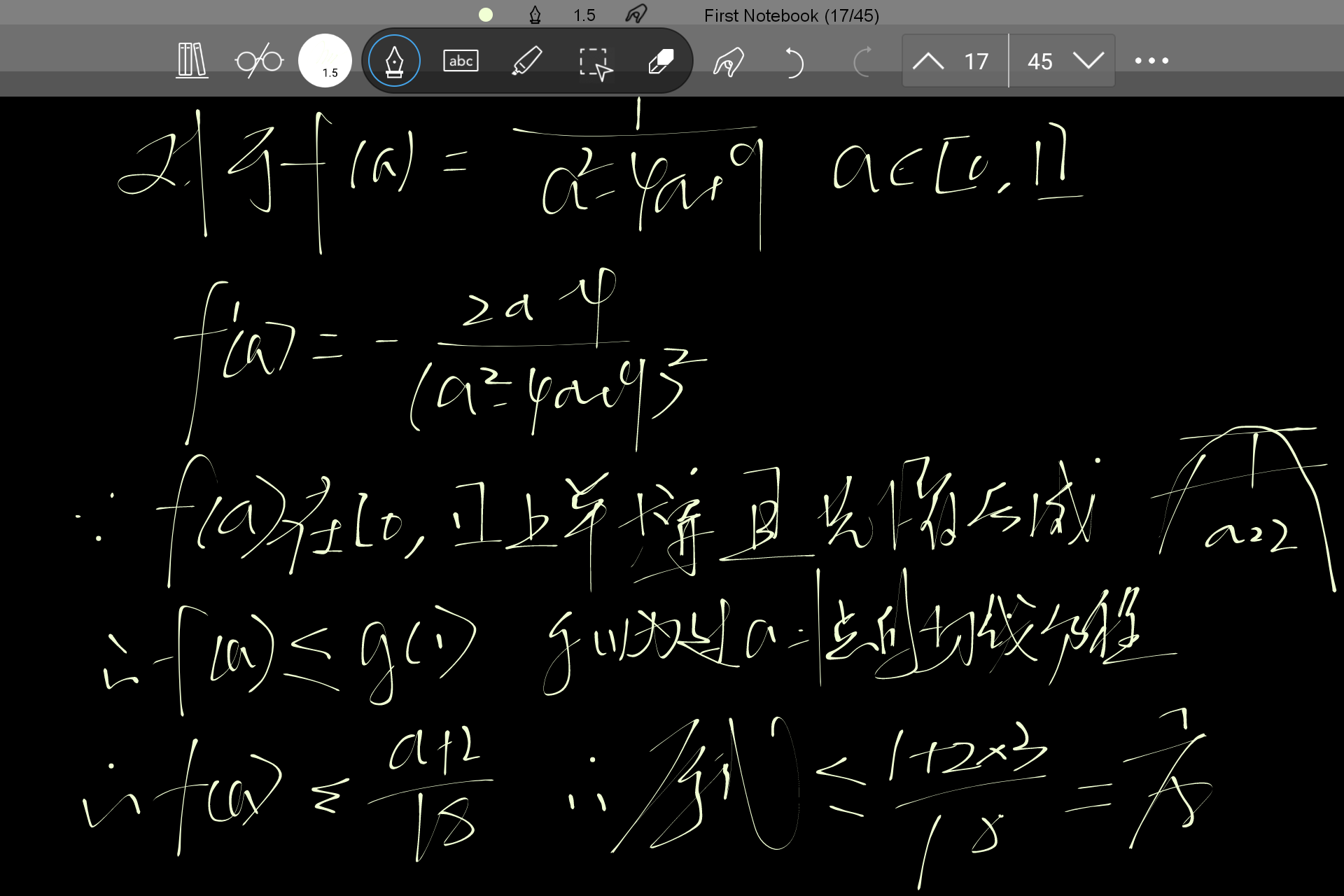
$令f(x)=\dfrac{1}{x^2-4x+9}$
$\therefore f'(x)=-\dfrac{2x-4}{{(x^2-4x+9)}^2}$
$\Rightarrow f'(1)=\dfrac{1}{18}$
然后逆向思考一下 即假设$f(x)-f'(1)\leqslant f'(1)\cdot(x-1)=\dfrac{1}{18}(x-1)$
接下来只要证明假设再代入原式就能求解
但正面不好证 由此想到逆推
$\because 原式 \Leftrightarrow \dfrac{18}{x+2} \leqslant x^2-4x+9$
整理得到一元三次不等式 因式分解，得：
$x{(x-1)}^2 \geqslant 0$
其在$x \in [0,1]$时明显成立
猜想得证！
推广到$a，b，c$
$\therefore 原式 \leqslant \dfrac{7}{18}$
$"=''在一个数取1另两数取0时可取到$
不知道对不对。。。望大佬指正！
3条评论
天贶#论坛已删
10月前
咱俩方法好像差不多唉
不过那个假设应该不用那么复杂，本质就是切线方程嘛，函数先增后减，所以就是小于等于a=1处的切线方程，直接列即可（吧）
永不停息的简谐振动 回复 天贶#论坛已删
10月前
确实
。
Issac Liuton 回复 永不停息的简谐振动
10月前
比我的方法好，我的方法刚才发现还有漏洞🤣
