物理

优雅，太优雅了！！！

一道数学题

现有一个三维球体，在球面上任意取四点P₁、P₂、P₃、P₄，连接这四点构成一四面体，求球心落在四面体内部的概率

PS:一道在b站找到的数学题，思路的引入自然且优美，奇妙至极，解法极其优雅，快来做罢！

思路与解法：

对于本题，先考虑二维情况，若确定两点P₁、P₂则当点P₃位于P₁P₂关于圆心对称的弧上时圆心位于△P₁P₂P₃内，由于圆心角∠P₁OP₂∈(0°,180°)，则可知其平均概率为P=0.5×(0+0.5)=0.25,如下图

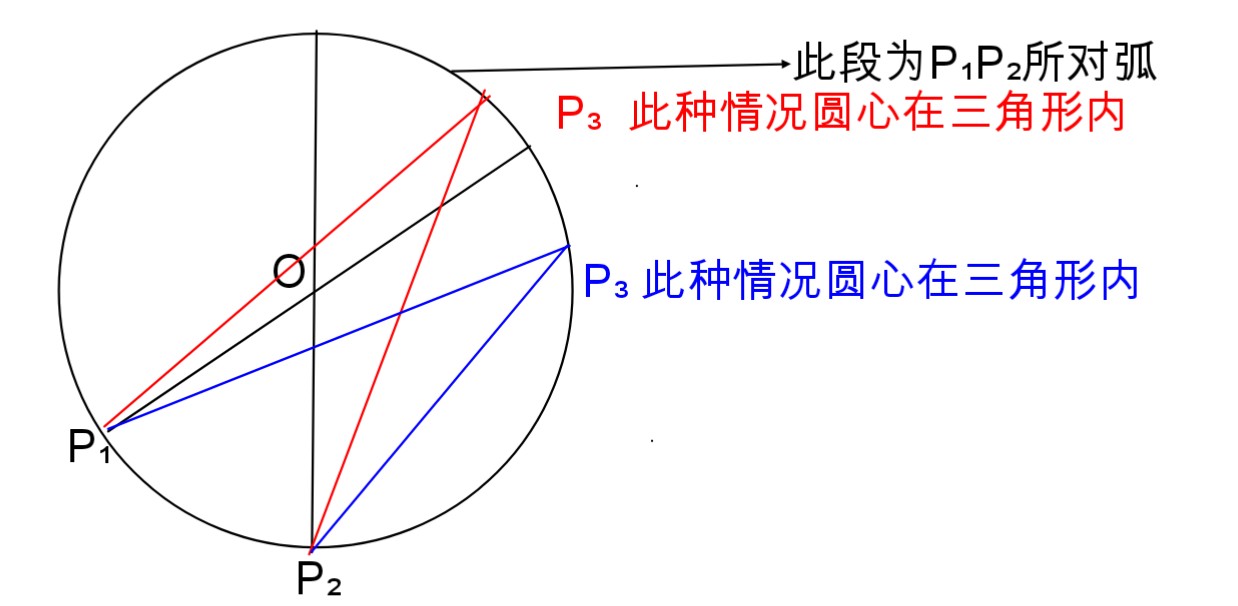
再将问题拓展至三维球体中考虑，可发现需考虑球体上一曲面说对的面积，可尝试曲面积分但过于复杂故舍去，重新回到二维圆中考虑

接下来考虑上述思考中添出的两处辅助线具有何种意义，设两条线段与圆的交点分为A,B,C,D，现更改定点为P₃，P₁,P₂仅可取ABCD中两点，选取共有四种情况，仅有P₁,P₂与P₃位于所作辅助线两侧时圆心位于△P₁P₂P₃内，概率P=0.25，重新回到三维球体中考虑

过球心O作三条不重叠的直线，设其交点分为A,B,C,D,E,F，但P₁,P₂,P₃选取其中任意三点时共有八种情况，其中亦仅有一种使得P₁,P₂,P₃位于所作辅助线两侧，易得本题所求概率P=0.125

附加题：

试证明推论：在x维超球内，球心位于由P₁……Pₓ₊₁构成超几何体内的概率P=1/2ˣ.