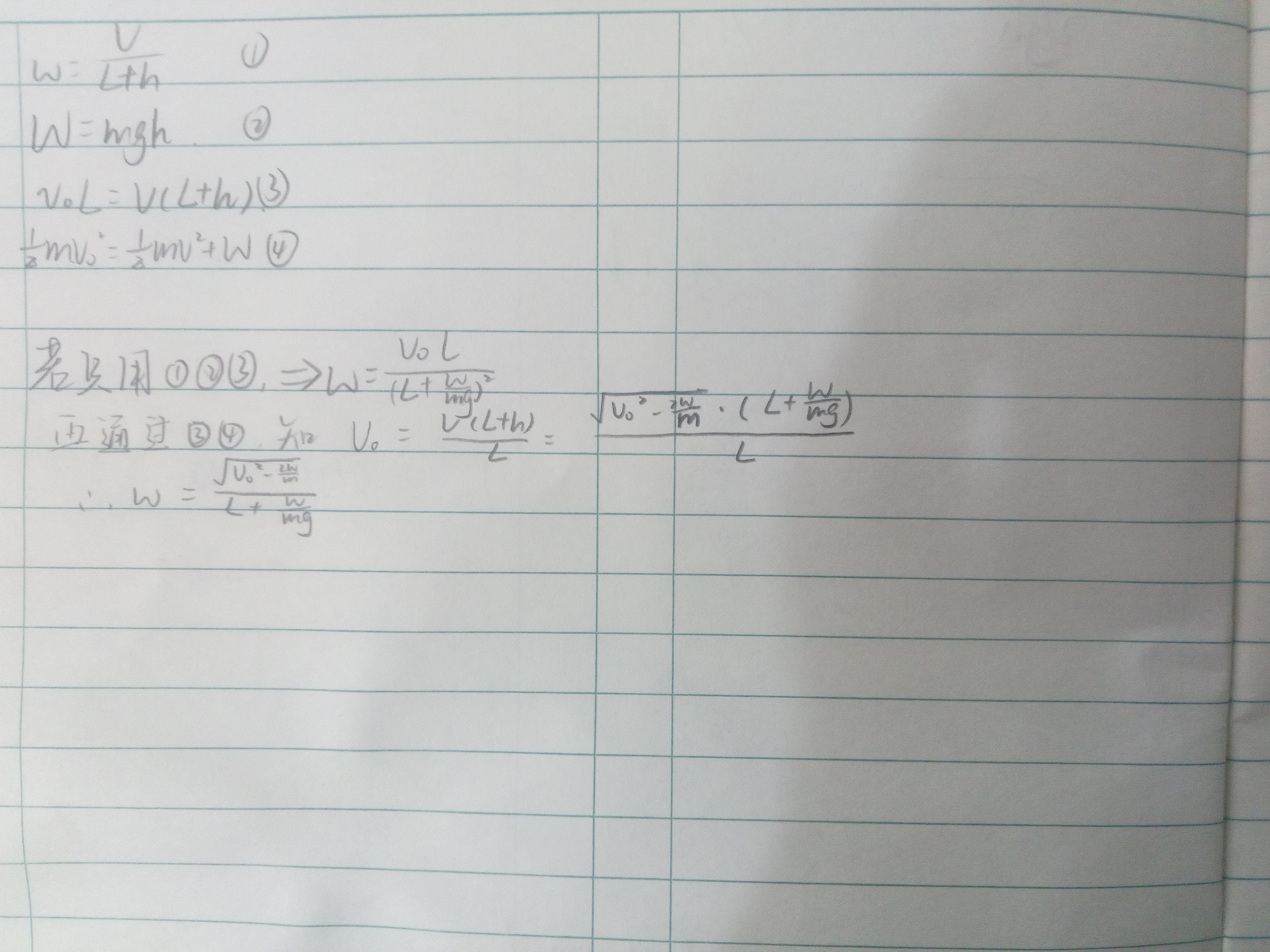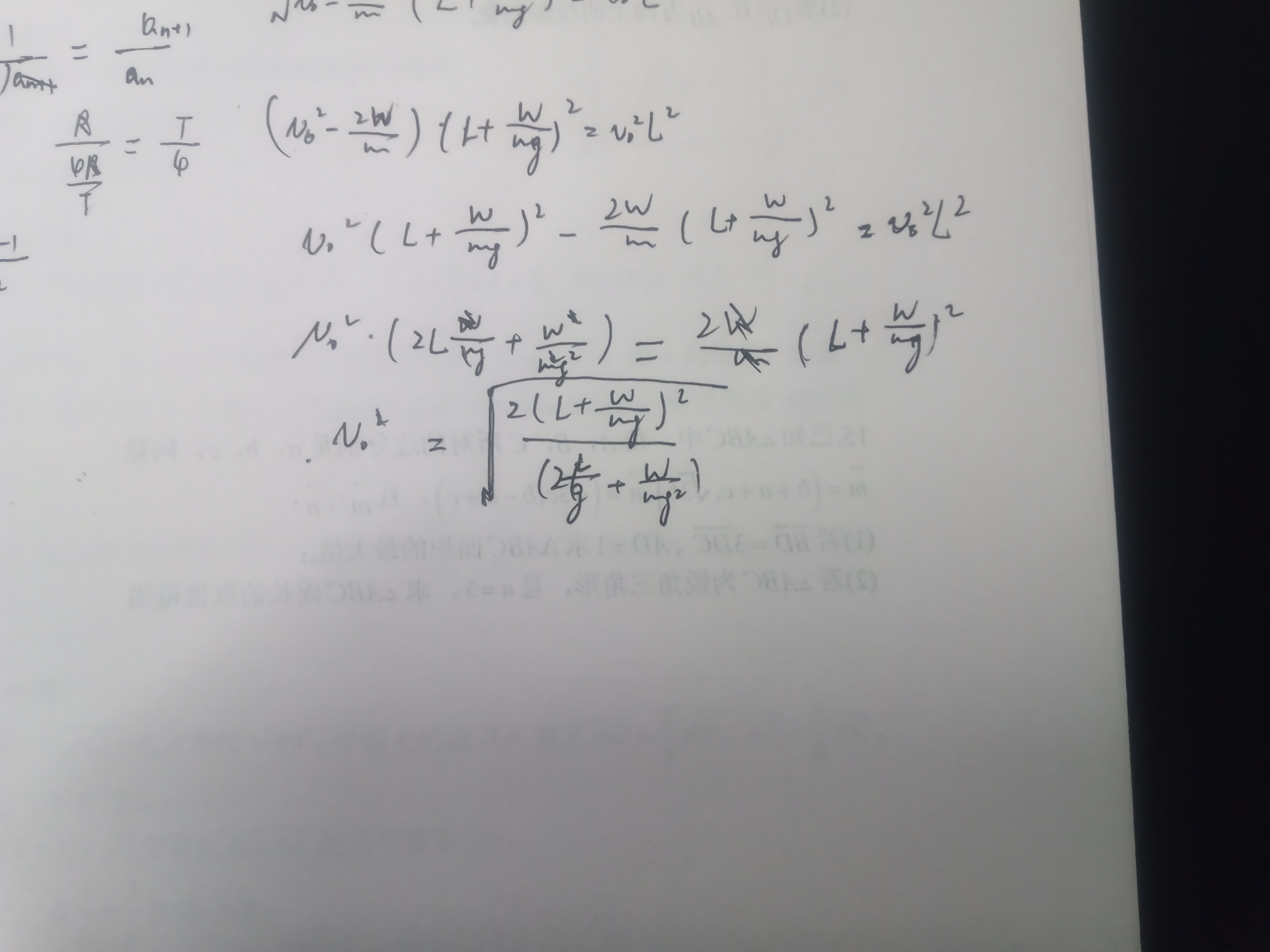众所周知，我们的学习是要循序渐进的，不可能跳过高中物理直接学物理竞赛。而为了更好地学习高中物理，我们需要做很多高中物理的题目，其中不乏有一些易错题，甚至有人第一次做错了，第二次还是错。但是当我们学了物理竞赛之后，就会发现，在高中物理看来容易做错的题，用了竞赛方法简直就是送分题。于是我们开始用竞赛方法解高中物理题。结果，原先做错的题做对了，原先做对的题却做错了。但只要我们仔细分析一下做错的原因，就会发现，真正做错的不是我们，而是高中物理的题目本身。但我们又不得不要在高中物理的考试中获得分数，所以我们又只能按照高中物理的方法来解。有时候，高中方法会令我们一知半解，不知道高中方法为什么是对的（这也许是我学物理竞赛的原因之一吧），这时候，一些没有超出高中太多的竞赛方法，在最终答案正确的前提下也能得分，但如果在解答题出现了超出高中太多的竞赛方法，即使最终答案正确也会扣分。

所以，至于要不要用竞赛方法解高中物理题，我的观点是：如果用高中方法能做对，考试的时候就不要用竞赛方法做，而平时可以用竞赛方法来训练思维，并分析高中方法与竞赛方法算出来结果不一样的原因，从而对物理有更深入的理解。但如果你把某道高中物理题做错了（不包括基础知识遗忘、审题不清、计算出错等，而是你真的把它做错了，而且很多人都也做错了），你就可以用竞赛方法把它再做一遍，以后碰到类似的题，也可以用竞赛方法做（但是也很难碰到类似的题了）。

那么，我们要如何用竞赛方法解高中物理题呢？光说不做是不行的，所以我们通过4道例题来详细讲解高中物理题的高中解法和竞赛解法，其中前2道对于高中物理来说是易错题，第3道属于高中方法和竞赛方法都能做的题，第4道则是用高中方法能做对、用竞赛方法就会做错的题。至于标题为什么多了“易错”二字，一是值得用竞赛方法解的高中物理题主要是易错题，二是希望你们如果遇到高中物理的易错题也可以在评论区补充。

例1  相对运动（易错题）

（这篇帖子）

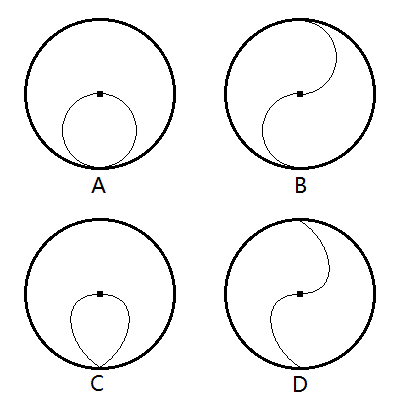
半径为R的光滑水平玻璃圆桌以周期T匀速转动，一小球从桌边对准圆心以速度$v=\dfrac{4R}{T}$匀速通过桌面，则小球在桌面留下的痕迹可能是

错解1：（高中解法）（错误原因：凭感觉做题）

小球通过桌面的时间 $t=\dfrac{2R}{v}​=\dfrac{T}{2}$​，感觉运动了半圈，排除AC

B和D感觉B的轨迹更美，选B

（理科千万不要凭感觉做题！！！文科可以）

错解2：（高中解法）（错误原因：相对运动考虑不清楚）

小球通过桌面的时间 $t=\dfrac{2R}{v}​=\dfrac{T}{2}$​，桌面转了180°，排除AC

小球通过桌面边缘时，小球速度沿半径方向，桌边速度垂直半径方向，相对速度就与半径成一定夹角，排除B，选D

（桌面转了180°，小球呢？）

正解1：（高中解法）

小球通过桌面的时间 $t=\dfrac{2R}{v}​=\dfrac{T}{2}$​​，桌面转了180°，小球从一边运动到另一边，也相当于转了180°，所以​小球与桌面边缘的两交点重合，排除BD

小球通过桌面边缘时，小球速度沿半径方向，桌边速度垂直半径方向，相对速度就与半径成一定夹角，排除A，选C

正解2：（竞赛解法——极坐标系）

设小球通过圆心时t=0，圆桌逆时针转动，小球相对地面的轨迹是一条直线，则这条直线相对圆桌顺时针转动，角速度为 $\omega=\dfrac{2\pi}{T}$

小球相对圆桌的极坐标方程为$\begin{cases}r=vt\\\theta=-\omega t\end{cases}$

消去t，得$\theta=-\dfrac{\omega r}{v}=-\dfrac{\pi}{2}\cdot\dfrac{r}{R}$

作图，注意r<0时对应的点在θ的反方向，选C

例2  碰撞（易错题）

（原题找不到了，所以自己出一道）

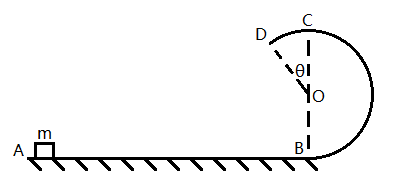
一游戏装置如图所示，该装置由粗糙直轨道AB和光滑圆弧轨道BCD组成，两轨道在B点相切，整个装置固定在光滑水平面上（题图为俯视图）。轨道AB的长度为L=4R，光滑圆弧轨道的半径为R，BC为直径，OC与OD的夹角为θ=37°。将一质量为m的滑块（可视为质点）放在A点，并使其获得沿AB方向的初速度v，滑块与AB的动摩擦因数为μ=0.5。滑块沿轨道内侧运动到D点，而后飞出轨道，一段时间后与轨道AB发生完全非弹性碰撞，碰撞后滑块沿BA方向运动，并回到A点。（sin37°=0.6, cos37°=0.8）

(1)求滑块经过C点时对轨道的压力

(2)求滑块回到A点时的速度大小

错解1：（高中解法）（错误原因：审题不清、“牛三”不规范）

(1)

根据动能定理  A→C

$-\mu mgL-2mgR=\frac{1}{2}mv_C^2-\frac{1}{2}mv^2$

$\Rightarrow v_C^{}=\sqrt{v^2-8gR}$

$F_N+mg=m\dfrac{v_C^2}{R}$

$\Rightarrow F_N=m\dfrac{v^2}{R}-9mg$

根据牛三  $F_N'=F_N=m\dfrac{v^2}{R}-9mg$    竖直向上

（题目都说了，整个装置固定在光滑水平面上（题图为俯视图），你怎么就没看到呢？是不是看到图就开始做题了？）

（还有，“根据牛顿第三定律”千万不要为了省时间简写成“根据牛三”，会扣分的！）

错解2：（高中解法）（错误原因：忽略摩擦力的冲量）

(2)（前面同正解1）

问题简化为求碰后速度与碰前速度的关系

完全非弹性碰撞，法向速度变为0

碰撞时间很短，摩擦力的冲量可以忽略，切向速度不变

$v'=v\cos\theta=\frac{4}{5}v$

（摩擦力的冲量真的可以忽略吗？要是摩擦力很大呢？而且，一道题有可能这么简单吗？）

正解1：（高中解法）

(1)

AB段，滑块与AB没有力的作用，水平面光滑，v不变

BCD段，水平面和BCD都光滑，v不变

$F_N=m\dfrac{v_C^2}{R}=m\dfrac{v^2}{R}$

根据牛顿第三定律  $F_N'=F_N=m\dfrac{v^2}{R}$    $\overrightarrow{OC}$方向

(2)

滑块从D点飞出轨道后做匀速直线运动，设D点切线交AB于E

∠DEB=θ，OE平分∠DEB，则$\tan∠OEB=\tan\dfrac{\theta}{2}=\dfrac{1}{3}$

∴BE=3R<L，E点在线段AB上，滑块与AB在E点碰撞

碰后，滑块与AB没有力的作用，水平面光滑，速度不变

问题简化为求碰后速度与碰前速度的关系

设碰撞时间为$\Delta t$，假设碰撞过程中始终有相对滑动（若v'>0，则假设成立）

完全非弹性碰撞，法向速度变为0

$\overline{F_N}\Delta t=mv\sin\theta$

$\overline{f}=\mu\overline{F_N}$

$-\overline{f}\Delta t=mv'-mv\cos\theta$

$\Rightarrow v'=\frac{1}{2}v$

正解2：（竞赛解法——微积分）

(2)（前面同正解1）

问题简化为求碰后速度与碰前速度的关系

设碰撞时间为$\Delta t$，假设碰撞过程中始终有相对滑动（若v'>0，则假设成立）

完全非弹性碰撞，法向速度变为0

$\int_0^{\Delta t}F_N\mathrm{d}t=mv\sin\theta$

$f=\mu F_N$

$\int_0^{\Delta t}f\mathrm{d}t=\int_0^{\Delta t}\mu F_N\mathrm{d}t=\mu\int_0^{\Delta t}F_N\mathrm{d}t$

$-\int_0^{\Delta t}f\mathrm{d}t=mv'-mv\cos\theta$

$\Rightarrow v'=\frac{1}{2}v$

正解3：（竞赛解法——全反力）

(2)（前面同正解1）

问题简化为求碰后速度与碰前速度的关系

假设碰撞过程中始终有相对滑动（若v'>0，则假设成立）

完全非弹性碰撞，法向速度变为0

$f=\mu F_N$    $\Rightarrow\dfrac{f}{F_N}=\mu=\dfrac{1}{2}$

设全反力的方向与法线的夹角为$\varphi$，则$\tan\varphi=\frac{1}{2}$

全反力的冲量与全反力同向

$\vec{I}=m\vec{v}'-m\vec{v}$

$\begin{cases}I\cos\varphi=mv\sin\theta\\-I\sin\varphi=mv'-mv\cos\theta\end{cases}$

$\Rightarrow v'=\frac{1}{2}v$

例3  磁聚焦

（这篇帖子改编）

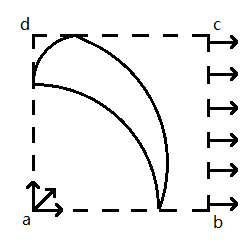
如图，正方形abcd的边长为L，a点处有粒子源，可以向正方形abcd所在区域的任意方向发射速率为v、质量为m、电荷量为+q的粒子。在物理课上，老师要求学生们在正方形abcd内设计一个区域，在该区域内存在着方向垂直纸面的匀强磁场，使得所有粒子均垂直bc边射出，bc边上的任意一点均有粒子射出，且该区域的面积尽可能小。于是我运用某高考模拟卷的磁聚焦模型，设计了如图所示的区域，该区域由3段圆弧围成，左下方的圆弧圆心为a点，半径为R；左上方的圆弧与ad、cd相切，半径为r；右上方的圆弧圆心在ad上与a点距离为r，半径为$\sqrt{R^2+r^2}$，且满足$R+r=L$ 。

(1)证明我设计的区域符合题意

(2)求我设计的区域的面积与磁感应强度的关系

正解1：（高中解法）

(1)

粒子在磁场中运动的半径为r

粒子运动到左下方的圆弧，刚进入磁场时，半径与运动轨迹切线垂直，即与左下方的圆弧相切

所以粒子运动轨迹的圆心在以a为圆心、半径为$\sqrt{R^2+r^2}$的圆上，恰好为右上方的圆弧向下平移r

所以粒子在磁场中的轨迹圆与右上方的圆弧的交点恰好在轨迹圆心上方r处

所以粒子出磁场时，运动方向与bc垂直

(2)

先考虑右上方的圆弧，连接圆弧端点与圆心，得到圆心角90°的扇形，面积$\dfrac{\pi}{4}(R^2+r^2)$

然后挖去一个直角三角形（顶点(0,r),(r,r),(r,L) ），填到左下方，面积不变

最后补上(R-r)×r的长方形、半径为r的圆弧，挖去半径为R的圆弧

$S=\dfrac{\pi}{4}(R^2+r^2)+(R-r)r+\dfrac{\pi}{4}r^2-\dfrac{\pi}{4}R^2=Lr-(2-\dfrac{\pi}{2})r^2$    $(r\le L)$

$qvB=m\dfrac{v^2}{r}$

$\Rightarrow S=\dfrac{mvL}{qB}-(2-\dfrac{\pi}{2})(\dfrac{mv}{qB})^2$    $(B\ge\dfrac{mv}{qL})$

正解2：（竞赛解法——角动量）

(1)

$\mathrm{d}L=qv_rB\mathrm{d}t\cdot r_a=qBr_a\mathrm{d}r_a$

$L=\int_R^{r_a}qBr_a\mathrm{d}r_a=\frac12qB(r_a^2-R^2)$

设粒子从(x,y)离开磁场

$x^2+(y-r)^2=R^2+r^2$

$r_a^2=x^2+y^2$

$qvB=m\dfrac{v^2}{r}$

$\Rightarrow L=\frac12qB[y^2+r^2-(y-r)^2]=qBry=mvy$

所以粒子离开磁场后的轨迹直线到a的距离为y，又粒子是向右偏转的，所以粒子出磁场时，运动方向与bc垂直

(2)

（同正解1）

例4  圆周运动

（这篇帖子）

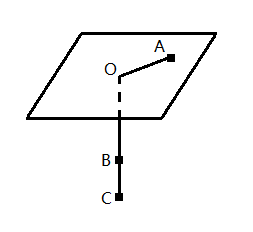
如图，足够大的光滑板固定在水平面内，板上开有光滑的小孔O，细线穿过小孔，将小球A,B,C拴接。小球A在光滑板上做匀速圆周运动，小球B,C自然下垂处于静止状态。已知小球A,B,C的质量均为m，小球A到小孔O的距离为L，重力加速度为g。

(1)求小球A做圆周运动的速度大小$v_0$

(2)剪断B,C间细线后，小球B运动到最高点的过程中（未与板接触），细线对小球B做的功为W，求小球B运动到最高点时小球A的角速度大小ω

正解：（高中解法）

(1)

$2mg=m\dfrac{v_0^2}{L}$    $\Rightarrow v_0=\sqrt{2gL}$

(2)

$ω=\dfrac{v}{L+h}$​

$W=mgh$

能量守恒 $\frac{1}{2}mv_0^2=\frac{1}{2}mv^2+mgh$

$\Rightarrowω=\dfrac{\sqrt{v_0^2-\frac{2W}{m}}}{L+\frac{W}{mg}}$

错解：（竞赛解法——角动量）

(2)

$ω=\dfrac{v}{L+h}$​

$W=mgh$

角动量守恒 $v_0L=v(L+h)$

$\Rightarrowω=\dfrac{v_0L}{(L+\frac{W}{mg})^2}$

（再加上正解的能量守恒，就是三个未知量$ω,v,h$，四个方程，选择不同的三个方程求解，会得到不同的结果）

（对于高考题，角动量守恒不能用，所以选择正解的三个方程）

（高考题不能用竞赛方法，最主要的原因是高考题会多给条件！）

（如果把题目中的W去掉，就有四个未知量，四个方程，就是一道竞赛题）

改编题：（竞赛解法——角动量）（将W改为未知）

(2)

$ω=\dfrac{v}{L+h}$​

$W=mgh$

能量守恒 $\frac{1}{2}mv_0^2=\frac{1}{2}mv^2+mgh$

角动量守恒 $v_0L=v(L+h)$

$\Rightarrow v^3-(v_0^2+2gL)v+2gv_0L=0$

因为出现了关于v的一元三次方程，所以这里给出数据：$\begin{cases}m=1~\mathrm{kg}\\g=10~\mathrm{m/s^2}\\L=1.8~\mathrm{m}\\v_0=5~\mathrm{m/s}\end{cases}$

$v^3-61v+180=0$

解得 $v=4$ 或 $5$(舍去) 或 $-9$(舍去)

$v=4$ m/s

$h=0.45$ m

$W=4.5$ J

$ω=\dfrac{16}{9}$ rad/s