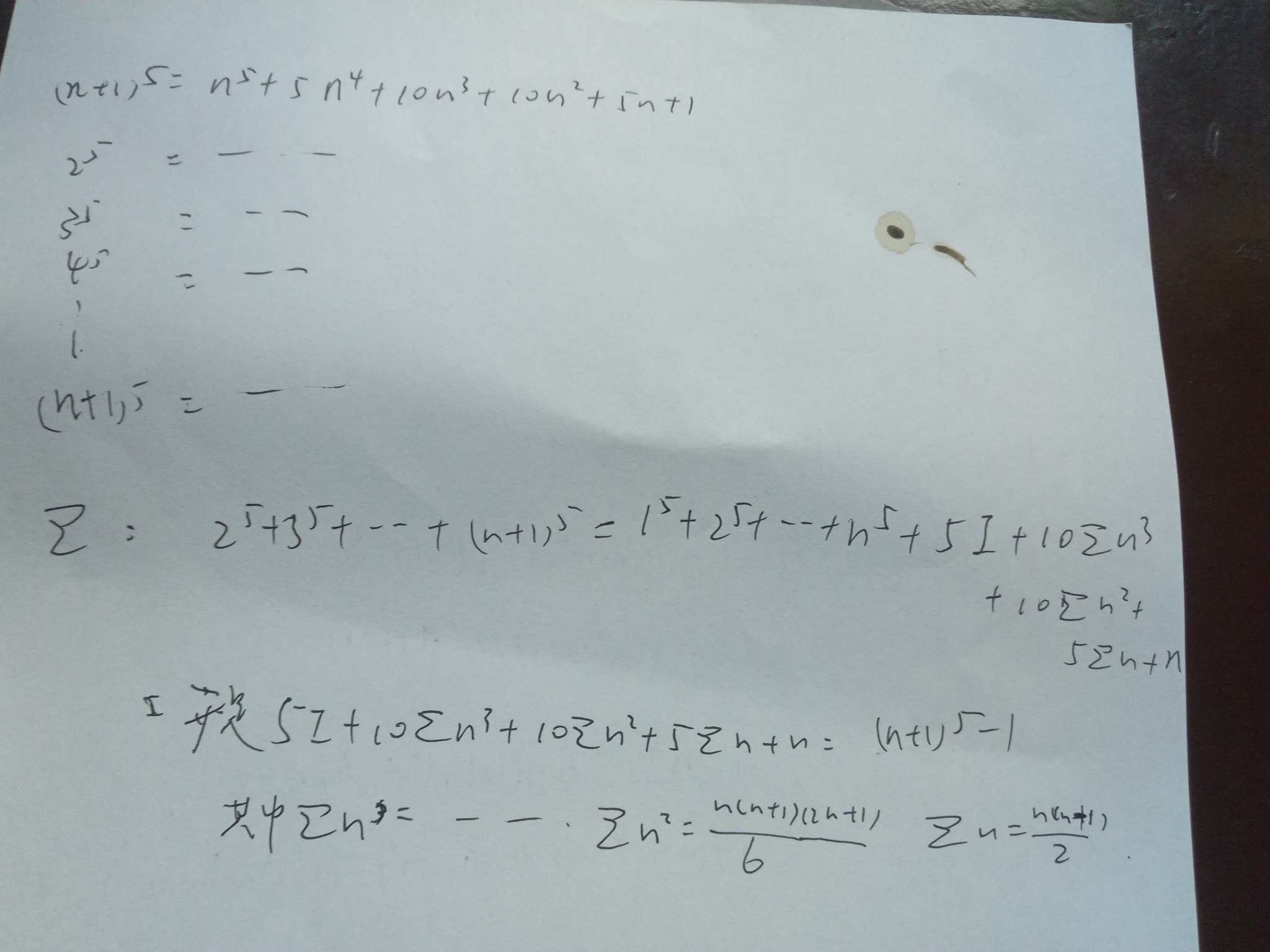四次方求和

数学
四次方求和

用户头像
 Beijing subway 更新于2025-2-14 10:55:22
有没有大佬会1^4+2^4+3^4+...+n^4
收起
5
0
共14条回复
时间正序
用户头像
质心用户 2048
10月前

连续n项自然数的i次方求和是有公式的，具体忘了

另外还有一个可以证明的是连续n项自然数的次方求和必然是一个(i＋1)次多项式

3条评论
用户头像
Beijing subway
10月前

是的，

用户头像
HAWK
10月前

这个关于i与n的通项目前还没找到吧，但每一步都可以通过裂项算出来

用户头像
AE86 回复 Beijing subway
2月前

没这个公式

用户头像
......
10月前
这种公式，搜百度是非常好的选择
用户头像
即未新用户8848114514
10月前
我记得阿贝尔变换是可以解决这些求和问题的，具体怎么解忘记了
4条评论
用户头像
......
10月前

应该没必要吧，我记得裂项（这初中的方法jj-huazhongdian甚至裂项好像根本不算竞赛方法）就行了啊zx-caizixing2@2x，要是我没学到假的数学的话。

用户头像
即未新用户8848114514 回复 ......
10月前

所以这个应该怎么裂项，我看不出来……

用户头像
...... 回复 即未新用户8848114514
10月前

抱歉鄙人今年刚学整式裂项已经忘光了（惭愧实在惭愧，我这数竞像或者说就是白学了一样），建议搜一下zx-sunpeng1@2x

用户头像
...... 回复 即未新用户8848114514
10月前

我有点印象好像是变成i^4=（i+1)^2*(i-1)^2+2i^2-1这类具体的佬可以再试试，,分别再裂然后累加再求合，我就提供个思路，具体操作实在记不起了，佬们可以试试。

用户头像
即未用户8929
10月前
  • 你可以从2022年讲数列的一试课里看到，这大概要用到大学的伯努利数还是什么的，用高中的方法，就是模仿一次二次三次的配凑？没尝试，不确定
用户头像
凡
10月前
x⁴=x（x-1）（x-2）（x-3）+6x（x-1）（x-2）+7x（x-1）+x
然后求和
1条评论
用户头像
......
10月前

这样好像比较烦吧，有个偷懒一点的还是尽量凑平方差出来吧，能少几项能省不少时间啊

用户头像
郝一然
10月前
数学高联一试课，计数与概率第五讲组合恒等式第一题。
结果为n(n+1)(2n+1)(3n^2+3n-1)/30
用户头像
人畜无害的钝人
10月前
三个字

1718719958768.jpg

1条评论
用户头像
人畜无害的钝人
10月前

虾找的

用户头像
羌水
9月前

似乎这样IMG_20240725_113755_009.jpg

用户头像
阿尔伯特.爱因斯坦
9月前
Σis an answer
用户头像
，
9月前
我印象里是要与伯努利数有关，要用到二项式定理，你可以去b站搜这个up：泰勒猫爱丽丝，有一期视频就详细讲了伯努利对于这样类似的求和的推导
用户头像
黄智英（备战高考版）
8月前
如下图

IMG_20240726_130236_004.jpg

1条评论
用户头像
Beijing subway
8月前

🤑🤑🤑

用户头像
清梦里
8月前
！！！