- 1
知乎上有，但是我看的不是很明白……
我没太看懂他这个是怎么得到的，但我学了一下分离变量，能解出来一堆级数
可以试试用MATLAB
我太菜了，你的很多问题我都不会
佬别这么说，你已经帮助了我很多了
还有佬高考加油
诶•̀.̫•́✧？城佬哪天高考，可以找伊文斯开一个祈福帖我们论坛上得到过城佬帮助的宝都给城佬祈福加油叭～～(≧∇≦)b～～
(； ･`д･´)
@三等分的伊文斯@物理之城2024/6/7，还有13天
祈福帖我觉得没必要，我的每一篇帖子（除了题目互答）的评论区都可以祈福
电路自由度那个问题我去问了@一个听K-391的物竞牲（怎么把平板背回去了没来论坛，绝对又在卷……）
他说应该是把这个问题类比成了一个力学问题，把它看做了一个振动（具体表达意思可能有偏差，等他本人来看看）
感觉题很好，自己先做一下
（我也不一定算对，我很菜的；建议大佬们先独立完成，再检查我的有没有出错）
题0.2
(1)
$t_1'=\dfrac{\sqrt5l}{c}$
$x_B'=l+vt_1'=l+\dfrac{\sqrt5lv}{c}$
$t_1=t_1'\sqrt{1-v^2/c^2}=\dfrac{\sqrt5l}{c^2}\sqrt{c^2-v^2}$
(2)
$l_1=l\sqrt{1-v^2/c^2}$
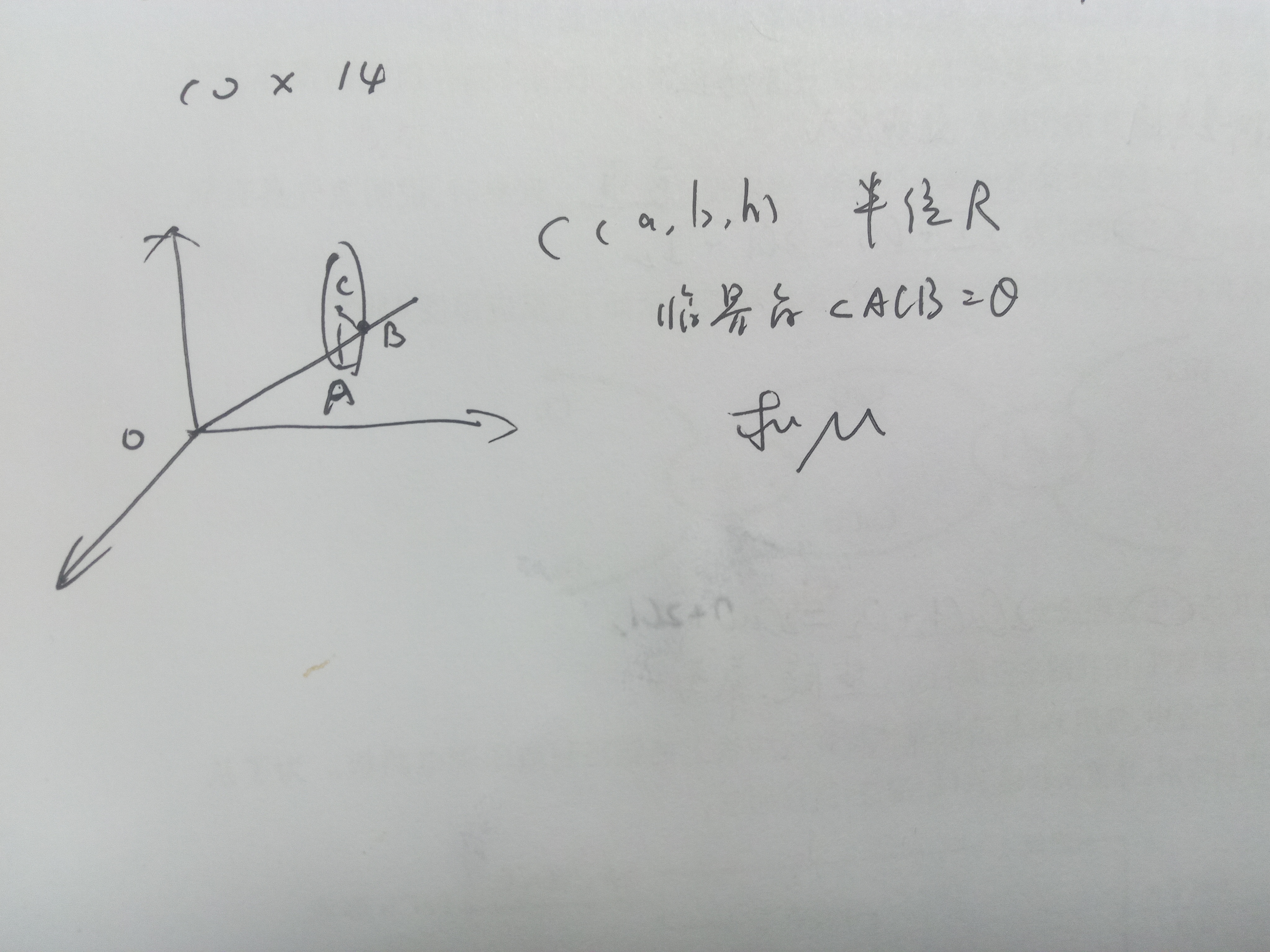
(3)
$t_2=\dfrac{2l}{c\sin\theta}$
$vt_2+l_1=ct_2\cos\theta$
$\Rightarrow 2v+\sqrt{c^2-v^2}\sin\theta=2c\cos\theta$
$\sin\theta=\dfrac{2\sqrt{c^2-v^2}}{\sqrt{5}c+v}$
$t_2=\dfrac{l(\sqrt{5}c+v)}{c\sqrt{c^2-v^2}}$
$x_B=vt_2+l_1=\dfrac{lv(\sqrt{5}c+v)+l(c^2-v^2)}{c\sqrt{c^2-v^2}}$
$t_2'=t_2\sqrt{1-v^2/c^2}=\dfrac{l(\sqrt{5}c+v)}{c^2}$
佬，你的我的还有答案的好像都不太一样
答案是怎么做的？我觉得相对论太难了
我的第一行订正，用的速度变换，下面是我的解法，用的位置变换
没看懂，我太菜了（看来相对论要重新学了）
你看看我的题0.1做得对不对
因为我太菜了，所以再做一下题0.1
(1)
$\mathrm{d}E_p=\dfrac{Gm\mathrm{d}m}{r}$
$m=\dfrac{r^3}{R^3}M$
$\mathrm{d}m=\dfrac{3r^2\mathrm{d}r}{R^3}M$
$\mathrm{d}E_p=\dfrac{3GM^2r^4\mathrm{d}r}{R^6}$
$E_p=\dfrac{3GM^2}{5R}$
(2)
$P=4\pi R^2\sigma T^4$
$t=\dfrac{E_p}{P}=\dfrac{3GM^2}{20\pi R^3\sigma T^4}$
(3)
$E_p=cMT$
$T=\dfrac{3GM}{5Rc}$
$E_p'=\dfrac{3GM^2r^5}{5R^6}=c\dfrac{r^3}{R^3}MT_C$
$r^2=\dfrac{5cR^3T_C}{3GM}$
$\dfrac{m}{M}=\dfrac{r^3}{R^3}=(\dfrac{5cRT_C}{3GM})^{\small\frac{3}{2}}$
是对的，佬太厉害了
顺便问一个问题，一个杆搭在一个环上，临界状态下摩擦力向哪
我一点都不厉害，只是题0.1比较简单而已
你这个问题能描述得具体一些吗？
