§1 Newton力学

§1.1 时空观

Newton力学中的时空观认为我们处在一个平直的3维Euclid空间$(x,y,z)$中，并且有时间$t$的推移，一般将质点的位置矢量定义为

$$\vec{r}=x(t)\hat{i}+y(t)\hat{j}+z(t)\hat{k}$$

对应的我们可以定义速度和加速度

$$\begin{aligned}\vec{v}&\equiv\frac{d\vec{r}}{dt}=\dot{\vec{r}}\\\vec{a}&\equiv\frac{d\vec{v}}{dt}=\ddot{\vec{r}}\end{aligned}$$

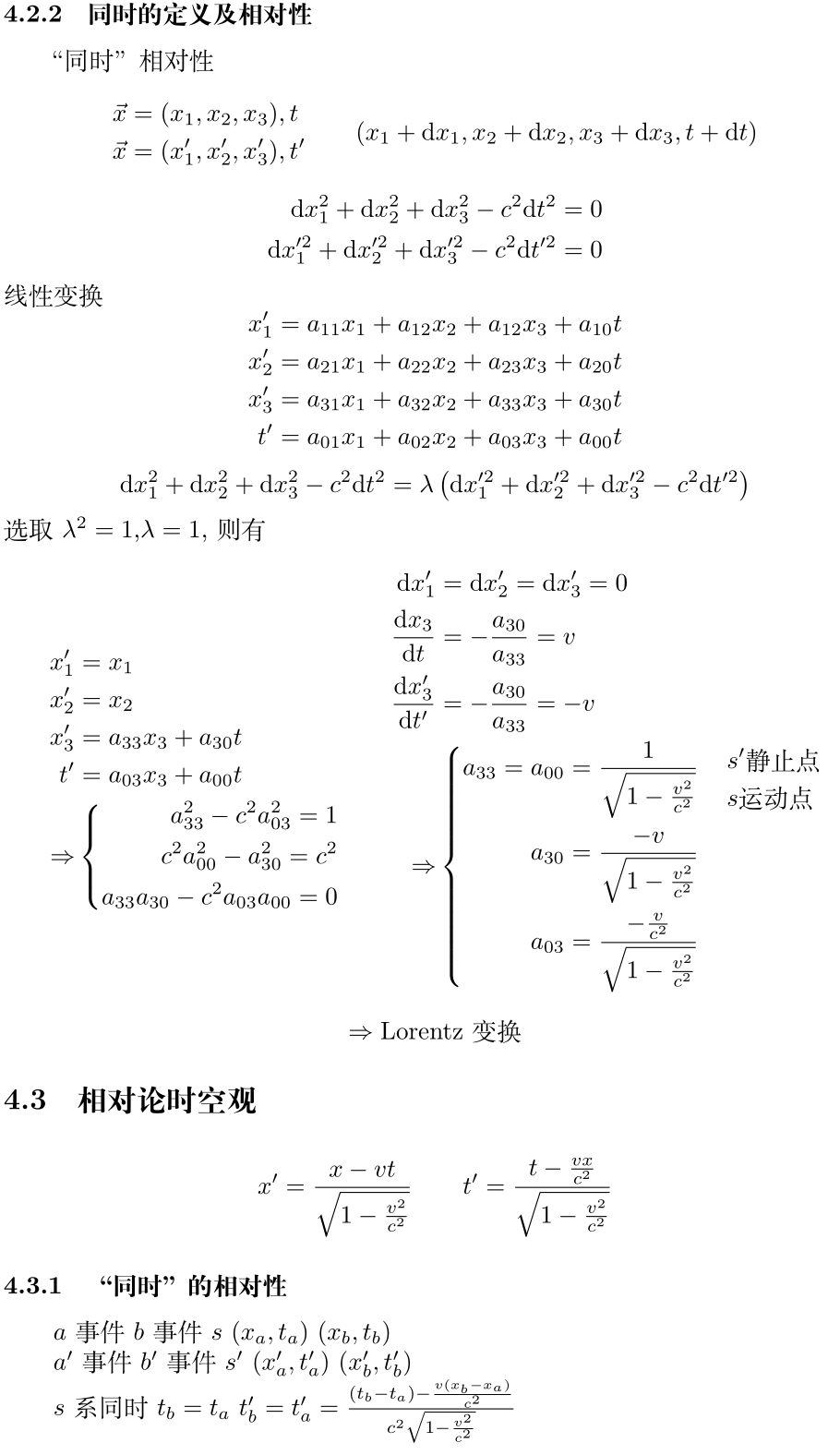
具体而言，Newton力学的时空观可以用Galileo变换描述，除了坐标之间的简单线性变换外，Galileo变换的主要特点：相对匀速运动的参考系之间所用时间认为完全相同。

§1.2 Newton运动定律

Newton第一定律 孤立质点保持静止或做匀速直线运动。

Newton第二定律 $\vec{F}$为质量为$m$的物体某时刻受到的合外力，$\vec{a}$为该物体该时刻的加速度，则有

$$\vec{F}=m\vec{a}$$

Newton第三定律 相互作用的两个质点之间的作用力和反作用力总是大小相等，方向相反，作用在同一条直线上。

问：若研究系统为孤立质点，在$\psi(\vec{r})=-G\frac{M}{r}$，标量场Newton第二定律中，合外力为零，则可根据公式自然地得到Newton第一定律，为什么还需要第一定律?

答：Newton第一定律定义了惯性，从而可以定义惯性系，而Newton运动定律的成立条件便是在惯性系下，因此Newton第一定律可以说是给出了第二定律的成立前提条件，不能省略。

§1.3 行星运动定律——Kepler定律

Kepler第一定律（椭圆定律）所有行星绕太阳的轨道都是椭圆，太阳在椭圆的一个焦点上。

Kepler第二定律（面积定律）行星和太阳的连线在相等的时间间隔内扫过的面积相等。

Kepler第三定律（调和定律）所有行星绕太阳一周的恒星时间$T_{i}$的平方与它们轨道半长轴$a_{i}$的立方成比例，即：$\frac{a_{1}^{3}}{T_{1}^{2}}=\frac{a_{2}^{3}}{T_{2}^{2}}$。

§1.4 经典引力场

若引力场$\psi(\vec{r})$，则

$$\vec{g}=-\nabla \psi(\vec{r})=-\frac{\partial \psi(\vec{r})}{\partial x}\hat{i}-\frac{\partial \psi(\vec{r})}{\partial y}\hat{j}-\frac{\partial \psi(\vec{r})}{\partial z}\hat{k}$$

$\psi(\vec{r})=-G\frac{M}{r}$，标量场

$$\nabla\cdot\vec{g}=\frac{\partial g_{x}}{\partial x}+\frac{\partial g_{y}}{\partial y}+\frac{\partial g_{z}}{\partial z}=-\nabla^{2}\psi(\vec{r})$$

Laplace算子

$$\Delta=\nabla^{2}=\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\frac{\partial^{2}}{\partial z^{2}}$$

注：$\nabla$—三维，$\square$—四维

$$\iiint\delta(\vec{r})\,\mathrm{d}^{3}\vec{r}=1\qquad \nabla^{2}\frac{1}{r}=-4\pi\delta(\vec{r})$$

$$\nabla^{2}\psi(\vec{r})=4\pi GM\delta(\vec{r})$$

$\rho(\vec{r})$

$$\begin{aligned}\vec{g}&=-\iiint\mathrm{d}^{3}\vec{r}G\frac{\rho(\vec{r})}{R^{2}}\frac{\vec{R}}{R}\\\psi(\vec{r})&=-\iiint\mathrm{d}^{3}\vec{r}G\frac{\rho(\vec{R})}{R}\end{aligned}$$

Possion方程

$$\nabla^{2}\psi=4\pi GM\delta(\vec{r})$$