物理

力学小专题

不完整(完结)

1. 牛顿第一定律：F=ma

2. 牛顿第二定律：F=dp/dt

3. 牛顿第三定律：F12 = -F21

4. 动能定理：K = 1/2 mv^2

5. 动量定理：I = FΔt

6. 机械能守恒定律：E = K + U

7. 万有引力定律：F = G(m1m2/r^2)

8. 转动惯量：I = Σmiri^2

9. 角加速度公式：α = Δω/Δt

10. 动量守恒定律：Σmi1vi1 = Σmi2vi2

11. 动能守恒定律：K1 + U1 = K2 + U2

12. 简谐振动的角频率：ω = √(k/m)

13. 滑块和斜面问题：F = ma, N = mgcosθ

14. 瓦特定律：P = W/t

15. 高度位能：U = mgh

16. 力矩定律：τ = r×F

17. 线性动量：p = mv

18. 转动力矩：τ = rFsinθ

19. 动能公式：K = 1/2Iω^2

20. 转动动量：L = Iω

21. 线性速度与角速度的关系：v = rω

22. 等效质量：1/Me = 1/m1 + 1/m2 + … + 1/mn

23. 包络曲线的速度：v = √(rg)

24. 弹簧振子的运动方程：mx'' + kx = 0

25. 斜面上滑动物体的加速度：a = gsinθ

26. 斜面上静摩擦力的最大值：f = μsN

27. 伯努利定理：P + 1/2ρv^2 + ρgh = 常数

28. 应变能量：U = 1/2kx^2

29. 斯托克斯定理：∮F·dr = ∬(∇×F)·dA

30. 阿基米德原理：F浸 = ρVg

在运动学中，我们经常使用直角坐标、自然坐标和极坐标进行描述。

下面是它们的微分表达：

1. 直角坐标系：如果一个物体在直角坐标系中以速度(vx,vy)移动，那么它在x轴和y轴方向的位移分别为dx= vx*dt和dy= vy*dt。

物体的速度可以通过vx=dx/dt和vy=dy/dt得到。

2. 自然坐标系：自然坐标系通常用来描述圆周运动或曲线运动。如果一个物体在自然坐标系中以速度(vr,θ)移动，那么它在径向和角向的位移分别为dr= vr*dt和dθ= θ*dt。

物体的速度可以通过vr=dr/dt和θ=dθ/dt得到。

3. 极坐标系：极坐标系常用于描述圆周运动。在极坐标系中，如果一个物体以速度(vr,r)移动，那么它在r方向和角度方向的位移分别为dr= vr*dt和dθ= r*dt。

物体的速度可以通过vr=dr/dt和r=dθ/dt得到。

速度加速度的两种通用解法在运动学中是非常重要的。一种解法是平动系解法，另一种是转动系解法。

1. 平动系解法（平移运动）：在平动系解法中，我们通常使用直角坐标系描述物体的运动。

假设一个物体在直角坐标系中以速度(vx,vy)移动，则其位置可以用x= x0 + vx*t和y= y0 + vy*t表示，其中(x0, y0)是初始位置，t是时间。

加速度的表达式可以用ax= d(vx)/dt和ay= d(vy)/dt得到。

2. 转动系解法（曲线运动）：在转动系解法中，我们通常使用极坐标系描述物体的运动。

假设一个物体在极坐标系中以速度(vr,θ)移动，则其位置可以用r= r0 + ∫(vr*dt)和θ= θ0 + ∫(dθ)表示，其中(r0, θ0)是初始位置，t是时间。

加速度的表达式可以用ar= d(vr)/dt和aθ= r*(dθ)/dt + 2*vr表示。

对于包络线的一般解法，其实是一种复杂的问题，通常解法包括用微积分和微分方程来描述和求解。

对于一般的包络线问题，我们需要利用变量之间的关系和约束条件来建立方程，并求解得到包络线的方程。

以机械学为例，如果我们需要找到一个系统中运动物体的包络线，可以先根据系统中各个物体的速度和加速度来建立关系式，然后利用微积分求解约束条件下各个物体轨迹的交点来得到包络线的方程。

总之，包络线问题的一般解法通常需要通过建立约束条件和使用微积分和微分方程来描述和求解。

具体问题的解法可能需要具体分析和使用不同的数学工具。

微分方程在运动学中有着重要的应用，其中一个常见的例题就是关于质点的运动。

假设一个质点在某一时刻的速度为v，根据牛顿第二定律（F=ma），可以得出质点的加速度a。

如果假设质点受到某个力的作用，那么可以通过微分方程来描述质点的运动。

微分方程的一般形式可以写成F=ma，其中F是力，m是质量，a是加速度。

如果知道力的表达式，就可以通过微分方程求解质点的运动轨迹。在解析上，可以通过微分方程求解质点的轨迹方程，从而得到质点在不同时刻的位置和速度。

这有助于研究质点的运动规律，对于物体的运动学关联问题有着重要的意义。

在拓展上，微分方程还可以用于描述其他物体的运动，如刚体、弹性体等。

通过微分方程的建模分析，可以得到这些物体的运动规律，为运动学研究提供更多的手段。

空间力矩问题是运动学中的一个重要问题，可以通过微分方程描述物体在空间中的力矩和角加速度，从而得到物体的角速度和角位移。

通过微分方程分析，可以研究物体在空间中的旋转运动。

另外，微分方程也可以应用于连续体的形状分布深度分析。

例如，在弹性体力学中，可以通过微分方程描述物体受力后的形状变化和应力分布，从而分析物体的形变和变形情况。这对于材料工程、土木工程等领域有着重要的意义。

在连续体力学中，微分方程也可以用来描述流体力学问题。通过微分方程，可以表达流体的运动和流速分布，从而研究流体的动力学性质，包括涡旋、湍流等现象。

这对于航空航天、海洋工程、水利工程等领域有着重要的应用价值。

总之，微分方程在运动学关联、空间力矩问题以及连续体形状分布深度分析方面都有着丰富的应用。

通过微分方程建模分析，可以研究各种物体的运动规律和形变情况，为工程技术和科学研究提供了重要的工具和方法。

科里奥利力是指在旋转参考系下，物体所具有的可观测为偏转的力。

在三维空间中，科里奥利力可以通过动力学方程和向导来描述。

一个典型的动力学例题是考虑一个质点相对于一个以角速度ω沿z轴旋转的参考系的运动。

在这种情况下，质点会在x和y方向上受到科里奥利力的作用。

可以使用动力学方程

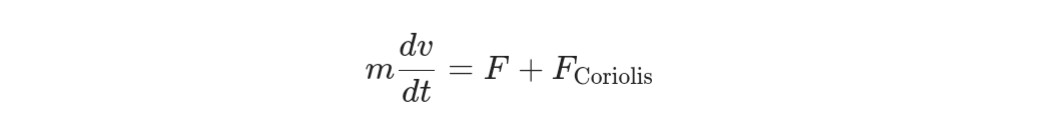
来描述这种情况下质点的运动，其中F是外部施加的力，F_{ ext{Coriolis}}是科里奥利力。

解析上，可以通过求解微分方程来分析质点的运动轨迹。可以得到质点在旋转参考系下的运动规律，包括速度、加速度和位移等方面的信息。在拓展上，三维空间中的科里奥利力可以进一步应用于天体力学、航空航天等领域。

在天体力学中，如行星、卫星等天体的运动也受到科里奥利力的影响，通过动力学方程可以对其运动进行分析和预测。

冲量计算的化简技巧：

1. 利用矢量分解：将物体的冲量矢量进行分解，然后分别计算各个方向上的冲量，最后将各个方向上的冲量矢量相加得到总的冲量。

2. 利用动量守恒定律：当系统内部没有外力做功时，系统的总动量守恒，可以利用这一定律简化冲量的计算。

3. 利用简单形状的质点模型：在一些简单的情况下，可以将物体看作质点来计算冲量，从而简化计算过程。

冲击力和冲击摩擦：冲击力是在瞬间内作用在物体上的力，通常导致物体的速度发生突变，而冲击摩擦是指在两个物体在瞬间内接触并发生相互作用时，产生的摩擦力。

冲击力和冲击摩擦都属于短暂且瞬间的作用力，需要根据具体情况对其进行分析和计算。

柯尼希定理：柯尼希定理是关于刚体转动的定理，其表述为：

在刚体作定轴转动时，刚体上每一点的线速度的平方与角速度的乘积的平方可表示为常数。

即 v^2 = ω^2 * r^2。其中，v代表刚体上某一点的线速度，ω代表刚体的角速度，r代表刚体上该点距离。

质心运动：质心是一个物体或系统中所有质点的平均位置。

质心运动是指系统质心位置随时间的变化。质心运动可以通过系统质量与各质点位置的加权平均来描述。

它是一个重要的概念，对于研究系统整体运动具有很大的意义。

相对质心运动：当一个物体或系统中的多个质点之间有相对运动时，我们可以使用相对质心运动来描述这些质点之间的运动关系。相对质心运动是以质心为参照点来描述各个质点的相对运动状态。

大质量物体能量：大质量物体的能量可以通过其质量和速度来计算。根据相对论的能量-动量关系E^2 = (pc)^2 + (m0c^2)^2，其中E为能量，p为动量，c为光速，m0为静止质量。

对于大质量物体，需要考虑相对论效应，而非相对论效应下，其能量可以简化为动能和静能的总和。

拉格朗日方程深度分析：拉格朗日方程是经典力学中描述系统运动的数学工具，它将系统的动力学问题转化为最小作用量原理的变分问题。

拉格朗日方程可以用来描述复杂的运动，涉及不定形的约束。

例如，一个受到限制运动的质点，同时考虑它的势能和动能。这样的系统可以由拉格朗日方程来描述。

拉格朗日方程的一般形式是：L = T - V其中，L代表拉格朗日量，T代表动能，V代表势能。

通过对拉格朗日量的偏微分和对时间的导数来得到运动方程。这些运动方程描述了系统在所有可能的运动路径上所满足的条件。

拉格朗日方程在描述系统的运动时具有许多优点，如不变性、适用于多种坐标系、在处理约束系统时的方便性等。

因此，它是研究经典力学问题的重要工具。对于更加深入的讨论，还可以涉及到广义坐标、虚位移、哈密顿原理等。拉格朗日方程的深度分析需要对数学物理知识有较为扎实的理解。

广义坐标：在描述多自由度系统的运动时，广义坐标是一种在坐标空间中描述系统的方法。

它是描述系统位形的一组坐标，能够唯一确定系统的状态。与直角坐标系不同，广义坐标不必是直角坐标系的坐标，它可以是曲线坐标、极坐标、广义正交曲线坐标等。

虚位移：虚位移是研究力学问题时经常使用的一种概念。当物体受到约束时，它的实际运动可能受到一定的限制。虚位移是指对系统的位移做微小变化，而其他条件不变。

通过对虚位移的分析，可以得到系统所满足的运动方程，这为研究问题提供了方便。

哈密顿原理：哈密顿原理是古典力学中具有重要意义的原理之一。

它也被称为变分原理。

该原理的表述是：对于一个运动的系统，在所有可能的轨迹中，真正的轨迹使作用量取一个极值。

这个作用量是拉格朗日量在一段时间内的积分。哈密顿原理提供了一种独特的观点来描述力学系统的运动规律，它与拉格朗日方程具有密切的联系。

通过哈密顿原理，我们可以得到哈密顿-雅可比原理，并由此导出哈密顿力学方程。

刚体的定轴转动和平面平行运动是刚体运动学中的两种重要运动形式。

定轴转动是指刚体绕固定轴进行旋转运动。

在定轴转动中，刚体上各个点的运动状态可以用角位移、角速度和角加速度来描述。角位移描述了刚体绕轴的旋转角度，角速度描述了刚体围绕轴的旋转速度，角加速度描述了刚体绕轴的旋转加速度。

平面平行运动是指刚体在平面内进行平移运动，且其运动轨迹保持平行。

在平面平行运动中，刚体上各个点的运动状态可以用位移、速度和加速度来描述。

位移描述了刚体从一个位置到另一个位置的距离和方向，速度描述了刚体在单位时间内移动的距离和方向，加速度描述了刚体在单位时间内速度的变化率。

刚体的进动是指刚体在固定轴上进行定轴转动的同时，整体发生平移运动的现象。

在进动运动中，刚体上各个点的运动状态可以用角位移、角速度、角加速度和位移、速度、加速度来描述，并且这些描述量的组合要满足相应的物理关系。

转动惯量张量是描述刚体转动惯量的一种数学工具。对于一个刚体在空间中的旋转运动，其转动惯量可以使用转动惯量张量来描述。

转动惯量张量是一个描述物体对于不同转轴的转动惯量的三阶张量，通常使用一个3x3的矩阵来表示。

根据刚体的形状和质量分布，转动惯量张量可以被计算出来，它可以反映刚体在不同轴上的旋转运动惯性大小和方向的分布情况。转动惯量张量的主轴和主转动惯量是在特定形势下，对应于转动惯量张量的特征向量和特征值。

主轴是转动惯量张量的特征向量所代表的轴线方向，而主转动惯量是对应于主轴的特征值，它代表了沿主轴的旋转惯量大小。

对于刚体的运动，特别是围绕固定轴的旋转运动和转动惯量的分析，转动惯量张量的概念和计算是非常重要的。

它帮助理解刚体在空间中的旋转运动特性，对于理解刚体的稳定性、动力学和工程应用都具有重要意义。

相对运动在天体力学中是一个非常重要的概念，因为它允许我们研究天体之间的相互作用。

在天文学中，由于天体之间的质量和距离差异巨大，并且有多个天体相互影响的情况，所以相对运动的考虑十分重要。一般算法用于解决天体问题，包括了牛顿引力定律和牛顿运动定律。

牛顿引力定律描述了两个物体之间的引力大小与它们的质量和之间的距离平方成正比，而与它们的运动状态无关；牛顿运动定律描述了物体的运动状态，以及受到的作用力和加速度之间的关系。

这两个定律结合起来允许我们建立微分方程来描述天体在引力作用下的运动状态。

在天体力学中，进动是指天体的自旋轴线在空间中缓慢画圆或者椭圆的运动。

这种运动可以是由各种引力扰动和非圆球形的天体形状所引起的。

这种现象在行星、卫星和其他宇宙体的运动中都有所发现。非平方反比有心力下的天体运动是指在引力为非平方反比的力场中天体的运动。

非平方反比有心力指的是引力与距离的平方成反比，例如万有引力定律描述了这样一种有心力。在这种力场下，天体的运动不再是简单的椭圆、圆形轨道，而是具有独特的轨道形态，这对于天体力学的研究提出了挑战，但也给我们带来了更加丰富和复杂的天体运动形式。

LRL矢量是天体力学中的一个重要概念，它描述了天体的角动量、径向动量和能量之间的关系。LRL矢量可以用来描述天体运动的几何特征和动力学特性。

通过对LRL矢量的计算和分析，可以帮助我们理解天体在引力场中的运动规律，并且在天体轨道设计、航天器轨道控制等方面有着重要的应用。

天体力学是一个复杂而重要的领域，研究天体之间的相互作用和运动规律，它涉及到物理学、数学和工程学等多个学科领域。

对于天体力学的研究和应用有着广泛的意义，不仅可以帮助我们更加深入地理解宇宙的运行规律，还能够为人类的太空探测和开发提供重要的科学依据。

简谐振动是指一个物体在外力作用下沿着某一方向做周期性的来回运动，它的加速度与位移成正比且方向相反。简谐振动可由以下方程描述：

m*x''(t) + k*x(t) = F(t)其中，m是物体的质量，x(t)是物体的位移，k是弹簧的劲度系数，F(t)是外力。

在微扰下的近似简谐振动中，我们可以假设外力F(t)相对于弹簧的劲度系数k比较小，这样可以用微扰理论来近似描述简谐振动，从而得到一个新的方程。

通过对新的方程进行相位计算，可以得到微扰下的近似简谐振动的运动规律。

圆的应用可以帮助我们理解简谐振动的运动规律，因为圆的正弦函数和余弦函数可以描述简谐振动的位移和速度，从而直观地理解振动的周期、幅度和相位等重要参数。

而对于刚体摆动的周期，可以通过能量泰勒展开来求得。

将刚体摆动的能量表达式进行泰勒展开，然后通过对其周期进行求导，可以得到刚体摆动的周期。

在固体中，应力指的是单位面积上的力量。当外部力施加在固体表面上时，会产生内部应力。这些应力可以由几种类型的力引起，包括张力、剪切力和压力。

应力可以是正的（拉伸）也可以是负的（压缩）。材料的弹性、塑性和断裂行为取决于应力的大小、方向和作用时间。

应力波是指在固体中传播的应力异常，它是由固体内部的应力扰动引起的。应力波可由外部冲击、震动或者其他应力扰动引起。应力波传播的速度取决于材料的弹性性质，例如密度、弹性模量等。

当应力波到达固体边界时，它可能会反射、折射或透射，根据固体的几何形状、密度和弹性性质等因素。

应力波的传播和反射行为对于地震、声波、冲击波以及材料断裂等现象都具有重要的意义。

对应力波的研究有助于理解材料的力学性质以及在工程和地质领域中的应用，比如地震勘察、深海探测和结构损伤检测等。

线性微分方程在力学中有着广泛的应用，比如描述运动、振动、材料力学和流体力学等现象。以下是一个例题：

考虑一个简谐振动系统，其运动可以由线性微分方程描述：

m*x''(t) + k*x(t) = F(t)其中m是系统的质量，x(t)是系统的位移，k是系统的弹簧常数，F(t)是外部作用力。我们可以使用线性微分方程来分析系统的振动特性，并求解系统的位移。

解析：对于上述方程，我们可以求解出系统的位移x(t)随时间的变化规律。

通过分析解的属性，我们可以获得关于系统振动频率、振幅和相位等重要信息。

拓展：线性微分方程还可以用于描述复杂的力学问题，比如弹性体的变形、非均匀材料的应力分布、流体的运动等。

通过数学建模和求解线性微分方程，可以深入理解各种物理现象的力学特性。

总结：线性微分方程在力学中扮演着重要角色，它们为我们提供了描述系统运动和振动的数学工具。

通过解析和拓展，我们可以更好地理解和预测力学现象。

二次线性递推数列在力学中有着广泛的应用，特别在振动现象的研究中。在力学中，通过建立适当的数学模型，可以将振动问题转化为二次线性递推数列的问题。以下是一个例子：

考虑一个质点在弹簧-质点系统中的振动。通过牛顿第二定律和胡克定律，可以得到该系统的运动方程：m*x''(t) + k*x(t) = 0其中m是质点的质量，x(t)是质点的位移，k是弹簧的劲度系数。

这个方程可以被转化为二次线性递推数列形式。通过求解这个数列，我们可以分析质点的振动特性，比如振动的频率、振幅和相位等。

另一个力学中的例子是简正膜，简正膜是指在分子结构中，在平衡位置上小范围的物理位移，而将分子的位移看作关于时间的特定函数。

简正膜的研究也可以转化为二次线性递推数列的问题。

通过求解这些数列，可以研究材料的分子振动特性，如声子色散关系、声子态密度等。

总之，二次线性递推数列在力学中有着重要的应用，特别在振动和分子振动等领域中发挥着重要的作用。

三体力学是研究三个物体之间相互作用的力学问题，通常涉及到引力、碰撞、运动轨迹等方面的分析。在三体力学中，最常见的问题是三个物体之间的引力相互作用。

根据万有引力定律，每个物体之间都会相互施加引力，其大小与质量和距离的平方成反比。因此，在三体问题中，需要分析每个物体在其他两个物体的引力作用下的加速度和轨迹。

三体问题的解决通常需要数值模拟或者近似算法，因为其数学公式很难直接求解。其中比较著名的是“拉格朗日点”和“霍曼传送”方法，它们分别通过合适的坐标系转换和轨道选择来简化三体问题的分析。

除了引力相互作用外，三体问题还涉及到碰撞和动量守恒等物理原理。在三体碰撞中，需要分析每个物体的动量变化和能量转化，以确定碰撞后的运动状态。这也需要应用动量守恒和能量守恒的定律。

总的来说，三体力学是一个复杂的物理问题，需要综合运用牛顿力学、引力定律、动量守恒等物理原理进行详细分析。通过数值模拟和近似算法。

附：1. 折射定律：$n_1 sin( heta_1) = n_2 sin( heta_2)$

2. 薄透镜成像公式：$rac{1}{f} = rac{1}{d_o} + rac{1}{d_i}$

3. 透镜公式：$rac{1}{f} = (n-1) (rac{1}{R_1} - rac{1}{R_2})$

4. 光的波长与频率的关系：$v = f lambda$

5. 镜面反射定律：$ heta_i = heta_r$

6. 球面反射成像公式：$rac{1}{f} = rac{1}{d_o} + rac{1}{d_i}$

7. 折射率与入射角的关系：$n = rac{sin( heta_i)}{sin( heta_t)}$

8. 牛顿环半径公式：$r^2 = rac{(m + rac{1}{2}) lambda R}{n}$