物理

电磁学专题

不完整(完结)

1. 库伦定律：F = k|q1q2|/r^2

2. 电场强度与电场受力关系：F = Eq

3. 高斯定理：Φ = ∮E·dA = Q/ε0

4. 电场能量密度：u = 1/2ε0E^2

5. 电势能：U = qΔV

6. 电荷点产生的电势：V = kq/r

7. 电容器的电容公式：C = Q/ΔV

8. 电流强度与电荷的关系：I = ΔQ/Δt

9. 欧姆定律：V = IR

10. 电阻的电功率公式：P = I^2R = V^2/R

11. 磁感应强度与洛伦兹力的关系：F = qvBsinθ

12. 安培环路定理：∮B·dl = μ0I

13. 安培力定律：F = μ0I1I2l/(2πr)

14. 磁场能量密度：u = B^2/2μ0

15. 感生电动势：ε = -ΔΦ/Δt

16. 洛仑兹力：F = q(E + v×B)

17. 磁通量：Φ = ∮B·dA

在真空中，电荷会以自由态的形式存在，而不会受到外界物质的影响。

这就意味着电荷可以在真空中移动，并且会产生电场。

电场的分布会随着电荷的移动而改变，但在真空中，电场的性质与分布是由电荷的位置和性质所决定的。在真空中，电场的分布会随着电荷分布的变化而变化。

电场是沿着空间的力的表示，它会围绕电荷分布形成。如果有正电荷，电场线将从正电荷流向负电荷。

如果有负电荷，电场线将从负电荷流向正电荷。电场的强度与电荷的大小有关，与距离的平方成反比。

在真空中，电势是描述空间中某一点上电场势能的物理量。电势是标量，它是在电场中某一点上，单位正电荷所具有的势能。

电势的分布与电荷分布及电场强度有关，通常电势随着距离的增加而减小。

高斯定理和斯托克斯定理是物理学和工程学中电场、磁场和流体力学等领域的两个重要的矢量场定理。

1. 高斯定理（也称为高斯散度定理）:高斯定理是描述矢量场散度的定理。

它说明了一个矢量场穿过一个闭合曲面的总量，与该曲面所包围的体积内该矢量场的源的总量之间的关系。具体来说，如果V表示一个封闭的曲面，S表示该曲面的有限三角剖分以及法向量，F表示在整个V内可微的矢量场，

则高斯定理的数学表示为：∬_V  (F·n)dS = ∭_V  ∇·FdV这里∬_V表示曲面积分，∭_V表示体积积分，(F·n)表示矢量场F与曲面法向量n的点积，∇·F表示矢量场F的散度。

简而言之，高斯定理说明了通过一个闭合曲面的矢量场的通量与该曲面内部的源强度之间的关系。

2. 斯托克斯定理:斯托克斯定理描述了矢量场环路积分与通过某个有限曲面的曲面积分之间的关系。具体来说，对于一个有向曲面S和边界C，还有一可微矢量场F，

斯托克斯定理的数学表示为：∮_C  (F·dr) = ∬_S  (curl F) ·dS在这里，∮_C 表示对曲线 C 的环路积分，F·dr 表示矢量场 F 和微位移向量 dr 的点积，∬_S 表示对曲面 S 的曲面积分，curl F 表示矢量场 F 的旋度，dS 表示曲面 S 上的面积元素。

斯托克斯定理说明，通过沿着有向曲线 C 的环路积分与通过曲面 S 的曲面积分之间存在一个关系。

这个定理常用于电磁场的计算以及流体力学等领域中研究流体的旋转和环流等问题。

总体来说，高斯定理和斯托克斯定理都是通过研究矢量场在不同维度上的积分关系来描述场的性质和分布的重要定理，它们在物理学和工程学中有着广泛的应用。

流速场是描述流体运动状态的重要物理量，它是流体中流动粒子在单位时间内通过某一截面的数量。

它可以用矢量场表示，即在空间中的每一点都有一个速度矢量与之对应。

通量是指单位时间内通过给定表面的流体或其他物理量的总量，可以用来描述流体或其他物理量的通过某一表面的流动情况，通量的大小与表面的大小和方向以及流速场的值有关。环量是指围绕某一闭合路径的流场的总量，它可以用来描述流体沿着闭合路径运动时所带来的影响。

电偶极子是指由两个等量异号的电荷构成的一个系统，它们之间的距离相对于整个系统来说很小，从远处观察时，它们的电场与单个电荷产生的电场形式相似，但是方向相反。

电四极子是指由四个电荷构成的一个系统，它们之间的距离比电偶极子大，从远处观察时，它们产生的电场则包含了偶极矩和四极矩的效应，其电场的形式比电偶极子更加复杂。

总的来说，流速场、通量和环量是描述流体运动和对流量的重要物理量，而电偶极子和电四极子则是描述电荷分布产生产生的复杂电场的重要概念。通量与环量的概念在电磁学中也有类似的应用，用于描述电场和磁场的传播和影响。

电偶极子和电四极子则是用来描述电荷分布的复杂性，电偶极子描述了两个近距离的电荷间的相互作用，而电四极子则描述了四个电荷相互作用的情况。

它们在物理学和工程学中具有重要的应用，例如在分子结构、电子学和电场感应等方面都有重要的作用。

总的来说，这些概念在描述流体力学和电磁学中有着重要的应用，在科学研究和工程技术领域中发挥着重要的作用。

金属中的静电屏蔽是指金属对静电场的屏蔽效应。

当金属表面受到外部电场作用时，金属内部电荷会重新分布，在金属表面会产生一个与外部电场方向相反的电场，从而减弱外部电场的影响。这种现象使金属成为了常用的静电屏蔽材料，被广泛应用于电子设备和电磁脉冲防护等领域。

唯一性定理分析：在静电学中，唯一性定理指出了在给定边界条件下某一区域内电场的分布是唯一确定的。

这一定理的应用可以帮助我们分析和解决各种与静电场分布相关的问题。例如，假设有一个金属球，外部有一个电荷q，我们可以利用唯一性定理来得出金属球内的电场分布。

由于金属是导体，外部电场会引起金属球表面的电荷分布，而根据唯一性定理，可以得知金属球内的电场应符合这一电荷分布所引起的电场。因此，我们可以利用唯一性定理分析金属球内的电场分布。

解析：对于金属中的静电屏蔽现象，可以从Maxwell方程组出发，利用高斯定律和静电学的基本知识来分析和描述金属内外电场的分布变化。

金属中的唯一性二三四维定理是固体物理学中的一个重要定理，它描述了金属在不同维度下的电子结构和性质。下面我们针对这一定理进行分析、提供例题与解析、拓展讨论并总结。

1. 分析

唯一性定理表明了金属在不同维度下的电子态密度以及费米面的性质。

在一维（线性）情况下，费米面是个点；

在二维（表面）情况下，费米面是个线；

而在三维（体积）情况下，费米面是个面。

这意味着金属的电子结构随着维度的增加而变得更加复杂。

而四维定理则是对应高维空间中金属性质的理论研究，通常与超导体等现象相关。

2. 例题与解析例题：对比一维、二维和三维金属中的费米面特征。

解析：在一维金属中，费米面是个点；在二维金属中，费米面是个封闭轮廓（线）；在三维金属中，费米面是个闭合表面。

3. 拓展唯一性定理的拓展可以涉及到更高维度的金属性质研究，以及在实验条件下对这些性质的观测。

另外，这一定理也可以与其他理论和实验结果相结合，来探讨金属性能与结构的关系。

4. 总结金属中的唯一性二三四维定理为我们提供了对金属电子结构在不同维度下的理论基础。

这一理论对于解释金属的电子性质和导电性提供了重要的指导，也为探索新型材料及其性质提供了理论基础。

在科学研究和工程应用中，唯一性定理的理论和实验研究成果也为我们提供了对金属材料行为和性质的深入理解。

5. 拓展讨论唯一性定理的拓展可以涉及到更高维度的金属性质研究，甚至是对金属在超高维度环境下的性质进行探索。

此外，也可以将唯一性定理应用到其他领域，例如金属的磁性、热性质以及与其他材料的界面相互作用等方面的研究中。

在实验方面，也可以探索利用新型技术手段或实验条件，对唯一性定理的预言进行验证。

总而言之，金属中的唯一性二三四维定理是固体物理学中的重要定理，它是对金属电子结构的深入理解和研究，为材料科学和工程提供了理论基础，并可能带来新型金属材料的设计和应用。

电容深度是指金属中电场衰减的深度，也可以理解为电场从金属表面向内部衰减至1/e（约0.37倍）的深度。金属中的电容深度对金属与电场的相互作用以及金属的电性能具有重要影响。

1. 电场作用金属中的电场会引发自由电子的移动，从而引起电流。电场在金属中的传播受到金属自由电子浓度和移动度的影响。电容深度较大的金属意味着电场能够影响较深的区域，而电容深度较小的金属则意味着电场在金属中的衰减较快。

2. 电容深度的影响电容深度的大小影响了金属的电磁波吸收能力、阻抗及材料的电导率等电性能。通常来说，电容深度 相对于金属中电磁波的波长具有显著影响。在光学和电磁学领域，电容深度也被用来描述金属的光学性质以及金属与外界电磁场的相互作用。

3. 计算方法电容深度与金属性质相关，

通常使用电容深度公式进行计算：

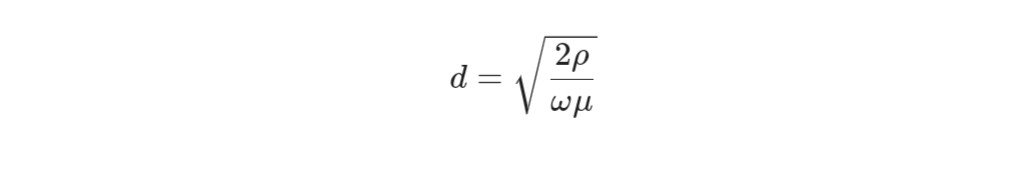
垂直边界电介质问题通常用于描述两个不同电介质（例如真空和介质）之间存在的电场的变化。这个问题可以用来研究介质的极化现象。下面我们将分别讨论二维、三维和四维球的极化和磁化问题。

1. 二维球的极化和磁化假设我们有一个二维球形电介质，球心位于原点。球的极化可能会导致球内部和外部的电场分布不同。在这种情况下，可以使用高斯定律和边界条件来解决这个问题。通过应用边界条件，我们可以计算出极化表面电荷和极化体积电荷。然后，我们可以求解出极化电场，并且考虑到介质中的磁化电流，应用安培环路定律计算出总电场。

2. 三维球的极化和磁化对于三维球形电介质，我们可以使用静电学和静磁学的理论来研究极化和磁化。同样，我们可以使用高斯定律和安培环路定律来分析内部和外部的电场和磁场。在求解极化和磁化问题时，还需要考虑材料的导磁性，以获得更加准确的电场和磁场分布。

3. 四维球的极化和磁化四维空间中的电介质和磁介质现象也可以用类似的方法进行分析。由于四维空间的复杂性，我们可能需要使用更加抽象的数学工具和理论框架（比如黎曼几何或爱因斯坦场方程）来描述四维球的极化和磁化现象。

总结：垂直边界电介质问题是一个重要的电磁学问题，可以通过边界条件求解出两个不同介质之间的电场和电荷分布。对于二维、三维和四维球的极化和磁化问题，都可以采用静电学和静磁学的方法进行求解，通过高斯定律、安培环路定律以及边界条件来获得电场和磁场的分布。在实际问题中，通常需要考虑介质的导电性、磁导率、极化率和磁化率等特性参数来更准确地描述电介质和磁介质的行为。拓展：进一步拓展可以涉及到对非球形、非均匀介质的极化和磁化问题的研究，同时还可以对时间变化下的极化和磁化现象进行分析，从而引入电磁感应和电磁波等现象。

总之，垂直边界电介质问题以及二维、三维和四维球的极化和磁化问题是电磁学中重要而有趣的研究领域，通过求解这些问题，我们可以更深入地了解电介质和磁介质在静电场和静磁场中的行为，从而为理论研究和应用开发提供基础。

介质中的电磁波在传播和相互作用方面有许多重要作用，下面将对介质中电磁波的作用和辐射本领进行解析：

1. 传播：介质中的电磁波可以传播到介质中，通过介质中原子和分子的振荡产生介质中的电磁波传播。这种传播往往受介质的电磁特性（比如电介质常数和磁介质导磁率）、介质中原子和分子的相互作用以及介质结构的影响。

2. 折射和透射：电磁波在介质中传播时，如果介质的折射率不同于真空或其他介质，则会发生折射。在介质与其他介质之间存在界面时，电磁波也会发生透射现象。

3. 吸收和衰减：介质中的电磁波会因电介质和磁介质的特性而被吸收和衰减。这种吸收和衰减导致电磁波在介质中的传播衰减和衍射。

4. 极化：介质中的电磁波通常会导致介质极化，其中分子和原子在电场中振动，产生局部电偶极子。这种极化行为是介质响应电场的结果，可以改变电磁波的传播特性。

5. 色散：介质中的电磁波频率通常会因介质的折射率和吸收特性而发生变化。这种现象称为色散。

微观欧姆定律是描述导体内部电荷载流子受外电场力作用的规律，即电流与电场强度之间的关系。导电体系的类比可以用水流和水管系统来解释，其中水流类比电流，水管系统类比导体。

根据微观欧姆定律，电场强度（E）与电流密度（J）之间的关系可以用以下公式表示：J = σE其中，J为电流密度，表示单位面积内通过的电流量；E为电场强度；σ为导体的电导率，表示单位长度内导体的电导能力。利用类比，我们可以把水流和水管系统的类比应用到导体电路中。

在水管系统中，水流速度可以类比电场强度，水管的直径可以类比导体的电导率，通过水管单位面积内的水流量可以类比电流密度。

根据类比，我们可以得出类比的微观欧姆定律：水流密度 = 水的电导率 × 水流速度解决导电体系问题时，可以利用微观欧姆定律来计算导体内部的电流密度和电场强度之间的关系，进而分析和设计电路系统。

同时，可以借助水流和水管系统的类比来帮助理解和解决导体系统中的导电问题。

当处理导电体系的问题时，我们可以利用微观欧姆定律和类比来解决各种与导体的电导能力和电流传输相关的挑战。例如，在电路设计中，我们可能需要确定导体的尺寸和材料，以使电流能够以所需的方式流动。通过微观欧姆定律和类比，我们可以计算出在给定电场强度下的预期电流密度，从而选择合适的导体材料和尺寸。

另外，当设计涉及到导电体系的传感器或其他电子器件时，我们需要考虑导体的电导率对电路性能的影响。通过微观欧姆定律和类比，我们可以理解和预测导体材料的电导率如何影响电路的响应和性能。

综上所述，微观欧姆定律提供了理解导电体系中电流与电场强度之间关系的基本规律，而类比可以帮助我们更直观地理解和解决实际问题。结合这两种方法，我们能够更好地设计和分析导体系统，以满足特定的电路需求和性能要求。

基尔霍夫定律是电路理论中较为核心的定律之一，用于描述电流在电路中的分配和流动。这个定律包括两个部分，即基尔霍夫电流定律（KCL）和基尔霍夫电压定律（KVL）。

1. 基尔霍夫电流定律（KCL）：指出在任何一个电路节点处，流入该节点的电流等于流出该节点的电流的总和。这可以表示为∑I_in = ∑I_out，其中∑表示对所有进出电流进行求和。

2. 基尔霍夫电压定律（KVL）：描述一个闭合电路中，沿着任何闭合路径（包括支路和回路）的电压之和等于零。这可以表示为∑V_loop = 0，其中∑V_loop表示对所有路径上的电压进行求和。星型（Y）与三角形（Δ）电路变换是在电路分析中经常用到的技术。在星型到三角形的变换中，三个电阻分别代表Δ型电阻的三条边，而在三角形到星型的变换中，三个电阻分别代表星型电阻的三条边。这些变换可以帮助简化复杂电路的分析。

对于带电粒子在静磁场中的轨迹，可以使用洛伦兹力来描述。当带电粒子在静磁场中运动时，其轨迹可以通过洛伦兹力来描述。洛伦兹力是指在磁场中运动的带电粒子所受到的力，其大小与电荷、速度以及磁场强度的方向都有关。

洛伦兹力可以用以下公式表示：F = q(v x B)其中，F表示洛伦兹力，q为带电粒子的电荷量，v为带电粒子的速度，B为所受的磁场强度，x表示矢量叉乘。这个公式表明洛伦兹力的大小与电荷的量、速度以及磁场的方向都有关。

带电粒子在磁场中的轨迹可以通过解洛伦兹力的微分方程来获得。粒子受到的洛伦兹力会使其在磁场中沿着特定的路径运动，这通常是曲线或螺旋线。对于特定的磁场形式和带电粒子的起始条件，可以使用数值计算或微分方程求解来确定带电粒子在静磁场中的轨迹。

这种分析对于理解粒子在磁场中的行为以及在磁场中的粒子束流以及等离子体物理等领域有重要意义。

1. 正则动量守恒：根据牛顿第三定律，系统内部作用力相互抵消，导致系统总动量守恒。即在没有外部作用力的情况下，系统的总动量始终保持不变。

2. 正则角动量守恒：当系统不受外力矩作用时，系统的总角动量守恒。具体来说，如果系统的总外力矩为零，那么系统的总角动量将保持不变。

3. 磁矩守恒：磁矩是描述物体磁性质的物理量，它在没有外部磁场的情况下保持不变。当一个物体在外部磁场中发生翻转或转动时，其总磁矩是保持不变的。

4. 磁电路：磁电路是由磁性材料和导体构成的电路系统，其中磁性材料的磁性能够对电流产生影响。磁电路包括铁心电感应线圈、电机、变压器等电子设备。

磁电路的主要特点是磁通的封闭性和磁场强度的非线性。通过磁电路的分析可以探讨磁场分布、磁阻、磁通量等。

动磁场问题指的是同时存在电场和磁场的情况下的物理现象。电场和磁场在空间中相互作用，这种相互作用由麦克斯韦方程组描述。当电荷产生电场时，会对其他电荷施加电场力；

同样，电流产生磁场时，会对其他电流施加磁场力。动磁场问题包括电磁波的传播、电荷在磁场中的受力、磁感应现象等。

电场和磁场相对论变换指的是当观察者的参考系发生运动时，电场和磁场的表现会发生变化。

根据相对论理论，电场和磁场并不是相互独立的，而是统一的电磁场。

因此，当观察者的参考系发生相对运动时，电场和磁场的表现会按照洛伦兹变换互相转换。

电磁感应建模问题涉及到电磁感应现象。当一个闭合电路中的磁通量发生变化时，会在电路中产生感应电动势，导致电流产生。这个现象由法拉第电磁感应定律描述。

在建模电磁感应问题时，需要考虑磁场的分布、电路的几何形状以及材料的电磁特性。

通过电磁感应建模，可以分析感应电流的大小和方向，以及对电路和设备的影响。

总的来说，动磁场问题、电场磁场相对论变换和电磁感应建模问题都涉及到电磁学和相对论物理的重要理论和实际应用。在解决这些问题时，需要考虑磁场和电场的相互作用，并使用相关方程，比如麦克斯韦方程组，来描述电磁现象。

同时，相对论的观点也需要被考虑，以便在不同惯性系中解释和分析电场和磁场的行为。

在电磁感应建模问题中，需要考虑磁通量、电动势和感应电流的关系，同时还需要考虑电路的几何形状和材料的特性。电磁感应建模在工程和科学领域中有广泛的应用，比如在发电机、变压器和传感器的设计中。

总之，电磁学和相对论理论是解决动磁场问题、电场磁场相对论变换和电磁感应建模问题的重要基础，它们对我们理解自然界和应用到现实生活中的技术和设备有着深远的影响。

在线性微分方程在电磁学中有着广泛的应用。电磁学的基本原理是通过麦克斯韦方程组描述电磁场的行为，而这些方程组本质上就是一组线性微分方程。

在电磁学中，线性微分方程被用来描述电场和磁场的分布、变化和相互作用。例如，库仑定律描述了两个电荷之间的相互作用力，这可以用线性微分方程形式来表达。

另一个例子是电磁波的传播，这也可以通过线性微分方程进行描述。麦克斯韦方程组中的时变电场和磁场可以被表示为线性微分方程的解。

此外，线性微分方程还可以用来分析电路中的电流和电压的关系，从而帮助工程师设计和优化电子设备。

总之，线性微分方程在电磁学中扮演着重要的角色，帮助科学家和工程师理解和利用电磁场的行为。

二元线性递推数列在电磁学中可能用于建模和描述特定的动态系统或过程。虽然在传统电磁学理论中，二元线性递推数列可能不是主要的数学工具，但可以通过某些具体的应用来看到其潜在用途。

例如，如果研究一个复杂的电磁场系统，其中包括多个相互作用的元件或系统，可能需要考虑不同部分之间的相互影响。这种情况下，可以使用二元线性递推数列来描述各个部分之间的相互作用和动态演化。

这种数学工具可以帮助建立模型，预测系统的行为以及优化系统设计。另一个可能的应用是在天线阵列的研究中。

天线阵列是通过多个天线元素组合在一起，形成一个整体性能更强大的天线系统。

在设计和优化天线阵列时，可能需要考虑不同天线元素之间的相互作用，这时可以利用二元线性递推数列来描述天线元素之间的关系和影响。

总之，虽然二元线性递推数列并非在传统电磁学中常用的数学工具，但在某些复杂的电磁场系统建模和设计问题中，它们可能会发挥重要作用。

简正模分析是电磁学中的重要概念，它在研究电磁场分布、传播和相互作用方面发挥着关键作用。

简正模分析一般涉及求解电磁场的简正模解，并且通常与线性微分方程和边界条件紧密相关。下面我们将通过一个示例来介绍简正模分析的概念、解析方法以及拓展应用，并进行总结。

### 例题考虑一个简单情况，一个长方形的金属导体板，边界上施加一定的电磁场激励。我们希望对导体板内的电磁场分布进行简正模分析。

### 解析

1. **建立边界条件和边值问题**：   在这个例子中，我们需要考虑导体板的边界条件和边值问题。这包括施加在导体板上的电磁场激励以及导体板表面的边界条件。

2. **求解简正模**：   利用边界条件和激励，我们可以通过求解相应的边值问题来获得导体板内的简正模解。

3. **分析简正模**：   一旦简正模解求得，我们可以分析每个简正模的特征、分布和相互作用，从而理解导体板内电磁场的行为。### 拓展在

拓展方面，简正模分析可以扩展到不同形状和材料的结构中，包括圆柱体、球体、复合材料等，从而揭示它们内部电磁场的行为。

另外，简正模分析也可以进一步与其他物理现象和问题结合，例如光学中的光子晶体、声学中的声子晶体等。这样的拓展能够将简正模分析应用于更多的领域，并促进跨学科领域的研究和技术应用。

### 总结通过这个例题和解析，我们总结简正模分析的关键点：

1. **建立边界条件和边值问题**：必须首先清晰地定义结构的边界条件和施加在结构上的激励，这是简正模分析的基础。

2. **求解简正模**：通过解决边值问题，我们可以获得结构内部的简正模解。

3. **分析和应用**：一旦简正模解求得，可以分析每个简正模的特征，并将其应用于预测和优化电磁场行为、传感器设计、电磁波传播等方面。

简正模分析为我们理解和利用电磁场提供了重要的数学工具，并且在现代科学和技术中扮演着重要角色。