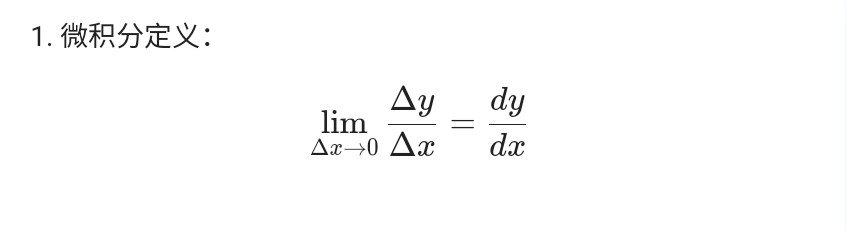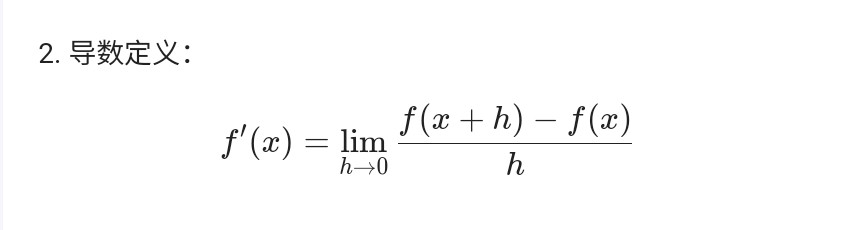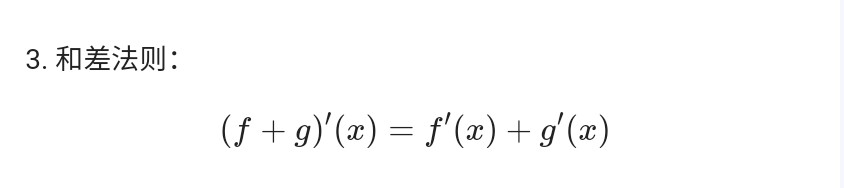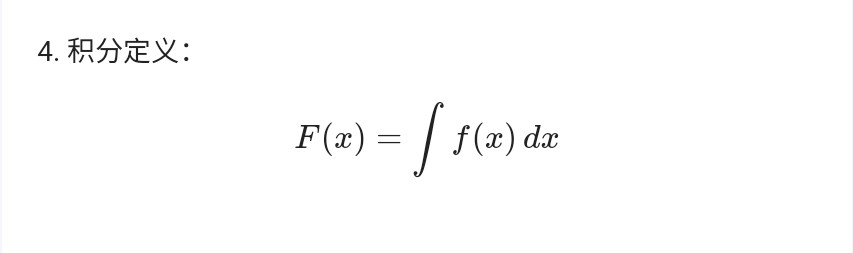物理

部分公式小结

谢谢支持

1. 热力学第一定律：$ΔU = Q - W$

1. 库仑定律：$F = k * (|q1*q2|) / r^2$

2. 电场强度与电势差关系：$E = -dV/dr$

3. 电势能公式：$U = qV$

4. 电场与电势关系：$E = -∇V$

5. 电容公式：$C = Q/V$

6. 平行板电容器的电容：$C = εA/d$

7. 电流与电荷关系：$I = ΔQ/Δt$

8. 电压与电流关系：$V = IR$

9. 欧姆定律：$V = I*R$

10. 磁场中的洛伦兹力：$F = qvBsinθ$

11. 洛伦兹力公式：$F = q(E + vB)$

12. 磁场中的回路电流磁力：$F = IlBsinθ$

13. 磁感应强度与磁通量关系：$Φ = B * A * cos(θ)$

14. 磁场中的安培定律：$∮B·dl = μ0I$

15. 磁场中的法拉第电磁感应定律：$ε = -dΦ/dt$

16. 对电路所用能量公式：$E = VIt$

17. 曼恩定律：$B = μ0 * (n * I) / L$

1. 牛顿第二定律：$F=ma$

2. 动能公式：$K = 0.5 * m * v^2$

3. 动量定理：$FΔt = Δp$

4. 万有引力定律：$F = G * (m1 * m2) / r^2$

5. 势能公式：$U = mgh$

6. 圆周运动的向心力：$F = mv^2/r$

7. 渐开线运动的加速度：$a = v^2/r$

8. 滑石运动的加速度：$a = g*sin(θ)$

9. 弹簧振子的振动周期：$T = 2π*√(m/k)$

10. 勾股定理：$a^2 + b^2 = c^2$

11. 阿基米德原理：$F_b = ρ * V * g$

12. 斯托克斯定律：$F = 6πηrv$

13. 库仑定律：$F = k * (|q1*q2|) / r^2$

14. 泰勒公式：$f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2 + ...$

15. 布拉格方程：$nλ = 2dsinθ$

16. 高斯定律：$∮E·dA = Q/ε$

17. 刚体转动惯量：$I = ∫r^2 dm$

18. 角动量定理：$τ = Iα$

19. 波速公式：$v = λf$

20. 牛顿第一定律：$ΣF = 0$

21. 弹性碰撞动能守恒定律：$K_1 + K_2 = K'_1 + K'_2$

22. 摩擦力公式：$f = μN$

23. 热力学第一定律：$ΔU = Q - W$

24. 热力学第二定律：$ΔS ≥ 0$

25. 斯内尔定律：$n1sinθ1 = n2sinθ2$

26. 马格努斯效应公式：$F_m = ρvLΓ$

27. 迈克尔逊-莫雷实验光速不变原理：$c = √(1/με)$

28. 动态平衡：$ΣF = 0 and Στ = 0$

29. 马车定理：$F = ma$

30. 波的相速度与群速度关系：$v_g = v_p - λ(dv_p/dλ)$

1. 相对论能量-动量关系$E^2 = (pc)^2 + (mc^2)^2$

2. 狭义相对论速度叠加公式$v' = (v + u) / (1 + (vu/c^2))$

3. 狭义相对论长度收缩公式$L' = L * sqrt(1 - (v^2/c^2))$

4. 狭义相对论时间膨胀公式$t' = t / sqrt(1 - (v^2/c^2))$

5. 狭义相对论质能关系$E = mc^2/ sqrt(1 - (v^2/c^2))$

1. de Broglie波长公式   $λ = h / p$

2. Heisenberg不确定性原理   $Δx * Δp ≥ h / 2π$

3. 薛定谔方程  $iħ ∂Ψ/∂t = - ħ^2/2m ∇^2 Ψ + VΨ$

4. 时间非守恒性   $[H, E] = iћ$

5. Schrödinger方程  $iћ ∂Ψ/∂t = -ћ^2/2m ∇^2 Ψ + VΨ$

6. Pauli的旋量方程   $(σ · p)Ψ = mΨ$

7. 基态能量的氢原子波函数   $E = -13.6 eV / n^2$

8. 动能与动量之间的关系   $E^2 = (pc)^2 + (m0c^2)^2$

9. 裸质子的Compton波长   $λ = h / (mc)$

10. 角动量算符的对易关系   $[Lx, Ly] = iћ$

11. 角动量取向的平方和总角动量平方的取向和   $L^2Ψ = l(l+1)ћ^2Ψ$

12. 波函数的归一化条件   $∫|Ψ|^2 dV = 1$

13. 薛定谔方程的平面波解   $Ψ(x, t) = Ae^(i(kx - ωt))$

14. 泡利不相容原理   总泡利不相容性数 = $n1 + n2 + n3 + ...$

15. 自旋角动量的取向   $S^2Ψ = s(s+1)ћ^2Ψ$

16. 定域性原理   $Ψ(r, t) = Σn CnΨn(r, t)$

18. 粒子在无限深势阱内的能级   $En = n^2h^2 / (8mL^2)$

19. 所有势能与动能的关系   $H = T + V$

20. 波函数的时间演化   $Ψ(x, t) = Ψ(x, 0) e^(-iEt/ħ)$

1. 三角函数公式：$sin^2(x) + cos^2(x) =1$

2. 对数公式：$log(ab) = log(a) + log(b)$

3. 指数公式：$a^0 = 1$

4. 二次方程根的公式： $x = (-b ± √ (b^2 - 4ac)) / 2a$

5. 直角三角形三边关系：$a^2 + b^2 = c^2$

6. 三角函数和角的关系：$sin(α ± β) = sinαcosβ ± cosαsinβ$

7. 初等数学基本定理：任何一个大于 1 的自然数，要么本身是质数，要么可以唯一地分解成质数的乘积

8. 因式分解：$a^2 - b^2 = (a + b)(a - b)$

9. 求和公式：$1 + 2 + 3 + ... + n = n(n+1)/2$

10. 迭代公式：$x_(n+1) = f(x_n)$

11. 求导法则：$(e^x)' = e^x$

12. 平行四边形面积公式：$A = bh$

13. 二项式定理：4(a + b)^n = Σ (C(n, i) * a^(n-i) * b^i)$

14. 椭圆的面积公式：$A = πab$

15. 渐近线方程：$y = mx + c$

16. 最大最小值定理：如果 $f(x)$在闭区间$[a, b]$ 上连续，那么 $f(x)$ 在这个区间上可以取得最大值和最小值

17. 柯西-施瓦茨不等式：$|⟨u, v⟩| ≤ ||u|| ||v||$

18. 泰勒公式：$f(x) = f(a) + f'(a)(x - a) + f''(a)(x - a)^2 / 2! + ... + f^(n)(a)(x - a)^n / n!$

19. 黎曼和：$Σ f(xi)Δxi$，其中 $xi$ 为分割点，$Δxi$ 为分割的长度

20. 向量叉乘公式：$|a × b| = |a||b|sinθ$

宇宙第一速度（也称为逃逸速度）是指一个物体需要具有的速度，才能够克服引力场的束缚，逃离天体表面并进入宇宙空间。在地球上，宇宙第一速度大约是11.2公里/秒。

要推导宇宙第一速度，我们可以使用能量守恒定律和动能定理来进行计算。假设一个物体从地球表面射出，我们可以将其总机械能等于零（为了逃脱地球引力场）。

我们可以使用下面的公式来计算物体的逃逸速度：

总机械能 = 动能 + 势能 = $0$

动能 = $1/2 * m * v^2$

势能 = $-G * (m*M) / r$

其中，$m$是物体的质量，$v$是物体的速度，$G$是引力常数，$M$是地球的质量，$r$是地球的半径。

通过将机械能设置为零，我们可以解出v的值，即逃逸速度的大小。这个过程可以用来推导出地球或其他天体的逃逸速度。最终，我们得到的结论是，逃逸速度取决于天体的质量和半径，以及物体的质量。

三角函数公式：

1. 正弦函数的定义：$sin(θ)$ = 对边/斜边

2. 余弦函数的定义：$cos(θ)$= 邻边/斜边

3. 正切函数的定义：$tan(θ)$ = 对边/邻边

4. 余切函数的定义：$cot(θ)$ = 邻边/对边

5. 正割函数的定义：$sec(θ)$ = 斜边/邻边

6. 余割函数的定义：$csc(θ)$ = 斜边/对边

7. 正弦函数和余弦函数的关系：$sin²(θ) + cos²(θ) = 1$

8. 正切函数和余切函数的关系：$tan(θ) * cot(θ) = 1$

9. 正切函数与正割函数的关系：$1 + tan²(θ) = sec²(θ)$

10. 余切函数与余割函数的关系：$1 + cot²(θ) = csc²(θ)$

11. 任意角的三角函数公式：$sin(-θ) = -sin(θ)$，$cos(-θ) = cos(θ)$，$tan(-θ) = -tan(θ)$，$cot(-θ) = -cot(θ)$，$sec(-θ) = sec(θ)$,$csc(-θ) = -csc(θ)$

12. 同角三角函数的相互关系：$sin(θ) = cos(90° - θ)$，$cos(θ) = sin(90° - θ)$，$tan(θ) = cot(90° - θ)$，$cot(θ) = tan(90° - θ)$

13. 任意角的两倍角公式：$sin(2θ)= 2sin(θ)cos(θ)$，$cos(2θ) = cos²(θ) - sin²(θ)$，$tan(2θ) = 2tan(θ) / (1 - tan²(θ))$

14. 任意角的半角公式：$sin(θ/2)= ±√((1 - cos(θ)) / 2)$，$cos(θ/2) = ±√((1 + cos(θ)) / 2)$，$tan(θ/2) = ±√((1 - cos(θ)) / (1 + cos(θ))$

15. 余切函数的和差化积公式：$tan(α ± β) = (tan(α) ± tan(β)) / (1 ∓ tan(α)tan(β))$

16. 余弦函数的和差化积公式：$cos(α ± β) = cos(α)cos(β) ∓ sin(α)sin(β)$

17. 任意角的倍角公式：$sin(2θ) = 2sin(θ)cos(θ)$，$cos(2θ) = cos²(θ) - sin²(θ)$

18. 任意角的和差化积公式：$sin(α + β) = sin(α)cos(β) + cos(α)sin(β)$，$sin(α - β) = sin(α)cos(β) - cos(α)sin(β)$

19. 任意角的和差化积公式：$cos(α + β) = cos(α)cos(β) - sin(α)sin(β)$，$cos(α - β) = cos(α)cos(β) + sin(α)sin(β)$

1. 常数函数导数公式：$f(x) = c$，导数为$f'(x) = 0$

2. 幂函数导数公式：$f(x) = x^n$，导数为$f'(x) = nx^(n-1)$

3. 指数函数导数公式：$f(x) = e^x$，导数为$f'(x) = e^x$

4. 对数函数导数公式：$f(x) = ln(x)$，导数为$f'(x) = 1/x$

5. 三角函数导数公式：$sin(x)$的导数为$cos(x)$，$cos(x)$的导数为$-sin(x)$，$tan(x)$的导数为$sec^2(x)$

6. 反三角函数导数公式：$arcsin(x)$的导数为$1 / √(1 - x^2)$，$arccos(x)$的导数为$-1 / √(1 - x^2)$，$arctan(x)$的导数为$1 / (1 + x^2)$

7. 和差求导法则：$(f(x) ± g(x))' = f'(x) ± g'(x)$

8. 积分求导法则：$(f(x) * g(x))' = f'(x) * g(x) + f(x) * g'(x)$

9. 商求导法则：$(f(x) / g(x))' = (f'(x) * g(x) - f(x) * g'(x)) / (g(x))^2$

10. 链式法则：若$y = f(g(x))$，则$y' = f'(g(x)) * g'(x)$

1.  常数的极限：$lim(c) = c$，其中 c 是常数

2. 极限的唯一性：如果一个函数 $f(x)$在点 $x = a$处有极限 L，则该极限唯一

3. 无穷大极限：$lim(x→∞) x^n = +∞ 或 -∞$，其中 n 是正整数

4. 夹逼定理：如果函数 $g(x) ≤ f(x) ≤ h(x)$ 在点 x = a 的某个去心邻域内成立，且 $lim(x→a) g(x) = lim(x→a) h(x) = L$ ，则 $lim(x→a) f(x) = L$

5. 函数与常数的极限：$lim(x→a) c = c$，其中 c 是常数

6. 四则运算法则：若 $lim(x→a) f(x) = A$且 $lim(x→a) g(x) = B$，则 $lim(x→a) [f(x) ± g(x)] = A ± B$，$lim(x→a) [f(x) * g(x)] = A * B$，$lim(x→a) [f(x) / g(x)] = A / B$（若 B）不等于0。

7. 复合函数的极限：若 $lim(x→a) g(x) = b$且 $lim(y→b) f(y) = L$，则 $lim(x→a) f(g(x)) = L$

8. 三角函数极限：$lim(x→0) sin(x)/x = 1$，$lim(x→0) (1 - cos(x))/x = 0$

9. 自然对数极限：$lim(x→0) (e^x - 1)/x = 1$

10. 对数函数极限：$lim(x→1) (log_a(x))/(x - 1) = 1/log(a)$，其中 a > 0 且 a ≠ 1