- 1
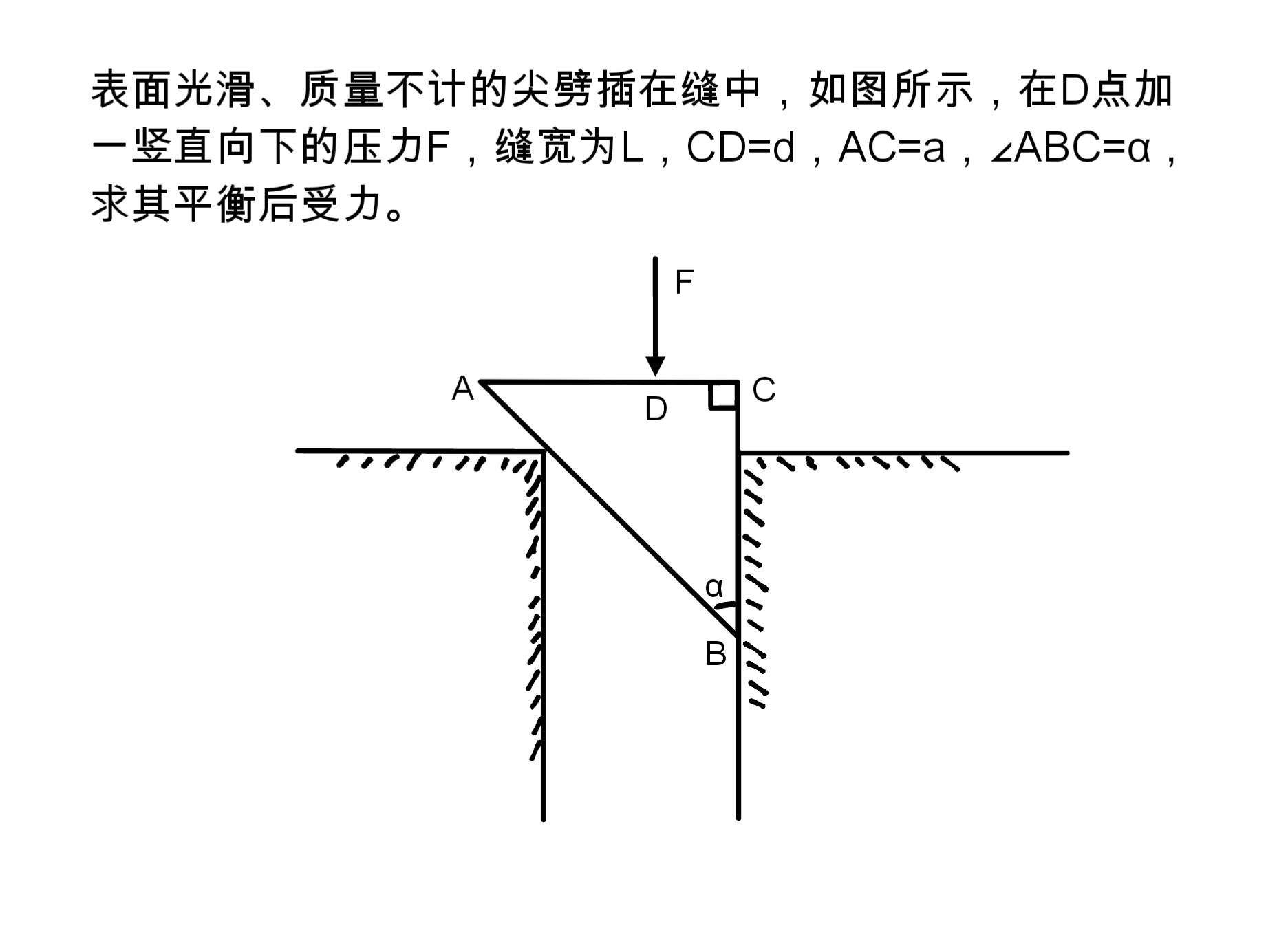
设AB与墙接触点P，P点受力垂直AB，作用在P点。BC面受力水平向左，作用点未知，但可以等效在BC上某个点。
列三个方程1.x方向受力 2.y方向受力 3.对P点力矩
三个未知数(两个力，一个作用点)可解
不要忘记在答案里注明力的三要素。。。
似乎就是这样
问题是，它受力之后就会转动，变成下面这个样子
它转过的角度θ我就死活求不出来
如果这么说的话，F 作用的位置要进行分类讨论，作用点偏左不会转，偏右会转，要通过力矩来进行判断
偏左也会转吧
呃啊不对。。话说真的会转吗
诶对，现在感觉好像不会转，因为右侧墙会对三角形有一个力矩，使产生逆时针转的效果，抵消左侧力和压力的效果
如果以右侧接触点为支点，确实也是能够平衡的，嘶～～～，那不会转？？？
是滴！实际上就是三力汇交，d小于L会转，d大于L就不会转了
就如果作用点是图上这个的话，不转是不可能的，不转的话三个力没法共点
那得分类讨论
讨论如果不转是否能三力共点
原来质量不计、表面光滑。。。那右侧的力只能水平向左，所以会转，这下应该算是解决了
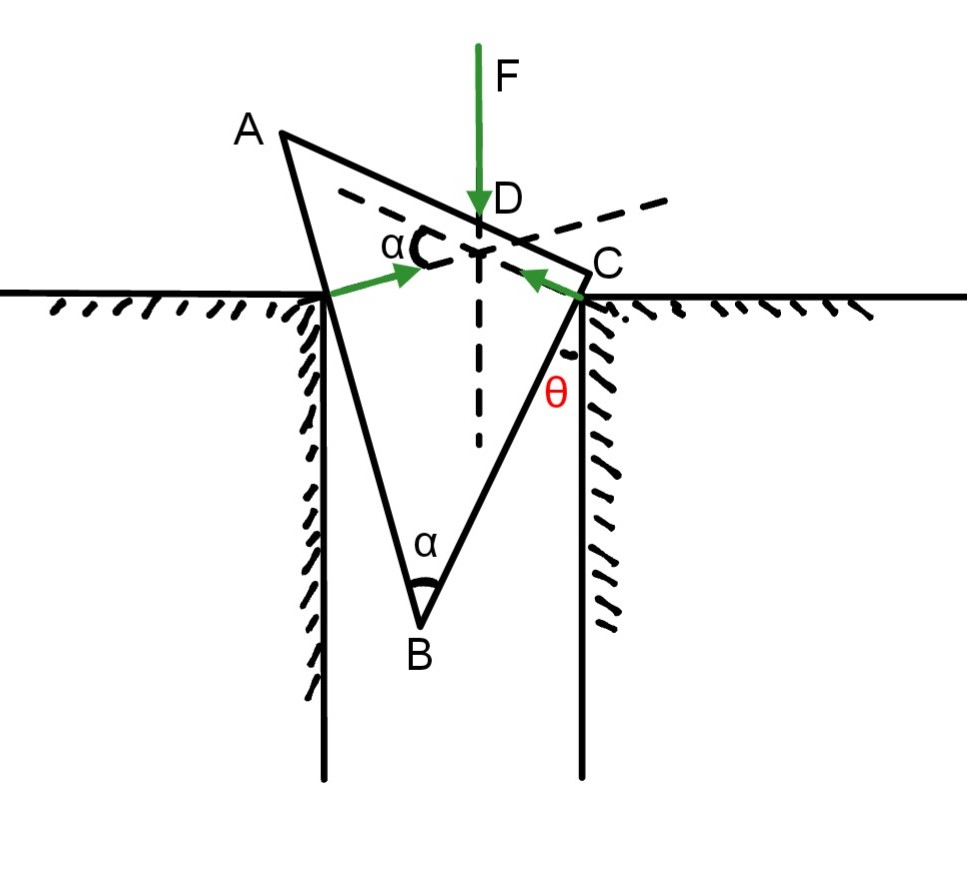
设左边、右边的支点分别为$A',C'$
先考虑受力平衡，作出力的矢量三角形，发现与$△A'BC'$相似
$F:F_{A'}:F_{C'}=L:A'B:C'B$
以B为参考点，力矩平衡
$F_{A'}\cdot A'B-F_{C'}\cdot C'B+F(BC\sin\theta-d\cos\theta)=0$
$A'B^2-C'B^2+L(\frac{a}{\tan\alpha}\sin\theta-d\cos\theta)=0$
对$△A'BC'$用正弦定理
$\frac{A'B}{\cos(\alpha-\theta)}=\frac{C'B}{\cos\theta}=\frac{L}{\sin\alpha}$
$(\frac{L\cos(\alpha-\theta)}{\sin\alpha})^2-(\frac{L\cos\theta}{\sin\alpha})^2+L(\frac{a}{\tan\alpha}\sin\theta-d\cos\theta)=0$
$\frac{L\cos^2(\alpha-\theta)}{\sin\alpha}-\frac{L\cos^2\theta}{\sin\alpha}+(a\cos\alpha\sin\theta-d\sin\alpha\cos\theta)=0$
$-L\sin(\alpha-2\theta)+(a\cos\alpha\sin\theta-d\sin\alpha\cos\theta)=0$
θ解不出来，但是可以已知θ求L,a或d
谢谢！得到最后那个方程就已经够了
不过正弦定理那里前两个角度是不是反了
佬太强了🤓
佬太强了🤓
佬太强了🤓
佬太强了🤓
$\sin(90°-\theta)=\cos\theta$
应该对的吧
$A'B$对的是右边的角，$C'B$对的是左边的角呀
是不是应该$\frac{A'B}{cos\theta}=\frac{C'B}{cos(\alpha-\theta)}
$\frac{A'B}{cos\theta}=\frac{C'B}{cos(\alpha-\theta)}$
是的，我太菜了
最后是$L\sin(\alpha-2\theta)+(a\cos\alpha\sin\theta-d\sin\alpha\cos\theta)=0$
不至于不至于，一点笔误而已
还是大佬这个相似和正弦用得妙