共11条回复
时间正序
- 时间正序
- 时间倒序
- 评论最多
三等分的伊文斯.离
1年前
2024-2-15 08:06:23
就是你下面那个图啊,画一个直角三角形,然后再以斜边为半径,直角三角形的那个小角做一个小扇形。
接着再作一个大一点的直角三角形,设斜边为一
一开始的那个小直角三角形的小角的对边就是sinx,小扇形的弧就是x,大直角三角形的小角的对边就是tanx
3条评论 评论
- 1
三等分的伊文斯.离
1年前
2024-2-15 08:18:40
等一下我看到你的上面写的那个纯数学的方法(圈1)那里你写的是把在x趋于0时sin x/x=1作为了前提条件。
但是如果我用洛必达法则一样可以得到它,并不是说我一定要知道当X很小的时候两者近似相等
6条评论 评论
Luminescent
1年前
2024-2-15 09:51:08
扇形的面积那个的确需要高数工具来严谨证明,好像是用积分。事实上,不止扇形的面积,小学课本上圆的面积,圆锥和圆柱的体积的计算公式都是基于直觉和实验来推导的,尽管足够简单直观,可以让小学生明白,但是难以令人信服
质心用户 2048
1年前
2024-2-15 12:46:48
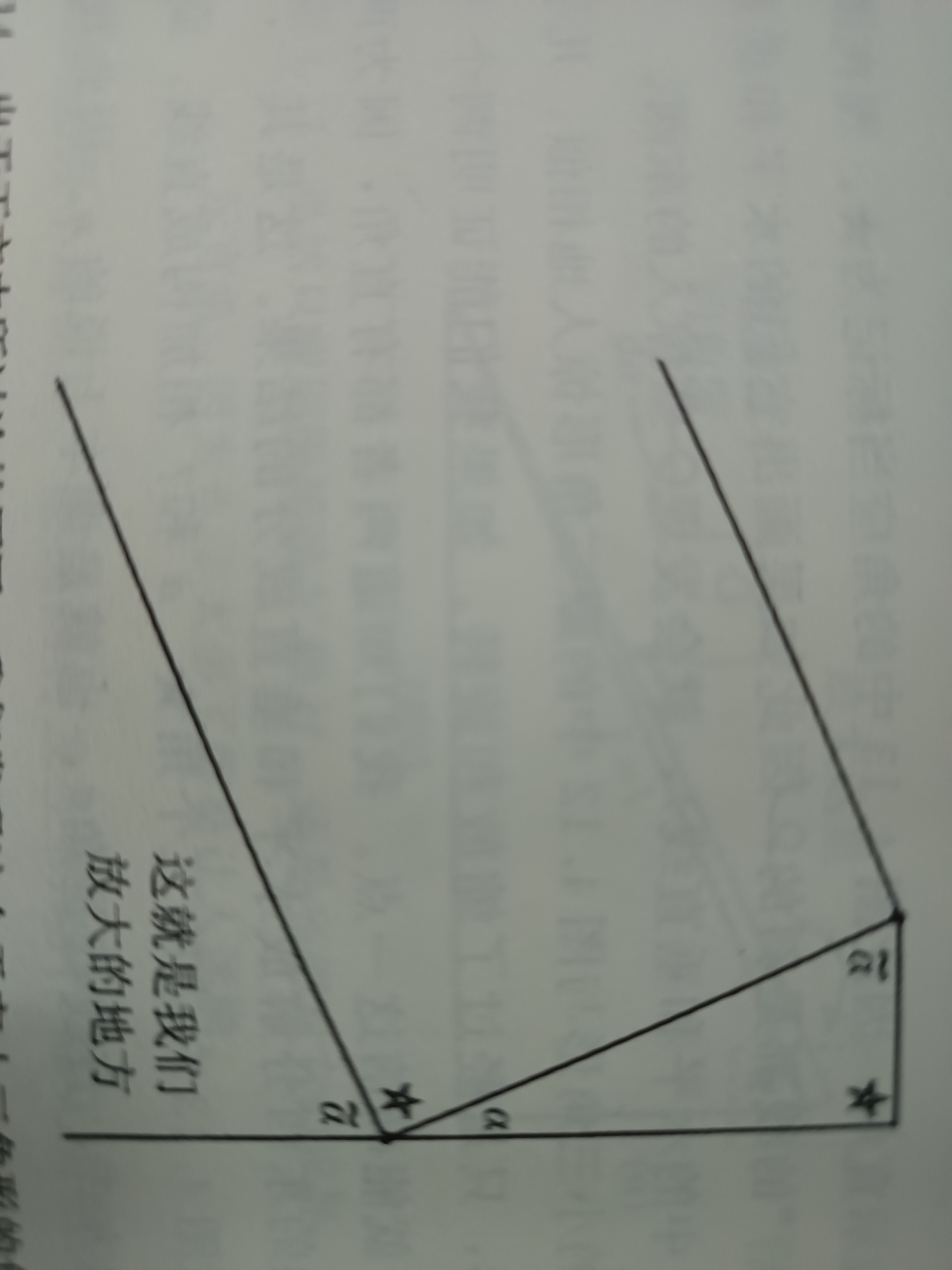
看过一本书
小角无限放大后两条半径近似平行,此时再造出一个直角三角形,可几何证明sinx导数为cosx
不知是否符合要求
2条评论 评论
8条评论 评论
Nature
1年前
2024-3-9 11:04:39
严格来说,极限是通过ε-δ语言定义的,从任意-存在的思想定义导数,并不会出现这个问题。或者像在张景中《数学家的眼光》中用不等式定义导数,完全就不需要极限的概念,也能导出Taylor公式。总结:先有sin' x=cos x, 后有sin x≈x≈tan x.
......
1年前
2024-3-11 14:34:37
我弱弱的说一句做图真的不好用吗?实在不行可以用测量啊![]() (我上课内的时候听同学讲这种原始的方法,好像我们都被思维定式困住了啊)
(我上课内的时候听同学讲这种原始的方法,好像我们都被思维定式困住了啊)
鄙人问大佬们一个问题除了矩阵等特殊运算,有什么运算(算法)是有结合律没有交换律的?
8条评论 评论
不来客
1年前
2024-3-19 23:40:59
回复@即未用户???没有,我感觉是用泰勒展开定义sinx cosx e^x,但是不会证明这个sinx就是我们认为的sinx
(板砖有点问题无法评论你的回复)
拉普拉斯的琴弦
1年前
2024-4-5 15:28:12
额,lim sin x/x=1是先用图证明出在(0,π/2)上sinx<x<tanx,再用夹逼定理证明的,没有用到小角近似啊。可以翻一翻高数课本


