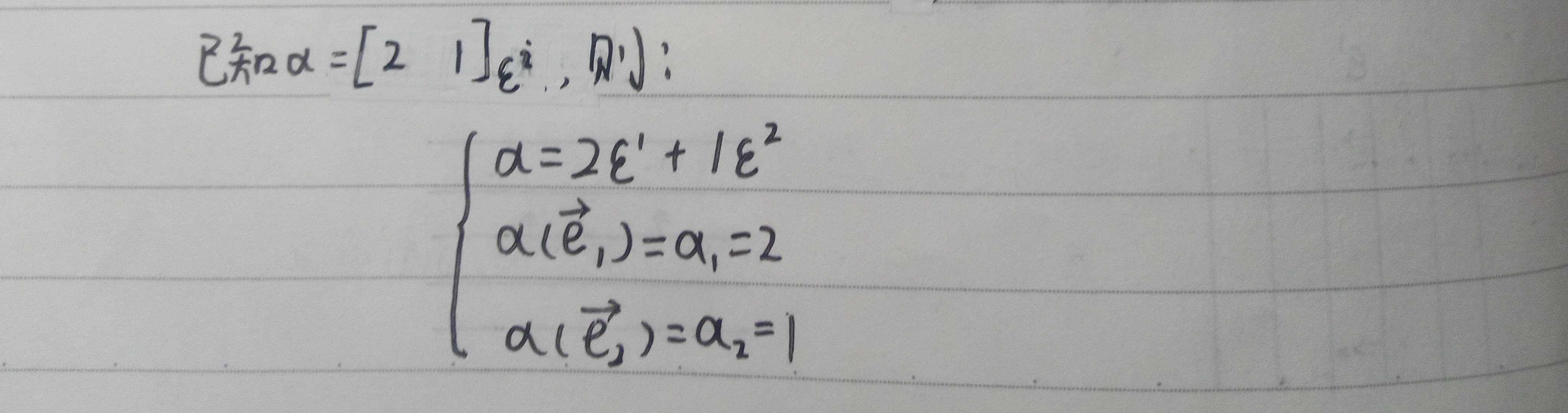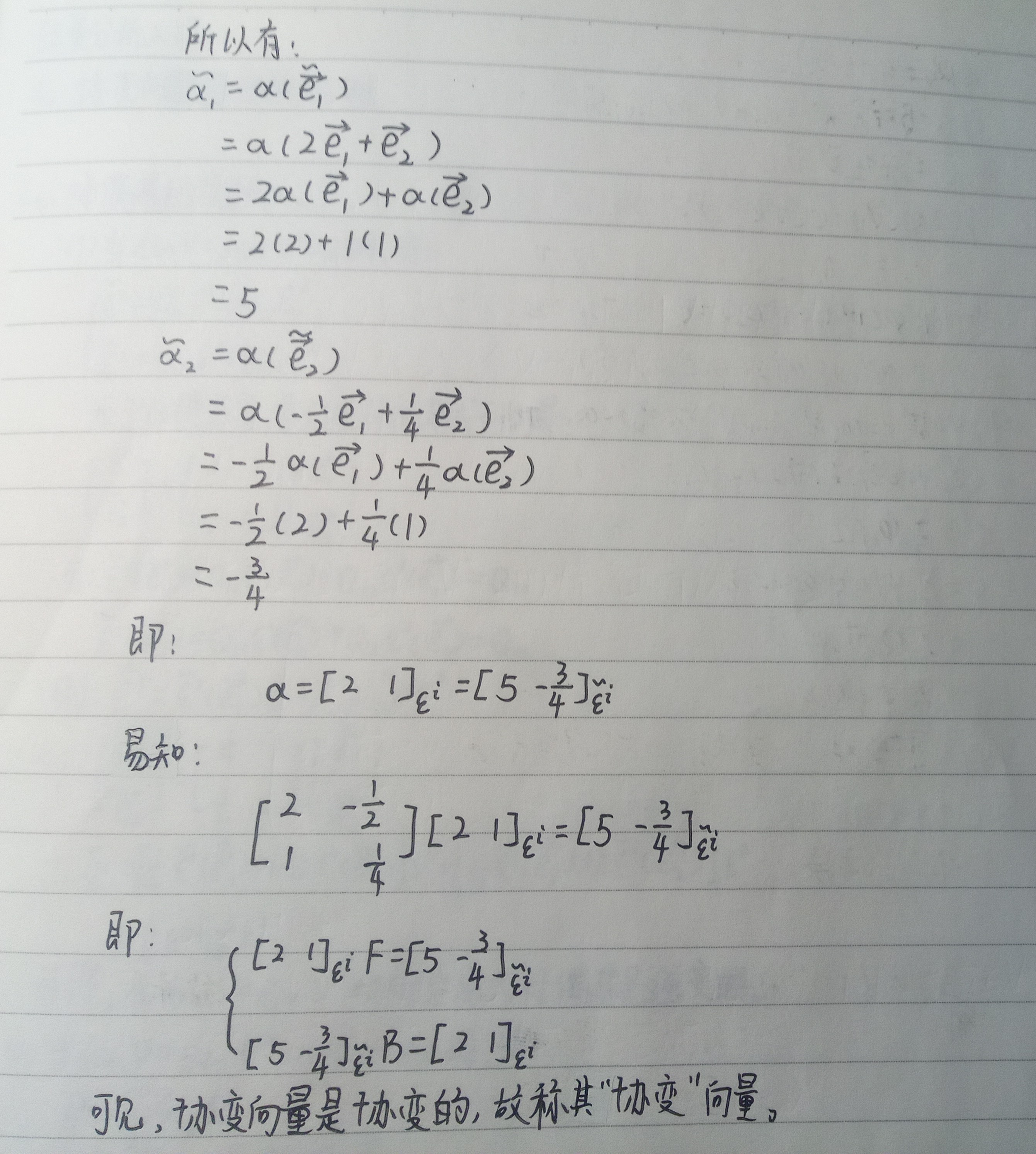物理

张量分析入门-L₅:对偶基

        上节课的时候，我们学习了协变向量。

        和向量一样，协变向量也有专属的基来描述。

        它有一个特别的名字：对偶基。

$\Huge{L_5:对偶基}$

$\Large{L_{5.1}:对偶基的概念,可视化与计算}$

        基于协变向量的定义，很明显在表示协变向量的时候，不能使用向量空间的基来描述。

        相反，我们需要用对偶空间的基来描述协变向量。所以我们引入对偶基。

        $$设现在有向量空间V，在V^*中取ε^1,ε^2…ε^n，若其满足：$$

                $$ε^i(\vec{e_j})=δ^i_j$$

        $$则称ε^1,ε^2…ε^n是对偶空间V^*的\red{对偶基(Dual\ Basis)}。$$

        在写克罗内克符号时，一个指标放在上面，一个指标放在下面，这个需要注意一下。

        因为当我们深入张量分析时，我们需要规范书写。克罗内克符号是一个张量，因此又叫克罗内克张量。在书写时，我们需要把它的一个指标放在上面，一个指标放在下面。以后我们都将使用这种方法书写克罗内克张量。

        接下来我们要干的事情，是把对偶基可视化。

        $$假设现在有向量空间V和对偶空间V^*，且满足：dim\ V=dim\ V^*=2。$$

        已知对偶$$空间V^*的对偶基为ε^1,ε^2，则对任意\vec{v}∈V，有：$$

                $$ε^1(\vec{v})=ε^1(v^1\vec{e_1}+v^2\vec{e_2})=ε^1(\vec{e_1})v^1+ε^1(\vec{e_2})v^2=v^1$$

                $$ε^2(\vec{v})=ε^1(v^1\vec{e_1}+v^2\vec{e_2})=ε^2(\vec{e_1})v^1+ε^2(\vec{e_2})v^2=v^2$$

        然后我们归纳一下结论：

                $$ε^i(\vec{v})=v^i$$

       诶，我们发现了一个有意思的点。当我们把对偶基作用在向量上，投射出了向量的分量。

       因此，对偶基长这个样：

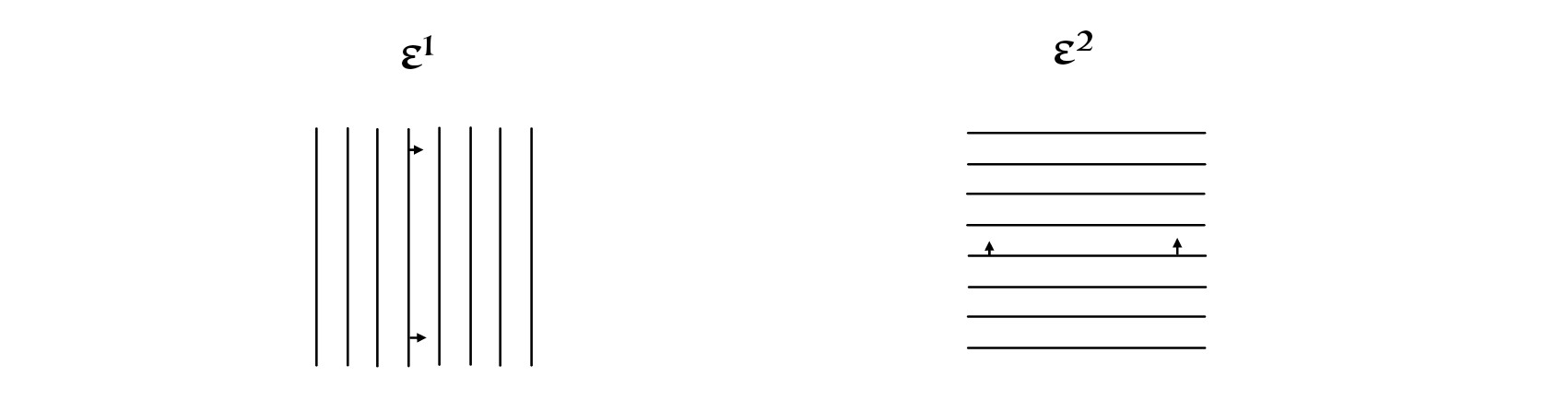
        接下来我们还要干一件事情，就是推导任意协变向量和对偶基之间的线性关系。

        在这里我们仍$$选取dim\ V=dim\ V^*=2$$的空间进行讨论。

        假设现在$有\vec{v}∈V,φ∈V^*$，则：

                $$φ(\vec{v})=φ(v^1\vec{e_1}+v^2\vec{e_2})$$

        在之前，我们已经推导$$出ε^1(\vec{v})=v^1,ε^2(\vec{v})=v^2$$，所以：

                $$φ(v^1\vec{e_1}+v^2\vec{e_2})=φ(ε^1(\vec{v})\vec{e_1}+ε^2(\vec{v})\vec{e_2})$$

        然后我们利用协变向量的线性化简这个式子之后得到：

                $$φ(ε^1(\vec{v})\vec{e_1}+ε^2(\vec{v})\vec{e_2})=φ(\vec{e_1})ε^1(\vec{v})+φ(\vec{e_2})ε^2(\vec{v})$$

        这里我们补上一个定义：$$φ(\vec{e_1})=φ_1,φ(\vec{e_2})=φ_2$$。所以，上面这个式子可以写为：

                $$φ(\vec{e_1})ε^1(\vec{v})+φ(\vec{e_2})ε^2(\vec{v})=φ_1ε^1(\vec{v})+φ_2ε^2(\vec{v})$$

        所以我们可以得到：

                $$φ(\vec{v})=\vec{v}(φ_1ε^1+φ_2ε^2)$$ 

       两边$$消去\vec{v}$$后得到：

               $$φ=φ_1ε^1+φ_2ε^2$$

       如果我们协变向量推广到更高的维度，我们就可以用求和符号写出上面的式子：

               $$φ=\sum_{i=1}^n φ_iε^i$$

       如此可见，对偶基的本质就是对偶空间的基，并且用它可以构成对偶空间中全部的协变向量。

       在本课的最后，我们补充一个之前遗漏的表示方法。众所周知，无论是向量还是协变向量，在基进行变换的时候，它的分量都会有所变化。为了区分不同基下的向量和协变向量，如果你把向量或者协变向量展开写成矩阵的形式了，那你一定要在矩阵右下角标上你所使用的基。例如：

                $$\vec{v}=\left[\begin{array}{cc}2\\1\end{array}\right]_{\vec{e_i}}$$

                $$φ=[2\ 1]_{ε^i}$$

        如果我们继续深入张量分析，学习向量场，我们甚至可以在向量场表达式的下面写上使用的基。不过这时候，我们要把基写成偏微分的形式。比如：

                $$\vec{U}=\left[\begin{array}{cc}x+2y\\4xy\end{array}\right]_{\frac{∂\vec{R}}{∂c^i}}$$

                $$\vec{\nabla f}=\left[\begin{array}{cc}4r\\cos\ θ\end{array}\right]_{\frac{∂\vec{R}}{∂p^i}}$$

         我们现在学了这么多课了，也该留个习题了，那今天就留一个吧。

                 $\blue{习题：不知道你是否还记得第二课刚开始的时候我们用来举例的旧基和新基。如果你忘了，就去翻一翻第二课。}$

                 $\blue{现在我们有一个处在旧基下的协变向量：α=[2\ 1]_{ε^i}}$

                 $\blue{试求这个协变向量在新基下的表达式。}$

                 $\blue{（提示：这一题不能直接使用协变向量的协变性来解题，而是需要使用对偶基）}$

         如果你写完了，你可以在下方评论区发表你的答案。至于标准答案……会公布的，但公布时间待定。

         好了，说了这么多，第五课也算结束了。不知道你有没有注意，我在写对偶基的时候， 把指标放在了上面。这说明它是逆变的。为什么呢？我们下节课再说。