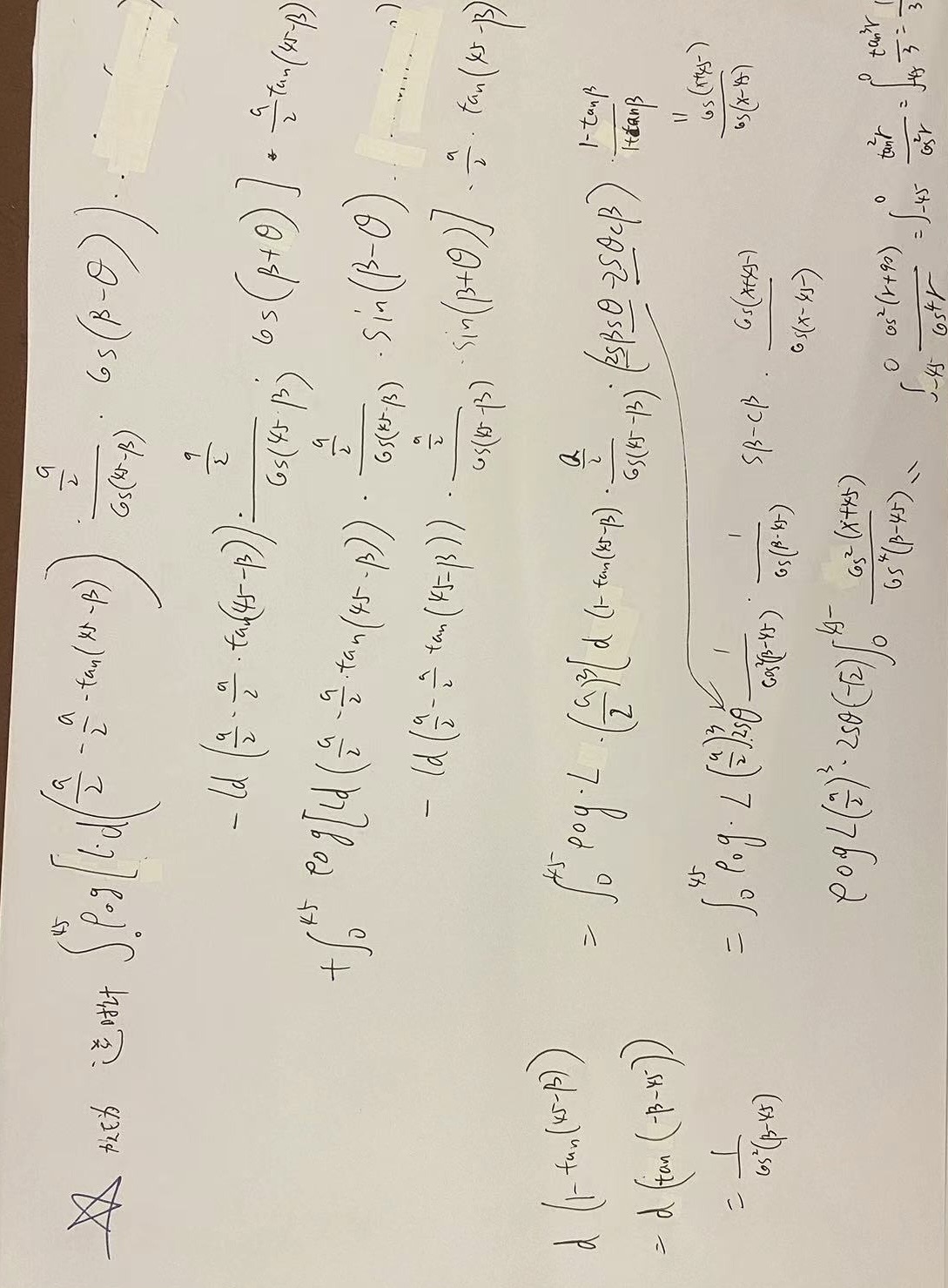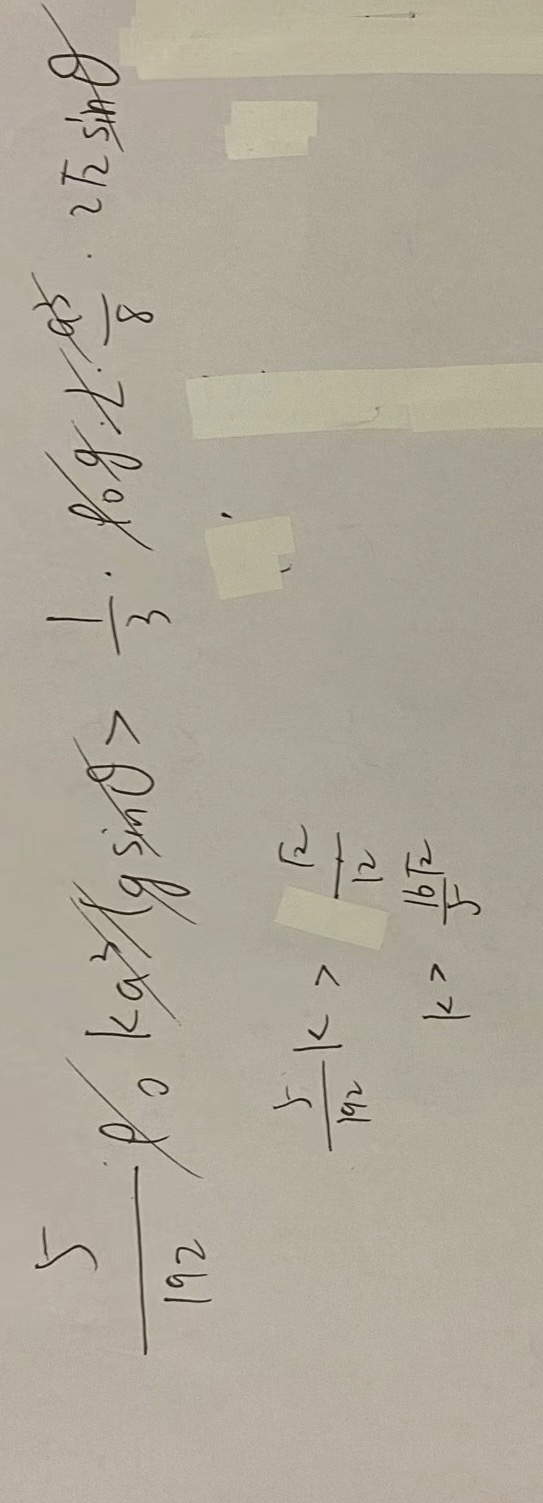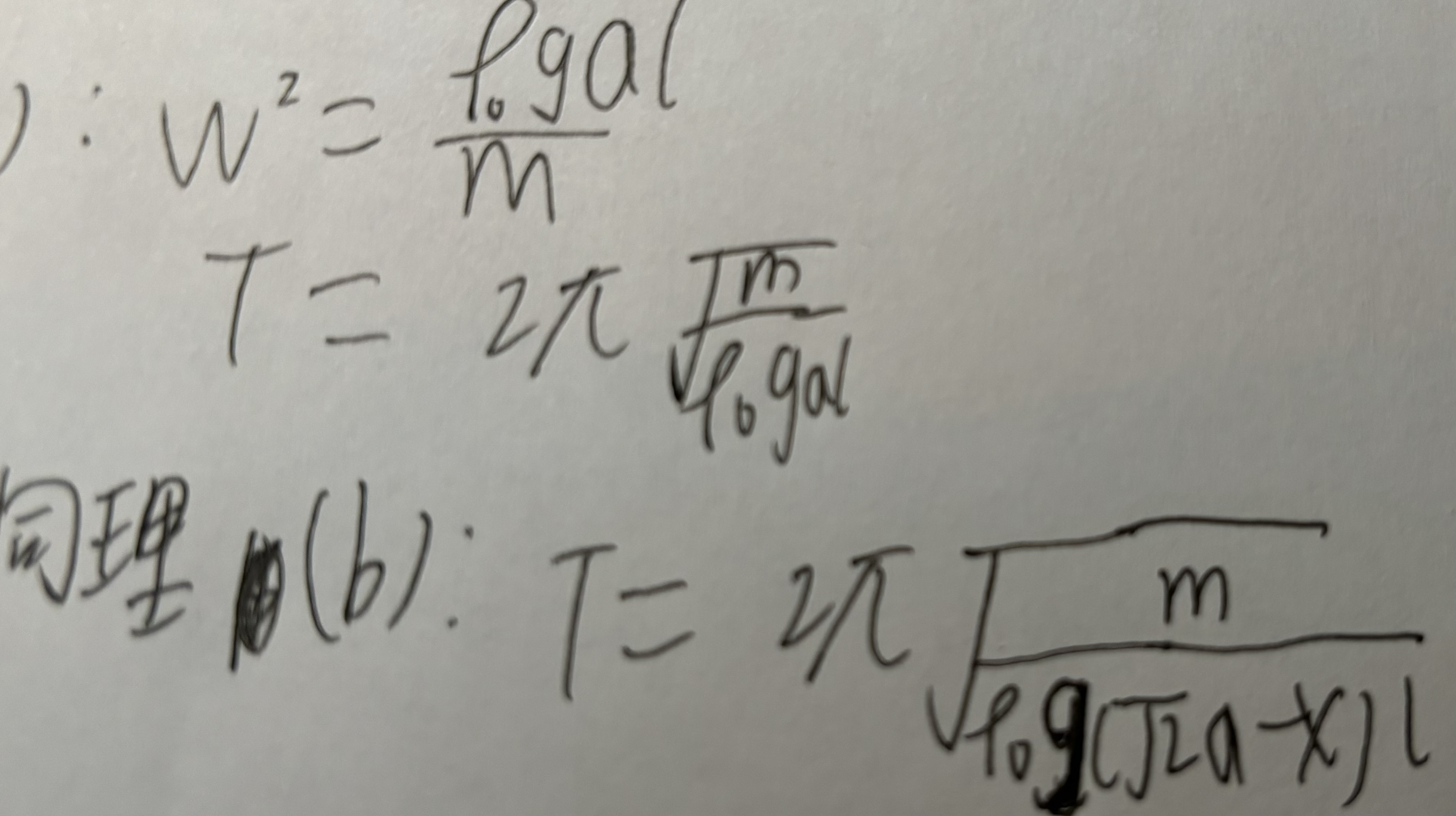（共四题，预赛难度）

Level 2 做题人数统计（截至2024/9）：共6人参与做题，第一题（引力）4人，第二题（弹力）2人，第三题（摩擦力）1人，第四题（浮力）2人

Level 2 做题建议：独立完成，将解题过程发在评论区（注意这里是Level 2，不要发错了），最好注明用时，最好再反馈一下难度

Level 2 题目评价：主要考查计算能力；第一题考查高阶小量；第二、三、四题结合几何关系进行计算，计算量较大

第一题 引力（40分）

你来到了一个奇怪的空间，万有引力与距离成α次反比，即$F=\dfrac{GMm}{r^α}$    (α>0)

如图，4个质量分别为M,M,αM,αM的质点固定在图示位置，到原点的距离均为r，原点处有一质量为m的质点

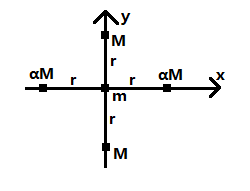
(1)（14分）若α=2，m在x方向发生微小扰动，求平衡的稳定性（偏离平衡位置时，最终能回到平衡位置是稳定平衡，会远离平衡位置是不稳定平衡，能停在偏离平衡位置是随遇平衡）

(2)（16分）若m在y方向发生微小扰动，求平衡的稳定性

(3)（10分）若撤去两个αM，m沿x轴正方向移动，求m受两个M的合力最大的位置的横坐标

第二题 弹力（40分）

如图，2根质量为M、长度为L的杆用2个等高的铰链固定在间距为L的两竖直墙壁之间

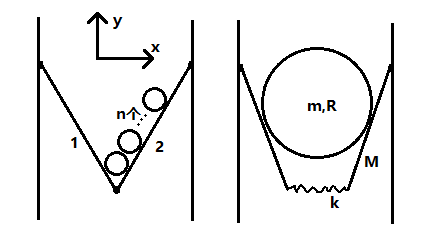
(1)（20分）若n个质量为m、半径为r的圆盘按图示放置，杆1与杆2之间也用轻质铰链连接，求杆2对杆1的作用力（用x,y分量表示）

(2)（20分）若质量为m、半径为R的圆盘按图示放置，杆与杆之间用原长为L/4、劲度系数为k的轻弹簧连接（圆盘与弹簧在垂直纸面方向略微错开），设平衡时杆与竖直方向的夹角为θ，求m(θ)，以及$kL≫Mg,kL≫mg$条件下θ(m)

第三题 摩擦力（40分）

如图，质量为M、长度为L的杆卡在2个质量为m、半径为r的圆盘之间，杆与圆盘之间的摩擦因数为$μ_1$，上面的圆盘固定，下面的圆盘与地面的摩擦因数为$μ_2$，A点恰好不与地面接触，所有接触点恰好不发生相对滑动，杆与地面的夹角为$θ_0$=37° $(\tanθ_0=\frac{3}{4},\tan\frac{θ_0}{2}=\frac{1}{3})$

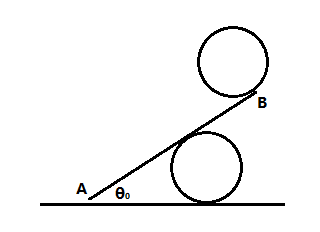
(1)（20分）求$μ_1,L,μ_2$

(2)（6分）若用铰链将A点固定在地面上，在B点施加垂直于杆的力将杆缓慢下压，使得下面的圆盘向右缓慢移动，求杆与地面夹角减小到θ的过程中圆盘相对地面自转的角度Δθ（逆时针为正）

(3)（14分）在(2)的条件下，若下压到杆与圆盘之间的接触点为B时恰好发生自锁（无论施加多大的力都不能使圆盘继续向右移动），求m（用M表示），以及杆与地面夹角为θ时需要施加的力F的大小

第四题 浮力（40分）

如图，2根长为$l$、密度为$\frac{\rho_0^{}}{2}$的木棍浮在密度为$\rho_0^{}$的水面上，木棍的横截面为边长为a的正方形

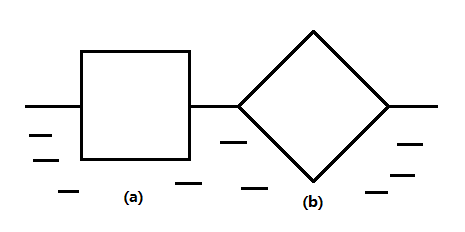
(1)（10分）若木棍在竖直方向上做小幅振动，就(a)(b)两种情况求振动周期（已知：若质量为m的物体受到的合力与位移的关系为$\vec{F}=-k\vec{x}$，则振动周期为$2\pi\sqrt{\frac{m}{k}}$）

(2)（18分）若木棍绕质心发生微小转动，通过计算说明，哪个是稳定平衡？

(3)（12分）对于不稳定平衡的木棍，要通过改变其密度分布使其变为稳定平衡，设改变后的密度分布只与初始位置到水面的高度y（向上为正）有关，即$\rho=\frac{\rho_0^{}}{2}(1-\frac{ky}{a})$，求k的最小值

$\color{red}答案解析$

还没做题的不要往下翻！

第一题 引力（40分）

(1)（14分）

设质点沿x方向偏离dx距离，则质点受到x方向的合力

$F=\dfrac{G(2M)m}{(r-\mathrm{d}x)^2}-\dfrac{G(2M)m}{(r+\mathrm{d}x)^2}-2\cdot\dfrac{GMm}{r^2+\mathrm{d}x^2}\cdot\dfrac{\mathrm{d}x}{\sqrt{r^2+\mathrm{d}x^2}}$  （4分）

保留一阶小量，得

$F=\dfrac{G(2M)m}{r^2}(1+\dfrac{2\mathrm{d}x}{r})-\dfrac{G(2M)m}{r^2}(1-\dfrac{2\mathrm{d}x}{r})-2\cdot\dfrac{GMm}{r^3}\mathrm{d}x$  （4分）

化简，得

$F=\dfrac{6GMm}{r^3}\mathrm{d}x$  （4分）

$\dfrac{6GMm}{r^3}\gt0$，即F与dx方向相同，质点受到x方向的合力会使质点远离平衡位置，是不稳定平衡  （2分）

(2)（16分）

设质点沿y方向偏离dy距离，则质点受到y方向的合力（注意(1)中的α=2在后面的小题中不适用）

$F=\dfrac{GMm}{(r-\mathrm{d}y)^\alpha}-\dfrac{GMm}{(r+\mathrm{d}y)^\alpha}-2\cdot\dfrac{G(\alpha M)m}{(r^2+\mathrm{d}y^2)^{\alpha/2}}\cdot\dfrac{\mathrm{d}y}{\sqrt{r^2+\mathrm{d}y^2}}$  （4分）

保留一阶小量、二阶小量，都会得到F=0的结果，但这并不表示随遇平衡，因为F只是近似等于0  （2分）

保留三阶小量，得

$F=\dfrac{GMm}{r^\alpha}(1+\dfrac{\alpha\mathrm{d}y}{r}+\dfrac{\alpha(\alpha+1)\mathrm{d}y^2}{2r^2}+\dfrac{\alpha(\alpha+1)(\alpha+2)\mathrm{d}y^3}{6r^3})-\dfrac{GMm}{r^\alpha}(1-\dfrac{\alpha\mathrm{d}y}{r}+\dfrac{\alpha(\alpha+1)\mathrm{d}y^2}{2r^2}-\dfrac{\alpha(\alpha+1)(\alpha+2)\mathrm{d}y^3}{6r^3})-\dfrac{2\alpha GMm}{r^{\alpha+1}}(1-\dfrac{(\alpha+1)\mathrm{d}y^2}{2r^2})\mathrm{d}y$  （4分）

化简，得

$F=\dfrac{GMm}{3r^3}\alpha(\alpha+1)(\alpha+5)\mathrm{d}y^3$  （4分）

因为α>0，所以$\dfrac{GMm}{3r^3}\alpha(\alpha+1)(\alpha+5)\gt0$，即F与dy方向相同，质点受到y方向的合力会使质点远离平衡位置，是不稳定平衡  （2分）

(3)（10分）

m所在位置的横坐标为x时，受两个M的合力大小

$F=\dfrac{2GMmx}{(r^2+x^2)^{(\alpha+1)/2}}$  （2分）

当F(x)最大时，$\dfrac{\mathrm{d}F}{\mathrm{d}x}=0$  （2分）

$\dfrac{\mathrm{d}F}{\mathrm{d}x}=2GMm\cdot\dfrac{(r^2+x^2)^{(\alpha+1)/2}-x\cdot2x\cdot\frac{\alpha+1}{2}(r^2+x^2)^{(\alpha-1)/2}}{(r^2+x^2)^{\alpha+1}}$  （2分）

化简，得

$r^2=\alpha x^2$  （2分）

解得（负值舍去）

$x=\dfrac{r}{\sqrt\alpha}$  （2分）

第二题 弹力（40分）

(1)（20分）

对n个圆盘整体受力分析，得

杆1,2对圆盘的作用力大小  $N_1=N_2=nmg$  （2分）

$N_1$作用点到杆1,2连接点的距离  $x_1=\sqrt3r$  （2分）

以n个圆盘的质心为参考点

圆盘受到$N_1$的力矩  $M_1=(n-1)rN_1\sin30°$  （2分）

圆盘受到$N_2$的力矩  $M_2=[x_2-(n-1+\sqrt3)r]N_2$  （2分）

力矩平衡  $M_1+M_2=0$  （2分）

解得$N_2$作用点到杆1,2连接点的距离  $x_2=(\sqrt3+\dfrac{n-1}{2})r$  （2分）

杆1力矩平衡  $N_1(L-x_1)+Mg\dfrac{L}{4}=F_xL\cos30°+F_yL\sin30°$  （2分）

杆2力矩平衡  $N_2(L-x_2)+Mg\dfrac{L}{4}=F_xL\cos30°-F_yL\sin30°$  （2分）

解得

$F_x=\dfrac{nmg[4L-(n-1+4\sqrt3)r]+MgL}{2\sqrt3L}$  （2分）

$F_y=\dfrac{nmg(n-1)r}{2L}$  （2分）

(2)（20分）

M,m之间的作用力  $N=\dfrac{mg}{2\sin\theta}$  （2分）

弹簧弹力  $F=k(L-2L\sin\theta-\dfrac{L}{4})$  （2分）

设作用点到杆与墙连接点的距离为x

根据几何关系，得  $R\cos\theta+x\sin\theta=\dfrac{L}{2}$  （2分）

杆的力矩平衡  $Nx+Mg\dfrac{L\sin\theta}{2}-FL\cos\theta=0$  （2分）

解得

$m(θ)=\dfrac{\sin^2\theta}{g(L-2R\cos\theta)}[kL^2(3-8\sin\theta)\cos\theta-2MgL\sin\theta]$  （4分）（*）

当$M,m=0$时，  $\sin\theta_0=\frac{3}{8}$  （2分）

当$M,m$很小，分析（*）式，得$(3-8\sin\theta)$很小，设$\theta=\theta_0+\mathrm{d}\theta$，（*）式可以写成

$\mathrm{d}m=\dfrac{\sin^2\theta}{g(L-2R\cos\theta)}[-8kL^2\cos\theta\cos\theta_0\mathrm{d}\theta-2gL\sin\theta\mathrm{d}M]$  （2分）

θ在其他位置的小量变化会与小量相乘得到高阶小量，可以忽略，所以上式的θ（以及（*）式对应位置的θ）可以改为$\theta_0$

将$\sin\theta_0=\frac{3}{8}$代入（*）式，得

$m=\dfrac{9}{16g(4L-\sqrt{55}R)}[\dfrac{\sqrt{55}}{8}kL^2(3-8\sin\theta)-\dfrac{3}{4}MgL]$  （2分）

解得

$θ(m)=\arcsin\dfrac{\dfrac{3\sqrt{55}}{8}kL^2-\dfrac{16mg(4L-\sqrt{55}R)}{9}-\dfrac{3}{4}MgL}{\sqrt{55}kL^2}$  （2分）

第三题 摩擦力（40分）

(1)（20分）

圆盘力矩平衡  $f_1r=f_2r$    $\Rightarrow f_1=f_2$  （2分）

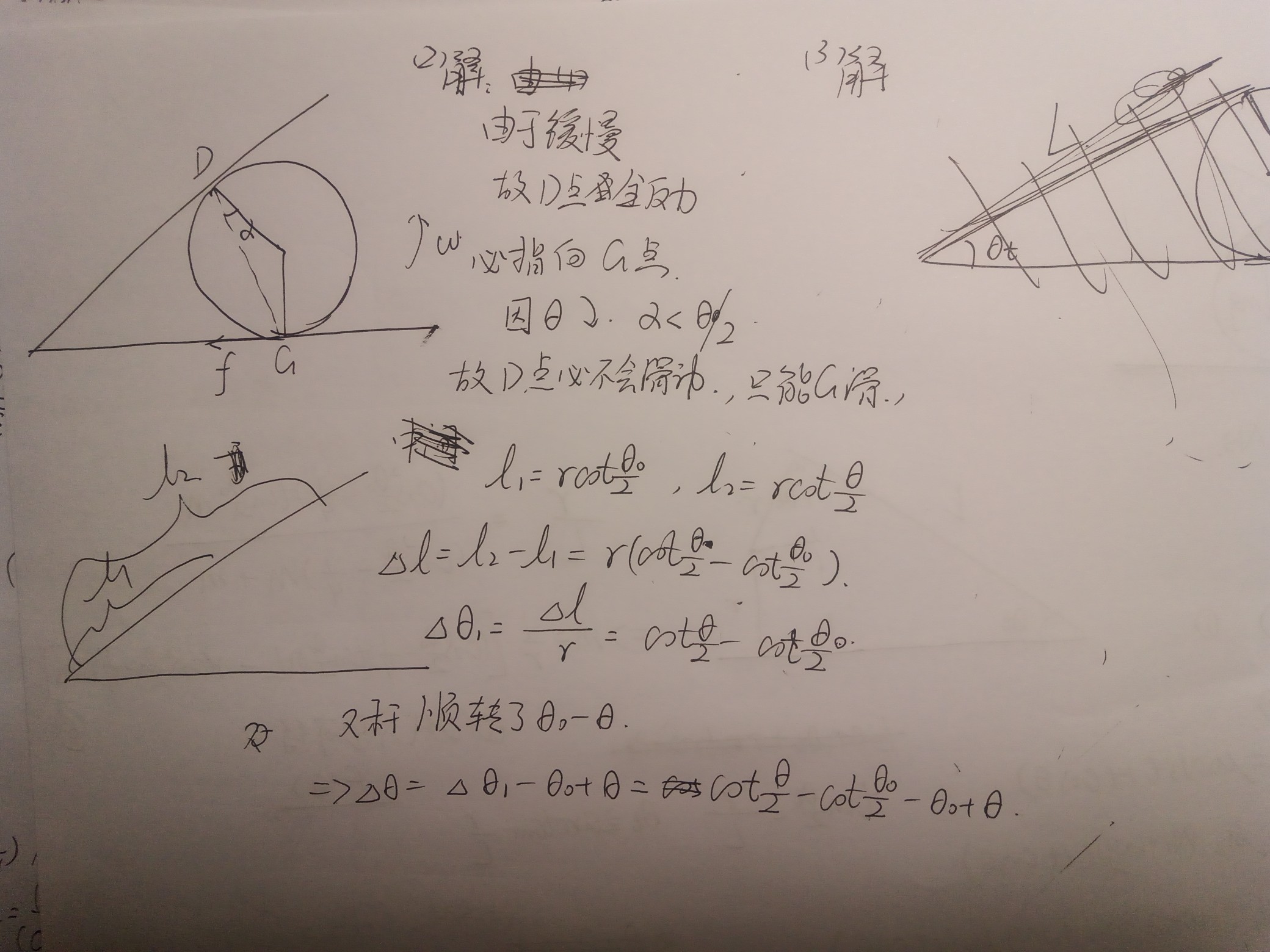
则圆盘的受力满足下图：

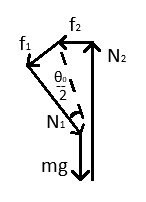
由图和角平分线的性质，得  $\mu_1=\tan\frac{\theta_0}{2}=\frac{1}{3}$  （4分）

杆受力平衡  $f_1+f_B=\mu_1(N_1+N_B)=Mg\sin\theta_0$  （1分）

$N_1=N_B+Mg\cos\theta_0$  （1分）

解得  $N_1=\frac{13}{10}Mg$  （2分）

以B为参考点，杆力矩平衡  $Mg\frac{L}{2}\cos\theta_0=N_1(L-\dfrac{r}{\tan\frac{\theta_0}{2}})$  （2分）

解得  $L=\frac{13}{3}r$  （2分）

由图和角平分线的性质，得  $N_2=mg+N_1$  （3分）

则  $\mu_2=\dfrac{f_2}{N_2}=\dfrac{f_1}{N_2}=\dfrac{\mu_1N_1}{mg+N_1}=\dfrac{13M}{30m+39M}$  （3分）

(2)（6分）

杆与地面夹角减小，由于过程缓慢，圆盘仍然受力平衡，满足  $\dfrac{f_1}{N_1}=\tan\dfrac{\theta}{2}<\mu_1$

所以圆盘与杆间没有相对滑动，圆盘与地面间有相对滑动  （2分）

圆盘与杆的接触点在杆上移动的距离为  $\Delta l=\dfrac{r}{\tan\frac{\theta}{2}}-\dfrac{r}{\tan\frac{\theta_0}{2}}$  （1分）

圆盘相对杆自转的角度为  $\Delta\theta_r=\dfrac{\Delta l}{r}=\dfrac{1}{\tan\frac{\theta}{2}}-3$  （1分）

但在这一过程中杆转了（负号表示顺时针）  $\Delta\theta_M=-(\theta_0-\theta)$  （1分）

所以圆盘相对地面自转的角度为（注意$\theta_0$换算成弧度制）

$\Delta\theta=\Delta\theta_M+\Delta\theta_r=\dfrac{1}{\tan\frac{\theta}{2}}-3+\theta-\dfrac{37\pi}{180}$  （1分）

(3)（14分）

接触点为B时  $\tan\dfrac{\theta_1}{2}=\dfrac{r}{L}=\dfrac{3}{13}$  （1分）

杆与地面夹角减小，由于过程缓慢，圆盘仍然受力平衡，且圆盘与地面间有相对滑动，得

$\mu_2=\dfrac{f_2}{N_2}<\tan\dfrac{\theta}{2}$

则自锁条件为  $\mu_2=\tan\dfrac{\theta_1}{2}=\dfrac{3}{13}$  （3分）

代入(1)中求出的$\mu_2$，得  $m=\frac{26}{45}M$  （2分）

再根据圆盘的受力图，得

$(mg+N_1')\mu_2=N_1'\tan\dfrac{\theta}{2}$  （2分）

解得  $N_1'=\dfrac{26Mg}{15(13\tan\frac{\theta}{2}-3)}$  （2分）

以A为参考点，杆力矩平衡  $N_1'\dfrac{r}{\tan\frac{\theta}{2}}=FL+Mg\frac{L}{2}\cos\theta$  （2分）

解得  $F=(\dfrac{2}{5\tan\frac{\theta}{2}(13\tan\frac{\theta}{2}-3)}-\dfrac{\cos\theta}{2})Mg$  （2分）

第四题 浮力（40分）

(1)（10分）

木棍的密度为$\frac{\rho_0^{}}{2}$，则木棍的质量  $m=\frac{\rho_0^{}}{2}a^2l$  （2分）

竖直方向偏离平衡位置的位移为$\vec{h}$时，合力等于浮力的变化  $\Delta F=-\rho_0^{}g\Delta V=-\rho_0^{}gSh$  （2分）

于是有  $k=\rho_0^{}gS$  （1分）

其中$S$为木棍被水面截得的面积， $S_a=al$ ， $S_b=\sqrt2al$  （1分）

代入公式，得

$T_a=\pi\sqrt{\dfrac{2a}{g}}$  （2分）

$T_b=\pi\sqrt{\dfrac{\sqrt2a}{g}}$  （2分）

(2)（18分）

设木棍由状态(a)顺时针转了θ角

如图，将木棍没入水面以下的部分分为1,2两部分

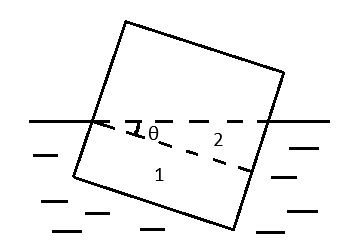
排开水的体积

$V_1=a\dfrac{a-a\tan\theta}{2}l$  （2分）

$V_2=\frac{1}{2}a^2\tan\theta\cdot l$  （2分）

浮力的作用点（排开水的质心）与木棍中心的水平距离

$x_1=(\dfrac{a-a\tan\theta}{4}+\dfrac{a\tan\theta}{2})\sin\theta$  （2分）

$x_2=-\dfrac{1}{3}\cdot\dfrac{a}{2\cos\theta}\cos2\theta$  （2分）

根据浮力的力矩公式  $M=x\rho_0^{}gV$  （2分）

代入，得（以木棍中心为参考点，顺时针为正）

$M_1=\rho_0^{}ga^3l\sin\theta\dfrac{1-\tan^2\theta}{8}$  （2分）

$M_2=-\rho_0^{}ga^3l\tan\theta\dfrac{\cos2\theta}{12\cos\theta}=\rho_0^{}ga^3l\sin\theta\dfrac{1-\tan^2\theta}{12}$  （2分）

对任意 $0\le\theta\le\frac{\pi}{4}$，有  $M_1+M_2\gt0$  （2分）

（当θ略小于0或略大于$\frac{\pi}{4}$时，$M_1+M_2\lt0$）

所以木棍将顺时针旋转，当 $\theta\to0$ 时，相当于从(a)顺时针偏离平衡角度，所以(a)是不稳定平衡；  （1分）

当 $\theta\to\frac{\pi}{4}$ 时，相当于从(b)逆时针偏离平衡角度，所以(b)是稳定平衡  （1分）

(3)（12分）

木棍(a)是不稳定平衡，由于浮力及其力矩与木棍的密度分布无关，则木棍受到浮力的力矩为

$M_F=M_1+M_2=\rho_0^{}ga^3l\sin\theta\dfrac{1-\tan^2\theta}{24}$  （2分）

当密度分布为 $\rho=\frac{\rho_0^{}}{2}(1-\frac{ky}{a})$ 时，木棍的质心到几何中心的距离为

$h=\dfrac{\int_{-a/2}^{a/2}\rho aly\mathrm{d}y}{m}=-\dfrac{k}{12}a$  （4分）

则木棍受到重力的力矩为  $M_G=-mgh\sin\theta=-\frac{k}{24}\rho_0^{}ga^3l\sin\theta$  （2分）

令 $M_F+M_G=0$，得  $k=1-\tan^2\theta$  （2分）

取 $\theta\to0$，得  $k=1$  （2分）

所以k的最小值为1

（当k=1时，$M_F+M_G=-\frac{1}{24}\rho_0^{}ga^3l\sin\theta\tan^2\theta\lt0$，也是稳定平衡）

（注：如果题目问k的取值范围，要考虑临界情况（k=1）是不是稳定平衡，可能要用到高阶小量（本题用不到）（但是临界情况不考虑或考虑错也不一定扣分，时间紧可以先不考虑）；但如果求最值，出题人要么已经把临界情况考虑好了，要么就不考虑，不需要你来考虑，这不是数学题，不会故意把答案设成不存在）

（突然发现 $k=1-\tan^2\theta$ 很像是 $k=0.999999......$ ）