物理

张量分析入门-L₄:协变向量的概念和性质与对偶空间

        在上一次课的时候，我们已经学会了向量的基础运算。

        期间我们提到，向量是一个逆变量，而且与逆变量相反的，存在协变量。

        今天这节课，我们就学习我们遇到的第二个协变量---协变向量。

$\huge{L_4：协变向量的概念和性质与对偶空间}$

$\Large{L_{4.1}：协变向量的概念}$

        当我们学习线性代数的时候，书上告诉我们，向量分为行向量和列向量。上一节课中，我们所说的向量都是指列向量，他们是逆变的。而这一节课，我们要说协变向量。

        简单来说，我们上面提到的协变向量等同于行向量。那么这是什么意思呢？仔细想一想矩阵乘法。对于任意一个行$向量φ$，和任意一个列向$量\vec{v}$，他们乘起来总会得到一个标量。所以，我们可以把行向量视作一个函数，他可以把向量映射回实数域。因为协变向量等同于行向量，所以接下来我们就可以得到协变向量的标准定义：

                $\red{协变向量(Covector)}$是一个可以将任意维数与其自身相同的向量映射到实数域的函数，简称协向量。

       通常，协向量用希腊字母表示。

       我们也可以用数学的语言表达。假$设φ$是一个协向量，则$φ满足$映射：

               $$φ:V→\mathbb{R}$$

       其中，$V是$任意的一个向量空间。从上面这个式子中，我们可以推导出协向量的计算式：

               $$φ(\vec{v})=\sum_{i=1}^n φ_i v^i$$

       这样，关于协向量的定义，基本就结束了。

$\Large{L_{4.2}：协向量的性质}$

        对于任意两个$协向量α和β$，存在以下两条性质：

                $$(1)(α+β)(\vec{v})=α(\vec{v})+β(\vec{v})$$

                $$(2)α(n\vec{v})=nα(\vec{v})=(nα)(\vec{v})$$

        当然，我们也可以把上面两条性质合在一起写：

                $$(α+β)(n\vec{v})=nα(\vec{v})+nβ(\vec{v})$$

        所以，协向量是线性的，满足线性规则。

$\Large{L_{4.3}：协向量在二维空间中的表示}$

        在上面，我们已经了解到了协向量的定义和性质。那接下来，我们就要学习协向量的表示方法。

        有同学会说，啊，这不简单吗？按照它矩阵里给出的数值，找到它的横坐标和纵坐标，走原点连一条线不就行了吗？

        事实证明，可以是可以，但是我们要区分它和正常的向量。所以，我们新找一种表示方法。我们现在假设一个$协向量φ$，和一个正常向量。我们写出他们相乘的式子：

                $$φ(\vec{v})=[φ_1\ φ_2]\left[\begin{array}{cc}x\\y\end{array}\right]$$

         很明显，我们$把\vec{v}的分量改成了x和y$，以适应坐标系。

         接下来我们$以σ=[2\ 1]$举例：

                 $$σ(\vec{v})=2x+y$$

         这时候出现了问题。我们怎么在一个纸面上画出二元函数呢？这好像是不可能的事情。

         但是，我们还是老样子，联想一下其他学科。众所周知，地理上有等高线。那我们可不可以作什么“等截距线”，来表示二元函数呢？

         我们试一下：

                 $$2x+y=0⇔y=-2x$$

                 $$2x+y=1⇔y=-2x+1$$

                 …………

                 $$2x+y=n⇔y=-2x+n$$

         然后我们构建一个坐标系，画出上$面n条$互相平行的直线，然后在他它们的上面标上截距，我们就完成了协向量的表示。

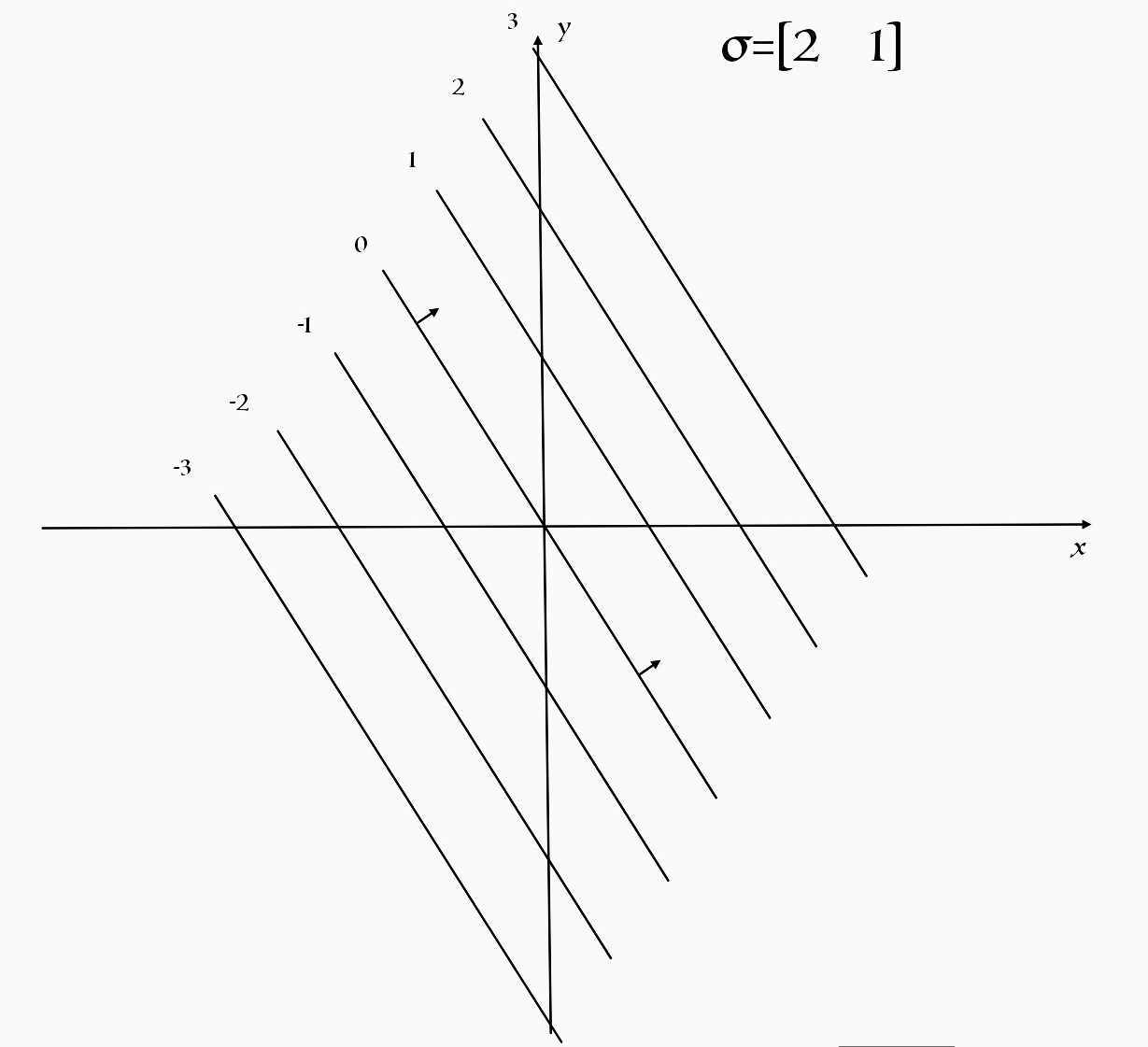
        注意我在一条线上加了两个箭头。

        这个箭头代表了协向量的方向。那么如何确定这个方向呢？很简单。我们只需要通过协向量矩阵给出的数值在坐标轴上画出这个点，然后将它与原点连一个箭头，这个箭头的方向就是协向量的方向。

        那么如何确定线与线之间的间隔呢？在这里，线与线之间的纵向间隔是一$个y轴$基向量模长。但是，这个规则只适用于第二个分量为一的协向量。如果第二个分量不为一，那么我们就需要用协向量的数乘处理。这就引出了我们下面要讲的东西。

$\Large{L_{4.4}：协向量在二维空间中的计算}$

        在上面，我们知道了协向量的表示方式。很多同学可能会感到奇怪，这画一条一条杠有什么用？其实，把协向量写成一条一条线的形式是为了计算协向量作用在普通向量上所获取的值。我们给出下面这个定理：

                $\red{穿透定理(Penetration\ Theorem)}$：对于任意一个$协变向量φ$，其作用在向$量\vec{v}$上的值等$于\vec{v}$所穿$透φ$直线的数目。

         下面我们给出一幅图，以协向$量σ$为例，解释一下上面的定理：

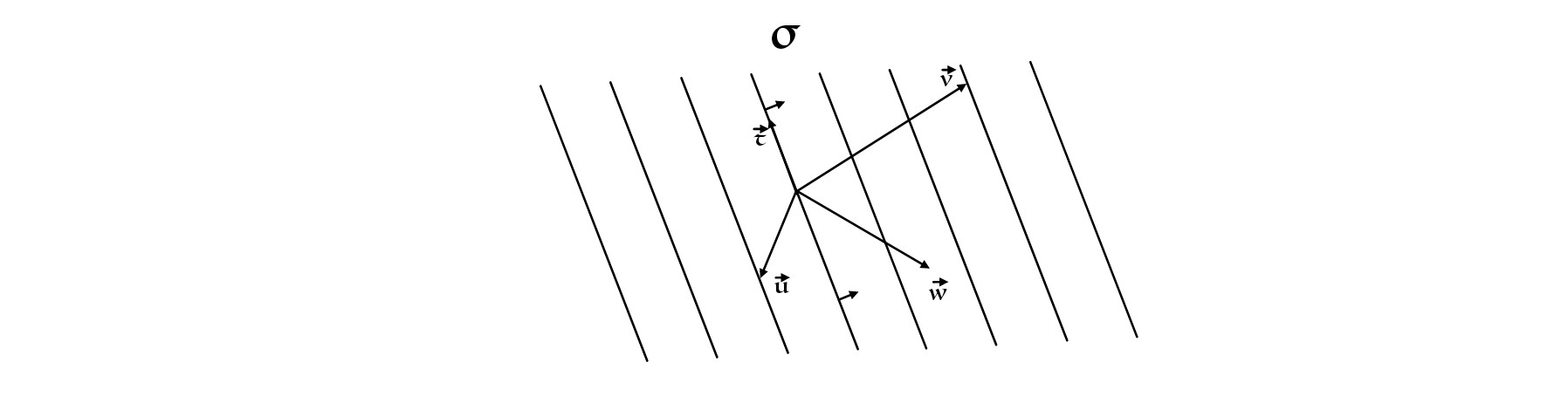
       在这幅图中，有四个向量。我们一一给$出σ$作用在他们上所获取的值：

                $$σ(\vec{v})=3$$

                $$σ(\vec{w})=0.5$$

                $$σ(\vec{u})=-1$$

                $$σ(\vec{t})=0$$

        我们发现，上面这条定理可以直观的让我们获取协向量作用在普通向量上的值。这就是为什么我们要把协向量画成那么奇怪的形式。

        接下来我们要干的一件事是定义协向量的两种运算。首先，协向量的数乘运算很简单。一个协向量乘$以n$，就把那个协向量的线条疏密程度增加$n倍$。

        通过协向量的数乘运算，我们可以处理之前遗留下来的问题。如果一个协向量，第二个分量不为一，那么我们可以通过数乘的方法解决。

        假设现在有$协向量μ=[3\ 2]，则：$

                $$μ=[3\ 2]=2[1.5\ 1]$$

        这样的话，我们就可以先$做出[1.5\ 1]$的图像，再把线条的疏密程度增加两倍。

        协向量的加法运算更简单。我们只需要遵循矩阵的加法规则。就是这样。我都懒得再打出来了。

        这么一看，第四课大部分东西都讲完了。只剩一个对偶空间没有讲了。

$\Large{L_{4.5}：对偶空间}$

        我们说，协向量可以把向量空间中的向量映射回实数域。那么我们可不可以把所有的协向量构成一个集合呢？可以。这就是我们要说的对偶空间。

                若$\mathbb{F}上存在赋范空间\mathscr{X}$，那么$从\mathscr{X}到\mathbb{F}$的连续线性映射构成的实巴拿赫空间$称\mathscr{X}$的$\red{对偶向量空间(Dual\ Vector\ Space)}$，简称$\red{对偶空间(Dual\ Space)}$，记$作\mathscr{X}^*$。

        至于这个定义里的那个什么赋范空间，什么巴拿赫空间，什么连续线性映射，通通不用管。我们只需要知道，对偶空间就是向量空间对应的全体协向量构成的集合。$所以，对偶空间V^{*}可以表示$为：

                $$V^*=$${$$φ|φ:V→\mathbb{R}$$}或者{$$φ|φ(\vec{v})=a|\vec{v}∈V|a∈\mathbb{R}$$}

        而且，对偶空间有以下定理：

                 $$V^{**}=V$$

        在对偶空间上定义的加法和数乘满足线性规则：

                $$(1)(nα)(\vec{v})=nα(\vec{v})\quad (n∈\mathbb{R},α∈V^*,\vec{v}∈V)$$

                $$(2)(α+β)(\vec{v})=α(\vec{v})+β(\vec{v})\quad (α,β∈V^*,\vec{v}∈V)$$

         以上就是第四课的全部内容。不过我们对于协向量的学习仍然没有结束。下一课我们将讲述协向量的基，以及协向量为什么是协变量，它是如何变换的。敬请期待！