物理

张量分析入门-L₁:什么是张量？

        好的同学们，欢迎收看张量分析入门的第一节课。

        在我们正式研究张量之前，我们需要知道张量是什么，这也是我们这节课的主题。

$\huge{L_1： 什么是张量？}$

        首先我们给出张量的第一个定义，即为张量的坐标定义。

                $\red{张量(Tensor)是一种数组的统称。}$

        这个定义看起来非常简单，是不是？$比如典型的，三阶单位矩阵I_3$:

                $$I_3=\left[\begin{array}{ccc}1\ 0\ 0\\0\ 1\ 0\\0\ 0\ 1\end{array}\right]$$

        它就是一个张量，对不对？

        对，也错。

        我们在这里说张量是一个数组，其实是不严谨的说法。在上初中语文时候，我们大家都学过说明方法。其中有两个说明方法，一个是作诠释，一个是下定义。这里我们所给出的解释只能算是做诠释，而不是下定义。因为我们把这句话反过来说，会发现这句话是错的。换句话说，这个命题的逆命题是一个否命题。“数组是张量”，如果真是这样，我们学的线性代数，就该改名叫做张量代数了。很显然，这个定义是不完备的。

        那么我们尝试给出张量的第二个定义，坐标定义。

                $\red{张量(Tensor)是一个在坐标系变化下不变的对象，并且具有在坐标系变化下以可预测特殊方式变化的组件。}$

        这有点难懂了，是不是？没关系，我们一个一个来解释。首先在“坐标系变化下不变”是什么意思？我们举一个例子。假设你现在有一支铅笔，这支铅笔指向你家的门。我们随便构建两个$坐标系Oxyz和O'x'y'z'，$我们用这两个坐标来表示这支铅笔。不管我们怎么表示，这个铅笔本身的长度变不变呢？不变。假设我们现在$有一只10cm的$铅笔，换一个坐标系，它不可$能变成11cm。这支$铅笔指向门，换多少个坐标系它，都不可能指向窗户。这就是“坐标系变化下不变”的含义。那么“在坐标系变化下以可预测特殊方式变化”是什么意思呢？为了理解这个词，我们把铅笔视做一个向量。众所周知，向量$在xyz轴上$都有其分量。当我们变换坐标系时，这些分量都会随坐标系的变化而变化。但是我们的后续课程会讲到，这里所说的铅笔是一个逆变向量，它分量的变化可以通过基变换使用的过渡矩阵来预测。这里提前剧透一下，逆变向量的变换使用的是基变换过渡矩阵的逆来进行变化。当然，看不懂没有关系，我们在后续的课程中都会提到。

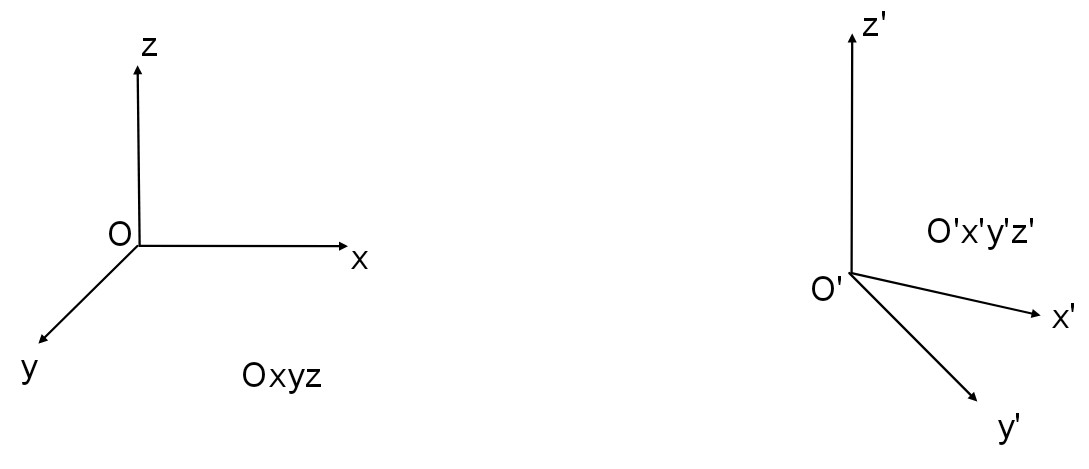
        不过和第一个定义一样，这个定义也是不完备的。这是一个做诠释，而不是一个下定义。

        让我们最后再试一个，给出张量最终的定义，抽象定义。

                $\red{张量(Tensor)是使用张量积将向量和协向量组合起来的集合。}$

        这个定义最终变得很短，也很有用。但是同学们可能听不懂，这很正常。在学习张量之前，你可能听说过向量。但什么是协向量？什么是张量积？没关系，在后续的课程中我们都会提到这些概念。

        现在看来张量远比你想象的要复杂的多，没错吧？

        不用担心，后面的更复杂。